
ΑΙhub.org
Interview with Haggai Maron – #ICML2020 award winner
Haggai Maron, Or Litany, Gal Chechik and Ethan Fetaya received an Outstanding Paper Award at ICML2020 for their work On Learning Sets of Symmetric Elements. Here, lead author Haggai tells us more about their research, how he goes about solving problems, and plans for future work in this area.
What is the topic of the research in your paper?
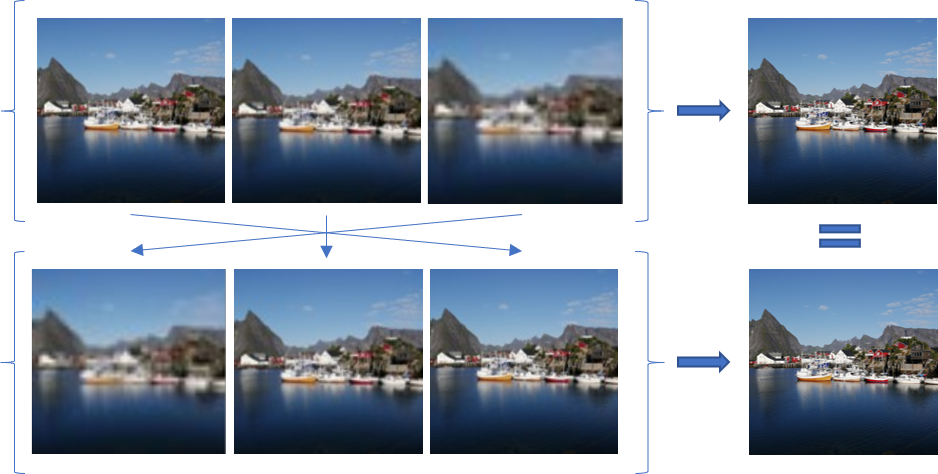
We target learning problems in which the input is a set of images or other structured objects like graphs. The challenge here is building a learning model that does not pay attention to the order of the elements and at the same time respects their structure. For example: imagine you have several photos of a scene on your smartphone, and you want to select a single high-quality photo. The order in which the images were taken is irrelevant. Moreover, as we deal with images we would like to take their structure (a grid of pixels) into account.
Machine learning models, and deep neural networks in particular, can be designed to learn well from images because we understand what they can ignore: the precise position of objects. An image of a cat should still be classified as “cat” even if it is shifted a few pixels to the left. Similarly, a set of photos is still the same set, even if we shuffle their order. This property, where something appears the same across different views, is known in mathematical terms as Symmetry.
One example problem we tried to solve is to identify the best image in an unordered photo collection of the same scene. There are two types of symmetries in this problem: First, the best image should be selected regardless of the collection order. Second, the best image should be selected even if the location of key elements has shifted slightly.
As it turns out, similar structures are present when working with sets of sounds, signals, images, 3D point-clouds and even graphs. In all of these cases the elements are ordered arbitrarily, and each element has a special symmetric structure. Also, selection is just one type of application. Other very important applications, which we also demonstrate in our work, include reconstruction of 3D data from multiple views, and image enhancement.
Could you tell us a little bit about the implications of your research and why it is an interesting area for study?
Our paper has both theoretical and practical implications. Practically, our research is relevant to numerous applications, from creating a high-quality image by removing noise and blur due to camera shake (deblurring images) to multi-camera view for 3D shape identification and reconstruction, e.g. autonomous driving applications. Theoretically, our results strengthen our understanding of the approximation power of equivariant and invariant neural networks, and answered several open questions regarding earlier models.
Could you explain your methodology?
I tackle problems with a mathematically based approach. I first define the problem in a rigorous way and then try to derive the algorithm from first principles. I also strive to provide theoretical guarantees for the suggested algorithms. In the specific case of this paper, we first formulated the mathematical structure of our data (a set of structured elements) and then derived the neural network layers by characterizing the space linear equivariant layers, which are an analog to the well-known convolutional layers used for images. We also provide theoretical guarantees in the form of an analysis of the approximation power of neural networks that are composed of these layers.
What were your main findings?
Our paper investigates both the theoretical and practical aspects of the learning setup mentioned above. As deep neural networks can assume many different architectures, it is first crucial to specify which architecture best fits this structure with multiple symmetries. We first identify which architecture of deep networks should be used in these cases. This generalizes previous works that focus on a specific task and domain, into a general framework that works on multiple problems and across various domains. We further show that our architecture has maximal expressive power within the class of functions we are interested in. Surprisingly, our architecture is extremely easy to implement, and can be easily integrated with existing network architectures.
What further work are you planning in this area?
There are many exciting directions for future work. On the practical side, we wish to apply our architecture to problems from many different fields such as audio analysis and computer vision. On the theoretical side, there are still several important questions in this field that are still open. For example, understanding approximation and generalization in general invariant neural networks is an important goal.
Read the paper in full: On Learning Sets of Symmetric Elements, Haggai Maron, Or Litany, Gal Chechik, Ethan Fetaya
About the author

Haggai Maron
Haggai Maron joined Nvidia Research in October 2019 as a research scientist. His main fields of interest are machine learning and shape analysis, with a focus on applying deep learning to irregular domains (e.g., sets, graphs, point clouds, and surfaces) and graph/shape matching problems. Haggai completed his MS and PhD at the Department of Computer Science and Applied Mathematics at the Weizmann Institute of Science, and his BS in mathematics and computer science from the Hebrew University of Jerusalem.
tags: ICML, ICML2020










