Investigating neural collapse in deep classification networks

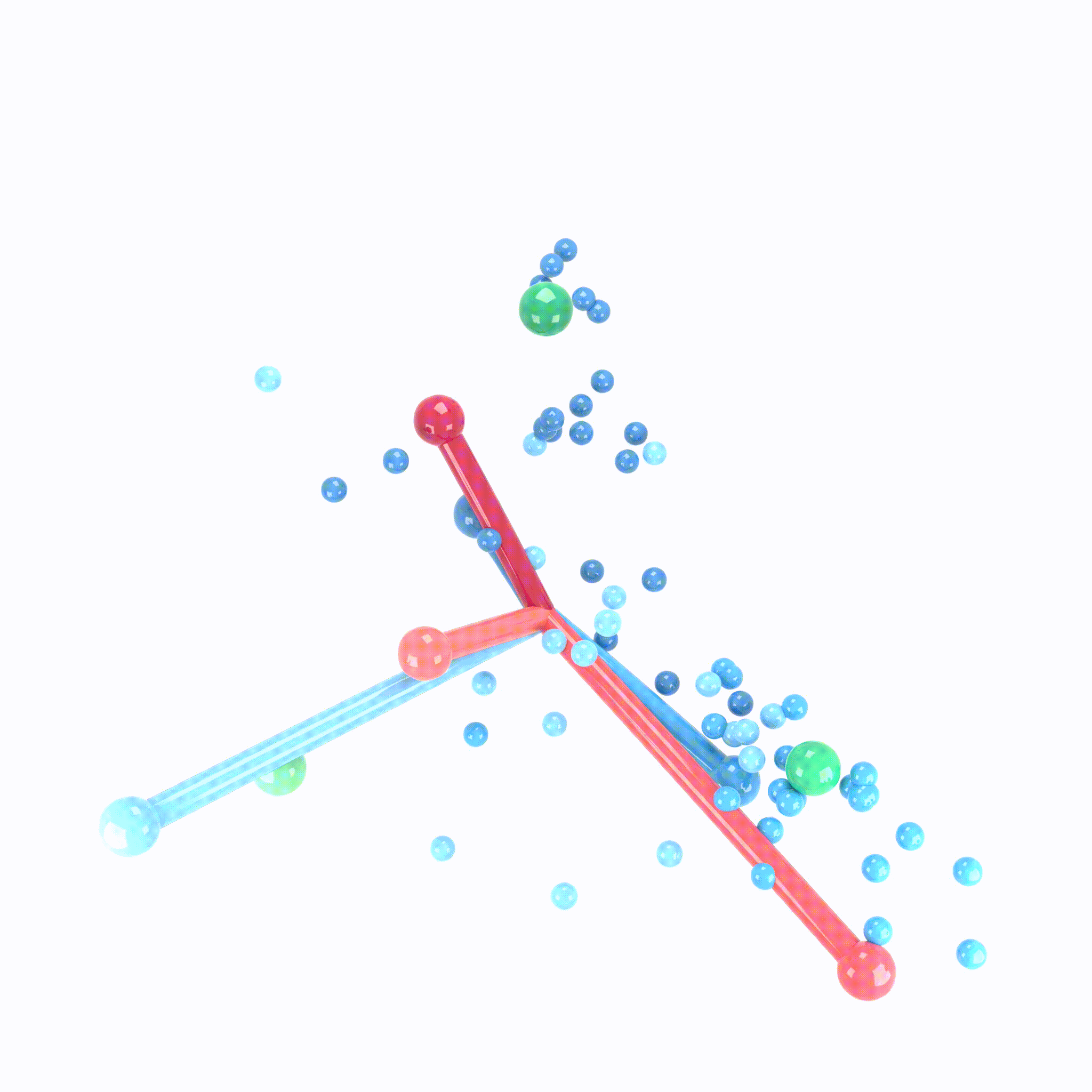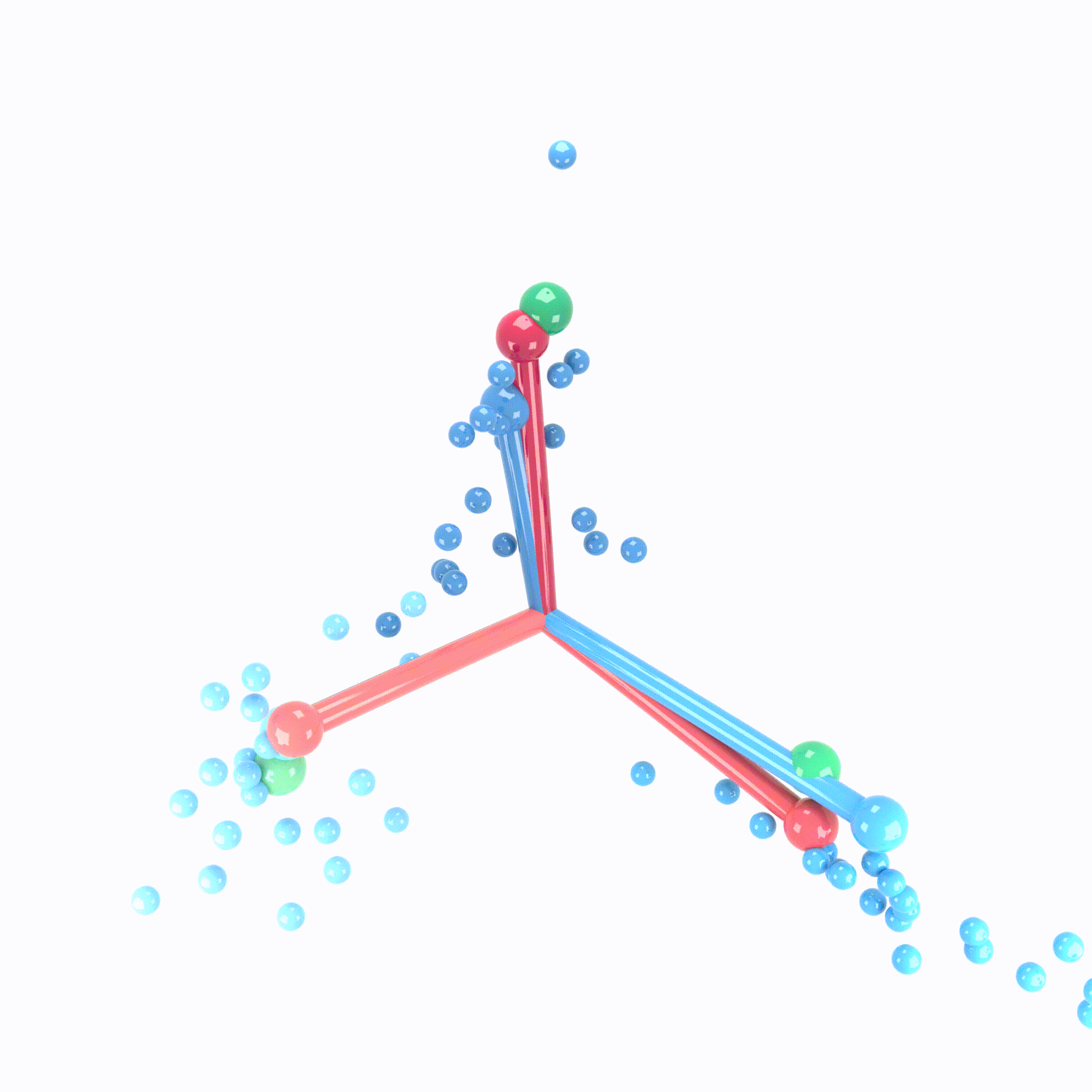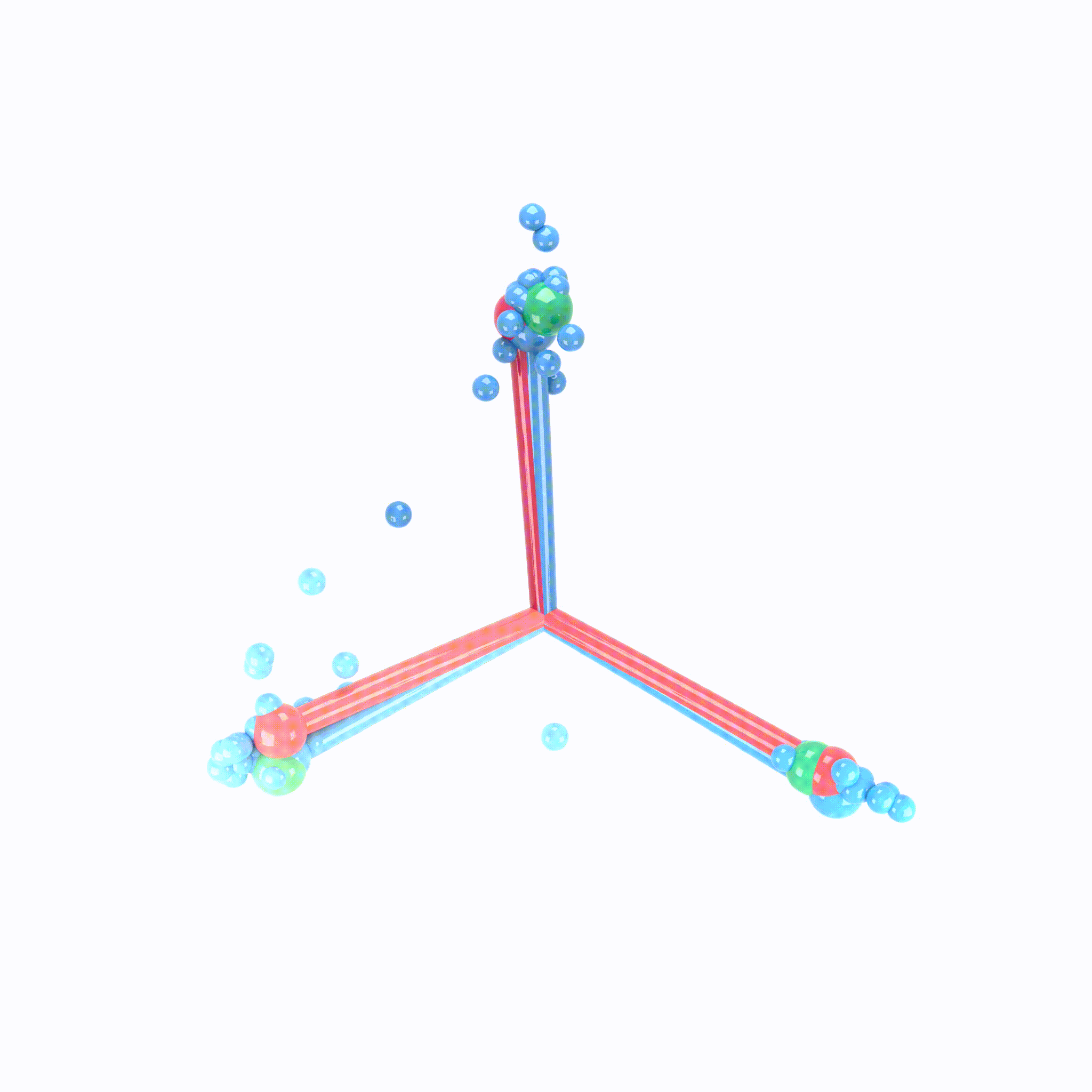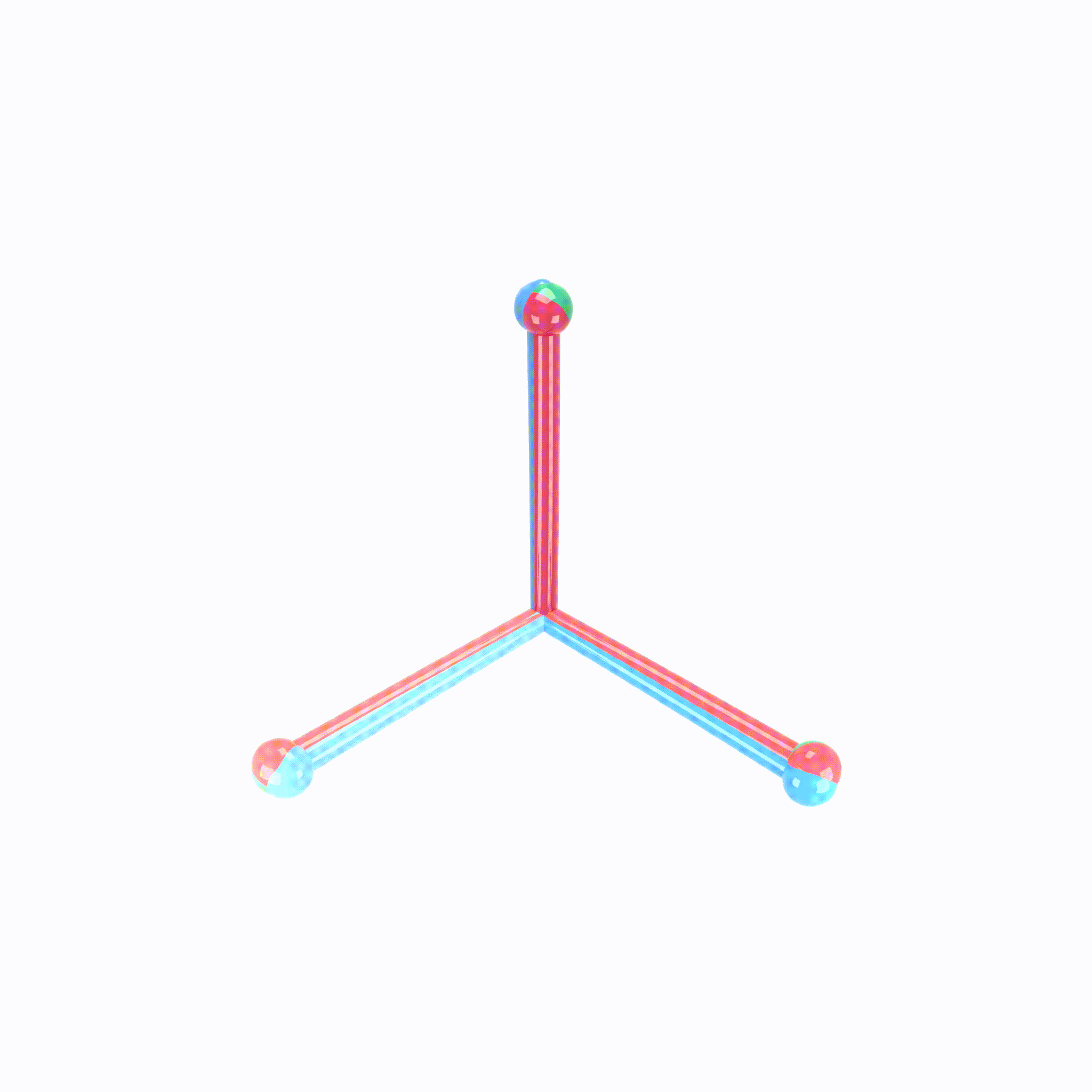Animation demonstrating the neural collapse phenomenon. Credit: X.Y. Han, Vardan Papyan, and David Donoho.

X.Y. Han, Vardan Papyan, and David Donoho won an outstanding paper award at ICLR 2022 for their paper Neural collapse under MSE loss: proximity to and dynamics on the central path. Here, they tell us more about this research, their methodology, and what the implications of this work are.

What is the topic of the research in your paper?

Our work takes a data scientific approach to understanding deep neural networks. We make scientific measurements that identify common, prevalent empirical phenomena that occur in canonical deep classification networks trained with paradigmatic methods. We then build and analyze a mathematical model to understand the phenomena.

What were your main findings?

When making measurements on canonical deep net architectures trained with paradigmatic practices, we observed an interesting behavior of the penultimate deep net layer: the features collapse to their class-means, both classifiers and class-means collapse to the same Simplex Equiangular Tight Frame, and classifier behavior collapses to the nearest-class-mean decision rule. We call this behavior “Neural Collapse”. In this paper, we derive the dynamics of Neural Collapse in explicit form under a popular mathematical model for deep nets.

Could you tell us about the implications of your research and why it is an interesting area for study?

Because of the complexity of modern deep nets, practitioners and researchers still regard them as mostly opaque, but highly-performing boxes. These opaque boxes are massively over parameterized and researchers frequently engineer new adjustments to improve their performance. Thus, one might expect the trained networks to exhibit many particularities that make it impossible to find any empirical regularities across a wide range of datasets and architectures. Our findings are interesting because—on the contrary—we reveal that Neural Collapse is a common empirical pattern across many classification datasets and architectures. Careful theoretical analysis of this pattern and its limiting equiangular tight frame (ETF) structure can give insights into important components of the modern deep learning training paradigm such as adversarial robustness and generalization.

Could you explain your methodology?

Building upon a previous work where we demonstrated Neural Collapse on the cross-entropy loss, in this work, we first establish the empirical reality of Neural Collapse on mean squared error (MSE) loss by demonstrating its occurrence on three canonical networks and five benchmark datasets. We then exhibit a new set of experiments showing that the last-layer classifiers stay “least-squares optimal” relative to its associated features roughly at any fixed point in time. When classifiers and features satisfy this correspondence, we say they are on a “central path”.

The simple analytic form of the MSE loss allows us to perform deeper mathematical analyses of training dynamics leading to Neural Collapse than is currently possible on cross-entropy. In particular, by adopting the popular “unconstrained features” (or “layer-peeled”) model, we derive explicit, closed-form dynamics of Neural Collapse on the central path.

What further work are you planning in this area?

We are interested in examining the implications of Neural Collapse for generalization. As we describe in an “Open Questions” section of this paper, we do empirically observe the occurrence of Neural Collapse on test data as well, but at a much slower rate. In future works, we hope to show more extensive measurements characterizing Neural Collapse on out-of-sample data and leveraging these observations towards predicting a deep net’s test performance and adversarial robustness.

References

Vardan Papyan, X.Y. Han, and David L. Donoho. Prevalence of neural collapse during the terminal phase of deep learning training. Proceedings of the National Academy of Sciences (PNAS), 117.40 (2020): 24652-24663.

X.Y. Han, Vardan Papyan, and David L. Donoho. Neural collapse under MSE loss: proximity to and dynamics on the central path. International Conference on Learning Representations (ICLR) 2022.

X.Y. Han is a PhD Candidate in the School of Operations Research and Information Engineering at Cornell University. He earned a BSE in Operations Research and Financial Engineering from Princeton University in 2016 and a MS in Statistics from Stanford University in 2018.

Vardan Papyan is an assistant professor in Mathematics, cross-appointed with Computer Science, at the University of Toronto, affiliated with the Vector Institute for Artificial Intelligence and the Schwartz Reisman Institute for Technology and Society. His research spans deep learning, signal processing, high-performance computing, high-dimensional statistics, and applied mathematics. His research was recognized by the Natural Sciences and Engineering Research Council in Canada through a Discovery Grant and a Discovery Launch Supplement and by Compute Canada.

David Donoho is the Anne T. and Robert M. Bass Professor of Humanities and Sciences and a professor in the Department of Statistics at Stanford University.

AIhub is dedicated to free high-quality information about AI.

AIhub is dedicated to free high-quality information about AI.