
ΑΙhub.org
Mitigating biases in machine learning
Machine Learning (ML) is increasingly being used to simplify and automate a number of important computational tasks in modern society. From the disbursement of bank loans to job application screenings, these computer systems streamline several processes that have a considerable impact on our day to day lives. However, these artificially intelligent systems are most often devised to emulate human decision making — an inherently biased framework. For example, Microsoft’s Tay online chatbot quickly learned to tweet using racial slurs as a result of the biased online input stream (Caton and Haas 2020), and the COMPAS tool often flagged black individuals as more likely to commit a crime (even if two individuals were statistically similar with respect to many other attributes) (Flores, Bechtel and Lowenkamp 2016).
Crucially, these issues are not the product of a malevolent computer programmer instilling radical beliefs, but rather a byproduct of machines learning to optimize for a particular objective, which can inadvertently leverage underlying biases present in the data. These biases are most often the result of two (not mutually exclusive) pervasive issues in data science: bad training data and objectives that are blind to demographic (or comparable sensitive information) considerations. The former is nicely depicted again by the Tay chatbot: training on text from anonymous online forums is unfortunately not a good representation of how the general population talks. Additionally, when models are trained to optimize for an objective that ignores demographic considerations, discriminatory practices can inadvertently be learned, as was the case for the COMPAS algorithm. The algorithm was trained to predict future criminal behavior but inadvertently learned to weigh an individual’s race heavily in its decision-making process.
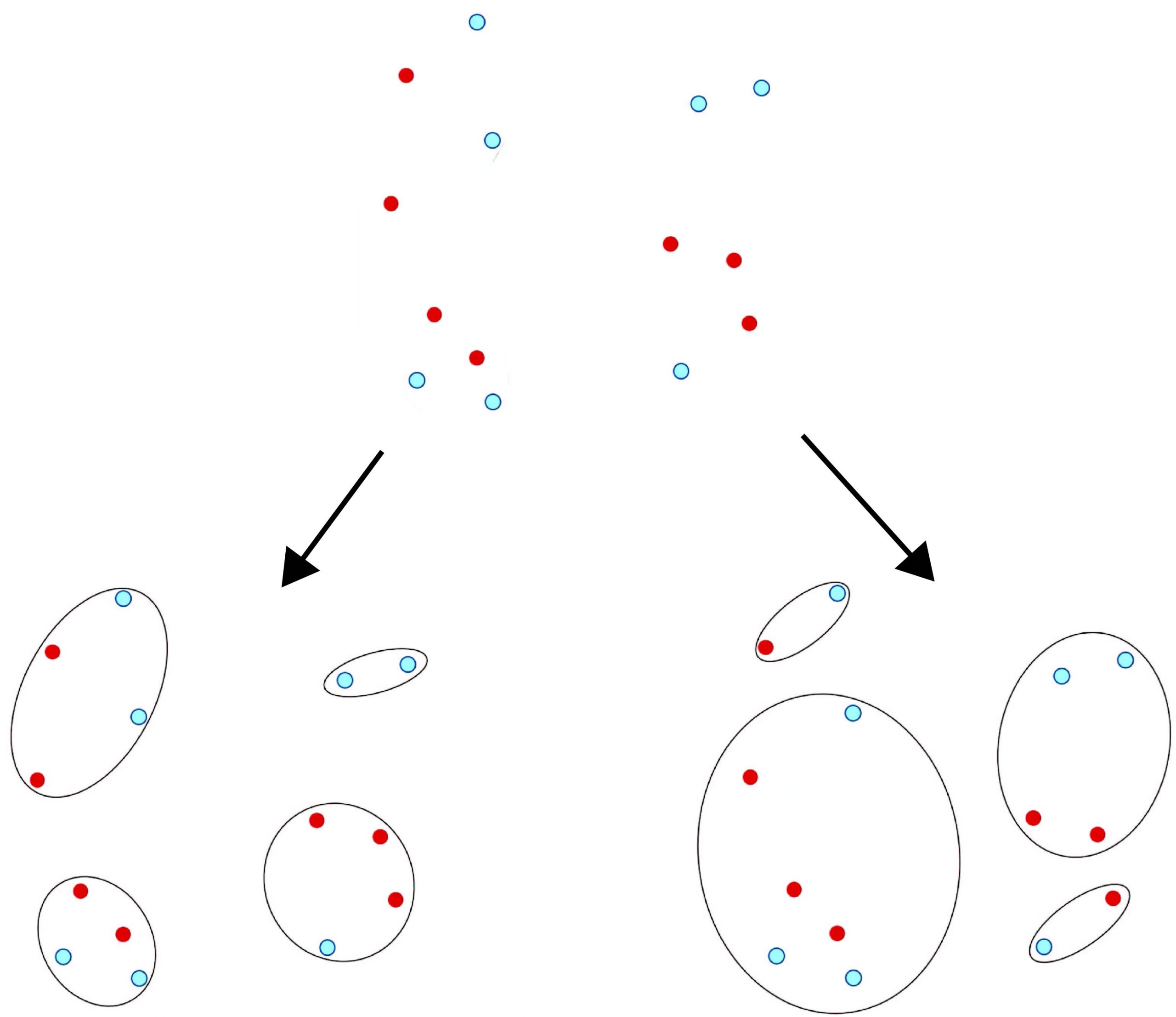
To provide a clearer understanding of how these “blind” objectives work, we here restrict our attention to the process of clustering data. This involves grouping objects so that those in the same cluster are more like each other than those in other clusters. Data scientists use cluster analysis to garner insight from data by merely observing which cluster a point belongs to and assuming it shares the typical properties of that group. For instance, if we represent a patient’s medical data as a set of relevant numbers such as height, weight, and age, we can visualize the data as points in a three-dimensional space. We can then use standard methods to cluster the data by identifying data points that are close together in this space. To do this, we minimize an “objective function” that measures this closeness. However, this process may inadvertently segregate men from women, as these groups are likely to be similar in terms of height and weight. This is a toy example of the inherent biases that clustering algorithms learn which can have a significant impact on the treatment that a physician provides if not recognized.
While under-representative data has a (somewhat) clean solution in improved collection procedures, mitigating bias as a result of objective minimization is less clear. In an effort to counteract this issue, researchers have recently turned to propose algorithms that ensure some quantified form of “fair representation” at the cost of a degradation in the optimality of a clustering. Consider the following figure that depicts a traditional clustering result versus what one would deem “fair”, where the two colors are representative of some protected attribute such as gender or race. We see that the standard (blind) solution may yield clusters of data points that disproportionately segregate the data based on an implicit attribute, leading to potentially discriminatory or even illegal behavior by the algorithm. A more desirable solution in practice might yield clusters that contain equal representation of the two protected attributes while also mitigating the intra-cluster distances between data points.

In essence, balancing solutions that minimize our objective with those that yield equal representation is the crux of modern fair clustering work. While in the past few years a considerable number of studies have examined fair flat clustering (partition data into disjoint clusters), the major problem of hierarchical clustering has been largely neglected. Like the flat variant depicted above, hierarchical starts with a collection of data points whose similarity is measured as the distance between points — the closer two points are, the more similar. Now to build a hierarchy, we first let each point be its own cluster and subsequently merge these with neighboring clusters up to a certain size. We can then repeat this process on our enlarged groupings until we are left with one that encompasses all our data. A major advantage here is that we do not need to impose a restriction on the number of clusters on the data, rather we try to group things at a wide variety of granularities. For this reason, hierarchical clustering is common in the division of a geographic region or for phylogenetic trees.
In our recent work (Knittel et al. 2023), we examine the notion of fairness in hierarchical clustering due to its pervasive utility in data science. Specifically, we demonstrate that a relatively intuitive algorithm that strategically folds clusters onto one another according to their protected attribute representations can produce a fair clustering with only a modest decrease in the optimality of the solution (as measured by the objective function). Such results are highly nontrivial as well as vital to demonstrating the utility of fairness constraints.
Although technological innovation is accelerating daily, it is important to be cognizant of, and mitigate, potentially harmful algorithmic practices that can perpetuate biases. We hope that our work serves as further proof of concept that incorporating fairness constraints or demographic information into the optimization process can reduce biases in ML models without significantly sacrificing performance – a result that is critical where automated decision-making can have a harmful impact.
References
- Fairness in Machine Learning: A Survey, Simon Caton and Christian Haas, arXiv 2020.
- False positive, false negatives, and false analyses: A rejoinder to machine bias: There’s software used across the country to predict future criminals, and it’s biased against blacks, Anthony W Flores, Kristin Bechtel and Christopher T Lowenkamp, Federal Probation, 2016.
- Generalized Reductions: Making any Hierarchical Clustering Fair and Balanced with Low Cost, Marina Knittel, Max Springer, John P Dickerson, and Mohammad Taghi Hajiaghayi, arXiv 2023.










