ΑΙhub.org
#IJCAI2023 distinguished paper – Safe reinforcement learning via probabilistic logic shields
Image created by author using DALL.E. Prompt: “A woman getting into a self driving car. Cartoon style”
Are you excited about self-driving cars? Would you trust autonomous driving technology if you were invited to step into a self-driving vehicle? Most importantly, how do you know whether you would be safe during the journey?
Safety is difficult to measure, unlike accuracy, which we are more familiar with. It often feels awkward to describe safety using accuracy-related terms, such as “99 out of 100 journeys are safe” or “99.5% of pedestrians on the roads are correctly identified.“ Hearing this immediately makes us think – what happened on that one trip? Did somebody get injured? What happened to the 0.5% of pedestrians that did not get identified? How confident is the vehicle when it identifies a pedestrian? Does the behavior of the vehicle change when it is only 50% sure that there is a pedestrian compared to when it is 90% sure? The vehicle should brake harder for a 90% certainty than for a 10% certainty, right?
Also, how does the model find a trade-off between safety and the other criteria? Driving at 5 km/hr is safe most of the time, but the passenger most likely wants to reach their destination as soon as possible.
These questions are at the core of safety in AI. Understanding how a machine learning model learns and reasons is crucial to making technologies more trustworthy.
Our paper provides a framework to represent, quantify, and evaluate safety. We define safety using a logic-based approach rather than a numerical one, thus enabling efficient training of safe-by-construction deep reinforcement learning policies. Our approach is a variant of a “shield” but has several advantages compared to a traditional one, including:
- Our approach better integrates with continuous, end-to-end deep RL methods.
- Our approach efficiently utilizes the inherent noise and uncertainty in the unstructured input (e.g. images).
- Our approach can be seamlessly applied to any policy gradient algorithm.
- Our approach finds a better trade-off between the traditional RL objective and the safety objective.
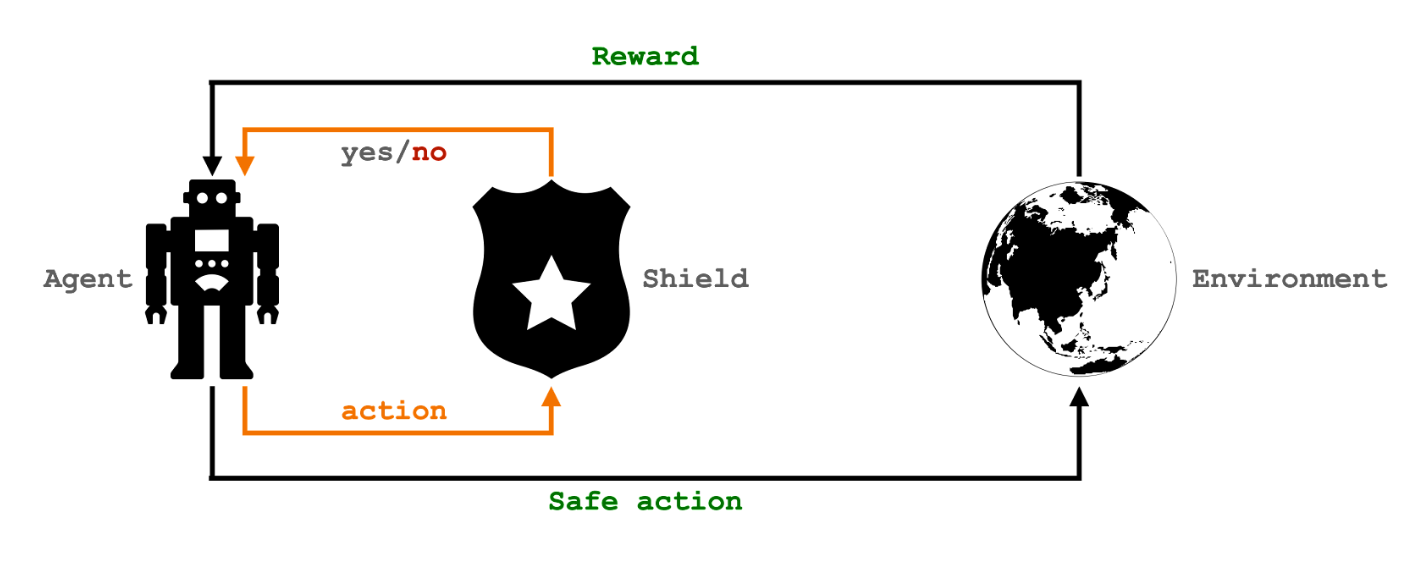
Shielding is a popular Safe Reinforcement Learning (Safe RL) technique that aims to find an optimal policy whilst making sure that the agent stays safe. To do so, it relies on a shield, a logical component that monitors the agent’s actions and rejects those that violate the given safety constraint. Before the agent performs an action, it consults the shield whether the action it wants to perform is safe or not.
We will now introduce a running example, illustrate our approach, and then compare it to the more traditional methods.
Running example
Image created by author using DALL.E. Prompt: “Car driving in a city through an intersection. There is a car in front and another on the right. A wide view from the front window.”
Consider a self-driving agent in the figure above that encounters a red light and another vehicle to its right. The agent is equipped with a standard neural policy that takes the image as input and produces a policy, i.e. a probabilistic distribution over five predefined actions {do-nothing, accelerate, brake, turn-left, turn-right}. An example policy can be:
π(do-nothing)=0.1, π(accelerate)=0.5, π(brake)=0.1, π(turn-left)=0.1, π(turn-right)=0.2
The shield has a set of sensors to detect from the image whether there is an obstacle (i.e., the red light and the other car) in front, on the left or on the right of the agent.
P(obs_front)=0.8, P(obs_left)=0.2, P(obs_right)=0.5
The shield has safety-related knowledge represented by a set of probabilistic if-else statements. The first rule below states “if there is an obstacle in the front, and the agent accelerates, then a crash will occur with a probability of 0.9.”
0.9::crash :- obs_front, accelerate.
0.4::crash :- obs_left, turn-left.
0.4::crash :- obs_right, turn-right.
The shield defines safety as the probability of not having a crash, i.e. P(safe) = 1-P(crash).
Now, our goal is to modify the given policy π so that it becomes safer.
Our Approach
Given the above information, our approach consists of three steps.
- Action safety P(safe|a): how safe will the agent be if it executes an action a?
- Policy safety Pπ(safe): how safe will the agent be if it randomly selects an action using a policy π
- By combining the two components above, we can then make the policy π safer. The improved, safer policy is denoted by π+ and π+ is guaranteed to be safer than π. This is key to improving the safety of the entire learning process.
The following table illustrates the three steps. The last column shows the improved policy that the agent will use to sample an action to execute in the environment. We will now explain how these values are calculated.
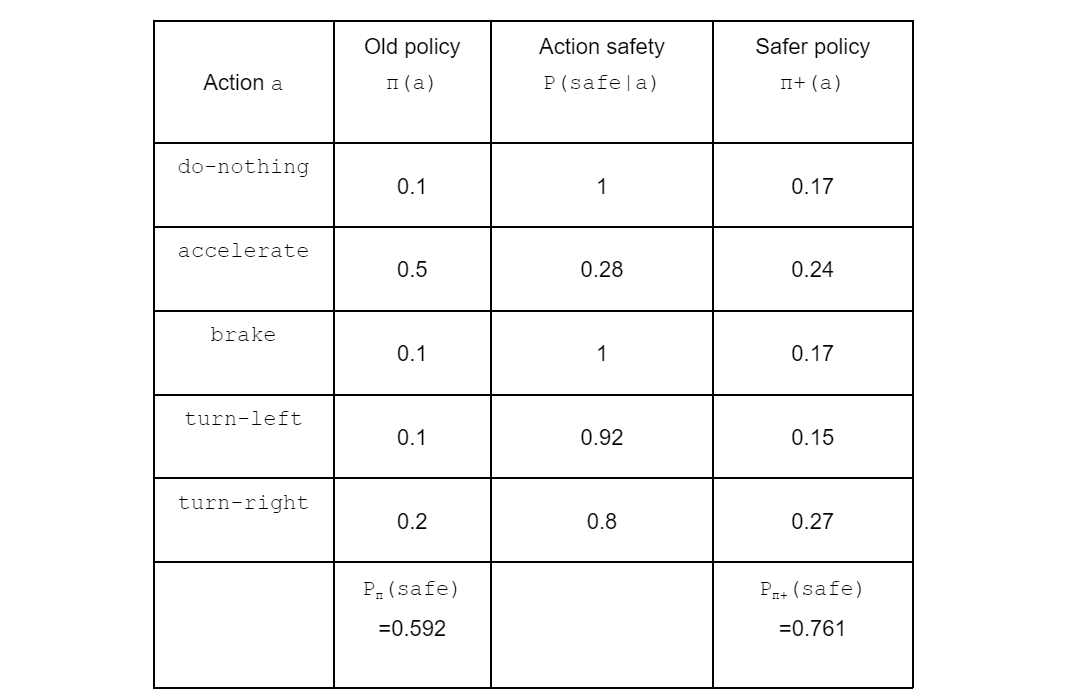
Action safety
The first step is to quantify how safe it is to take an action. This can be easily computed using the if-else statement. For example, 0.9::crash :- obs_front, accelerate and P(obs_front)=0.8 together infer that the probability of having a crash if the agent decides to accelerate is P(crash|accelerate)=P(obs_front)*0.9 = 0.72. Then, the probability of staying safe if the agent accelerates is simply P(safe|accelerate) = 1- P(crash|accelerate)= 0.28.
Policy safety
The second step is to compute how safe it is to follow a given policy. This is defined as the average of each action safety weighted by their probability, denoted by Pπ(safe). In our running example, Pπ(safe) = 1*0.1+0.28*0.5+1*0.1+0.92*0.1+0.8*0.2 = 0.592.
Making the policy safer
Finally, we now would like to increase the probability of selecting safe actions and decrease the probability of selecting unsafe ones. To do this, we compute a coefficient P(safe|a)/Pπ(safe) indicating how safe an action a is compared to the other actions. If the action a is relatively safe, the coefficient should be larger than one. Otherwise, it is smaller than one. For example, P(safe|accelerate)/Pπ(safe)=0.28/0.592=0.47, indicating that accelerate is relatively unsafe.
Then, we can multiply the coefficient with the original π(a) to obtain a safer policy, i.e. π+(a). In our running example, π+(accelerate)=0.24, which is lower than the original value 0.5. As a result of this mechanism, the new policy is guaranteed to be safer than the original policy. By using the new policy instead of the old policy, the learning process will be safer.
Comparison with other approaches
We evaluate our approach using Atari games where the agent must select one of the several discrete actions (e.g. accelerate, turn-left, etc) to finish an episodic task such as driving along a road as fast as possible. The agent also has a safety objective such as not driving away from the road.
We compare our approach to two baselines and analyze their behavior.
- Standard deep RL is the baseline that does not consider the safety objective. This agent generally takes much risk, e.g. making hard turns to reach the destination sooner.
- Traditional Shields are similar to our approach but assume that any action is either safe or unsafe, i.e. P(safe|a)=0 or 1. This agent is safer than the standard RL agent but may not be more rewarding as it takes no risks.
- Our approach finds the best trade-off between the reward and the safety objectives. This agent is the safest and most rewarding among all agents.
We have introduced a novel class of shields that enable efficient training of safe-by-construction neural policies. It is a probabilistic generalization of traditional shields. Future work will be dedicated to extending the current approach to be compatible with a larger class of RL algorithms, including those that employ continuous policies.
Wen-Chi Yang, and colleagues Giuseppe Marra, Gavin Rens and Luc De Raedt, won a IJCAI2023 distinguished paper award for their work: Safe Reinforcement Learning via Probabilistic Logic Shields. You can read the paper in full here.
tags: IJCAI2023
AIhub is supported by:
