Learning programs with numerical reasoning

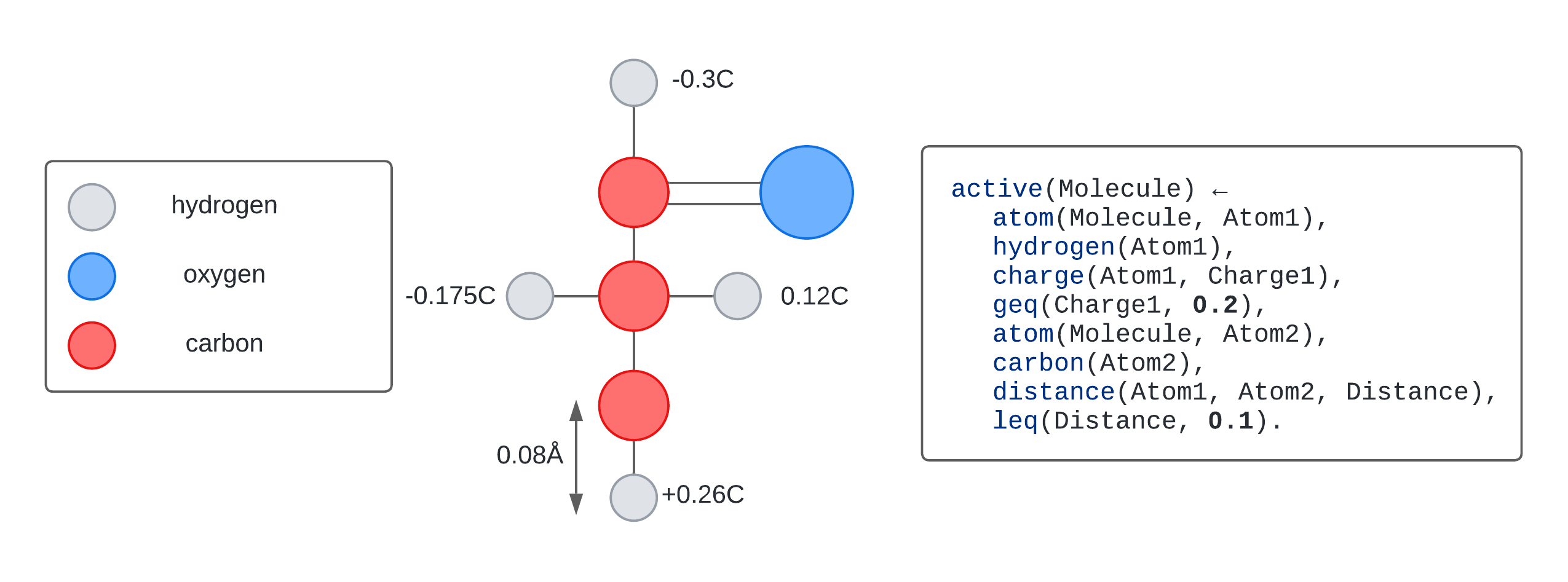
Drug design is the process of identifying molecules responsible for medicinal activity. Suppose we want to automate drug design with machine learning. To do so, we would like to automatically learn programs which explain why a molecule is active or inactive. For instance, as illustrated in the figure above, a program might determine that a molecule is active if it contains a hydrogen atom with a charge greater than 0.2C, and located within 0.1 angstroms of a carbon atom. Discovering this program involves identifying the numerical values 0.2 and 0.1.

To learn such programs for drug design, we need an approach that can generalise from a small number of examples, and that can derive explainable programs characterising the properties of molecules and the relationships between their atoms.

Program synthesis is the automatic generation of computer programs from examples. Inductive logic programming (ILP) is a form of program synthesis that can learn explainable programs from small numbers of examples. Existing ILP techniques could, for instance, learn programs for simple drug design problems.

However, current ILP approaches struggle to learn programs with numerical values such as the one presented above. The main difficulty is that numerical values often have a large, potentially infinite domain, such as the set of real numbers. Most approaches rely on enumerating candidate numerical values, which is infeasible in large domains. Furthermore, identifying numerical values often requires complex numerical reasoning, such as solving systems of equations and inequalities. Current approaches execute programs independently on each example, and therefore cannot reason over multiple examples jointly. As a result, current approaches have difficulties determining thresholds, such as the charge of an atom exceeding a particular numerical value.

In this work, we introduce a novel approach to efficiently learn programs with numerical values [1]. The key idea of our approach is to decompose the learning process into two stages: (i) the search for a program, and (ii) the search for numerical values. In the program search stage, our learner generates partial programs with variables in place of numerical symbols. In the numerical search stage, the learner searches for values to assign to these numerical variables using the training examples. We encode this search for numerical values as a satisfiability modulo theories formula and use numerical solvers to efficiently find numerical values in potentially infinite domains.

Our approach can learn programs with numerical values which require reasoning across multiple examples within linear arithmetic fragments and infinite domains. For instance, it can learn that the sum of two variables is less than a particular numerical value. Our approach learns complex programs, including recursive and optimal programs. Unlike existing approaches, our approach does not rely on enumeration of all constant symbols but only considers candidate constant values which can be obtained from the examples [2], and therefore yields superior performance.

This work is a step forward towards unifying relational and numerical reasoning for program synthesis, opening up numerous applications where learning programs with numerical values is essential.

References

[1] C. Hocquette, A. Cropper, Relational program synthesis with numerical reasoning, AAAI, 2023.
[2] C. Hocquette, A. Cropper, Learning programs with magic values, Machine Learning, 2023.

Our code can be found here.

Céline Hocquette is a researcher at the University of Oxford.

Céline Hocquette is a researcher at the University of Oxford.