
ΑΙhub.org
In defense of weight-sharing for neural architecture search: an optimization perspective
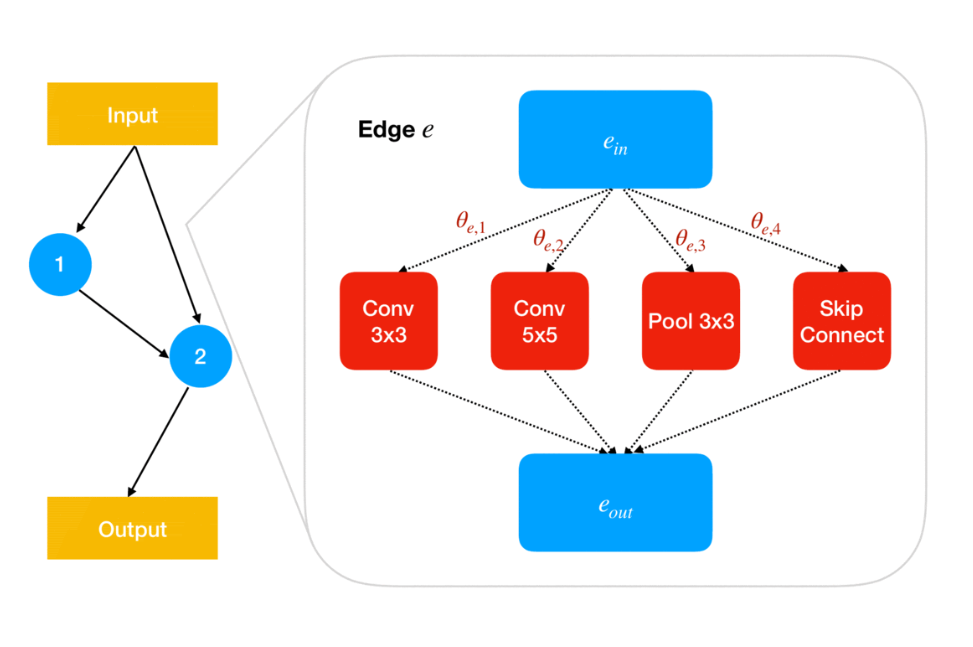
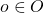 to an edge
to an edge  with a
with a 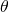 -weighted combination of their outputs. At each edge
-weighted combination of their outputs. At each edge  in the network, the value at input node
in the network, the value at input node 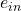 is passed to each operation in O={1:Conv 3×3, 2:Conv 5×5, 3:Pool 3×3, 4:Skip Connect}; the value at output node
is passed to each operation in O={1:Conv 3×3, 2:Conv 5×5, 3:Pool 3×3, 4:Skip Connect}; the value at output node 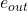 will then be the sum of the operation outputs weighted by parameters
will then be the sum of the operation outputs weighted by parameters ![Rendered by QuickLaTeX.com \theta_{e,o}\in[0,1]](https://aihub.org/wp-content/ql-cache/quicklatex.com-6c6f47ff2916fd890371b7ef131779fe_l3.png) that satisfy
that satisfy 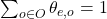 .
.By Misha Khodak and Liam Li
Neural architecture search (NAS) — selecting which neural model to use for your learning problem — is a promising but computationally expensive direction for automating and democratizing machine learning. The weight-sharing method, whose initial success at dramatically accelerating NAS surprised many in the field, has come under scrutiny due to its poor performance as a surrogate for full model-training (a miscorrelation problem known as rank disorder) and inconsistent results on recent benchmarks. In this post, we give a quick overview of weight-sharing and argue in favor of its continued use for NAS. To do so, we will consider a simple optimization formulation that reveals the following key takeaways:
- The fact that weight-sharing works should not really be too surprising to a community that embraces non-convex optimization of over-parameterized models.
- Rank disorder is not a concern for most weight-sharing methods, since we care about obtaining high-quality architectures rather than a ranking of them.
- The sometimes-poor performance of weight-sharing is a result of optimization issues that can be fixed while still using weight-sharing. We propose such a fix — a geometry-aware exponentiated algorithm (GAEA) — that is applicable to many popular NAS methods and achieves state-of-the-art results across several settings.
A brief history of NAS with weight-sharing
NAS is usually formulated as a bilevel optimization problem in which we are searching over some architecture domain ![]() for the architecture
for the architecture ![]() that achieves the lowest validation loss
that achieves the lowest validation loss ![]() after training weights
after training weights ![]() that minimize the training loss
that minimize the training loss ![]() :
:
![]()
First-generation NAS methods were astronomically expensive due to the combinatorially large search space, requiring the training of thousands of neural networks to completion. Then, in their 2018 ENAS (for Efficient NAS) paper, Pham et al. introduced the idea of weight-sharing, in which only one shared set of model parameters ![]() is trained for all architectures. The validation losses
is trained for all architectures. The validation losses ![]() of different architectures
of different architectures ![]() computed using these shared weights are then used as estimates of their validation losses
computed using these shared weights are then used as estimates of their validation losses ![]() using standalone weights
using standalone weights ![]() (i.e. weights trained individually for each architecture by solving the inner optimization problem above). Because only one set of parameters has to be trained, weight-sharing led to a massive speedup over earlier methods, reducing search time on CIFAR-10 from 2,000-20,000 GPU-hours to just 16. Of great surprise to many was that the validation accuracies
(i.e. weights trained individually for each architecture by solving the inner optimization problem above). Because only one set of parameters has to be trained, weight-sharing led to a massive speedup over earlier methods, reducing search time on CIFAR-10 from 2,000-20,000 GPU-hours to just 16. Of great surprise to many was that the validation accuracies ![]() computed using shared weights
computed using shared weights ![]() were sufficiently good surrogates for
were sufficiently good surrogates for ![]() , meaning ENAS was able to find good models cheaply. We will see that this correlation is actually a sufficient but not necessary condition for weight-sharing to do well and that weight-sharing’s overall success is less surprising than initially thought.
, meaning ENAS was able to find good models cheaply. We will see that this correlation is actually a sufficient but not necessary condition for weight-sharing to do well and that weight-sharing’s overall success is less surprising than initially thought.
Following the ENAS breakthrough, several simpler methods such as DARTS and GDAS were proposed in which the categorical architecture decisions (e.g. for each network edge ![]() , which of some fixed set of operations
, which of some fixed set of operations ![]() to use at
to use at ![]() ) are relaxed into continuous parameters
) are relaxed into continuous parameters ![]() (e.g. so
(e.g. so ![]() is a product of
is a product of ![]() simplices of size
simplices of size ![]() ). As animated in Figure 1, these architecture parameters govern the architecture used for updating the shared weights using the gradient of the training loss; for example, in DARTS,
). As animated in Figure 1, these architecture parameters govern the architecture used for updating the shared weights using the gradient of the training loss; for example, in DARTS, ![]() determines the weighting in the weighted sum of operations output by edge
determines the weighting in the weighted sum of operations output by edge ![]() in the network. Together, this parameterization leads to a continuous relaxation of the earlier bilevel problem:
in the network. Together, this parameterization leads to a continuous relaxation of the earlier bilevel problem:
![]()
Since ![]() is a constrained subset of
is a constrained subset of ![]() , DARTS and GDAS avoid simplex projections by instead re-parameterizing to “logit” parameters
, DARTS and GDAS avoid simplex projections by instead re-parameterizing to “logit” parameters ![]() , with
, with ![]() defined as
defined as
![]()
The relaxed optimization problem can then be approximated via the following alternating gradient update scheme (here ![]() is a stepsize):
is a stepsize):
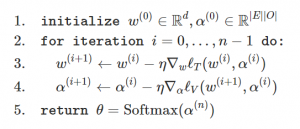
Note that at the end of search, we need to recover a discrete architecture ![]() from the architecture weights
from the architecture weights ![]() ; in DARTS this is done in a pruning step that simply chooses the highest-weighted operations. This post-hoc pruning is a source of error that our method, GAEA, ameliorates, as we discuss later.
; in DARTS this is done in a pruning step that simply chooses the highest-weighted operations. This post-hoc pruning is a source of error that our method, GAEA, ameliorates, as we discuss later.
A further simplification, and perhaps the most striking example of using shared weights as surrogates for standalone weights, is the Random Search with Weight-Sharing (RS-WS) method, in which the shared parameters are optimized by taking gradient steps using architectures sampled uniformly at random from the search space. Despite not even updating architecture parameters, RS-WS achieved competitive and, in some cases, state-of-the-art results.
Should we be using weight-sharing?
More recently, weight-sharing has come under increased scrutiny: does sharing weights between models really accelerate NAS? Can it preclude the recovery of optimal architectures? In particular, several papers have observed the issue of rank disorder, which is when the shared-weight performance of architectures does not correlate well with their stand-alone performance; this issue is illustrated in the figure below. Rank disorder is a problem for methods such as RS-WS that rely on the shared-weights performance to rank architectures for evaluation, as it will cause them to ignore networks that achieve high accuracy when their parameters are trained without sharing.
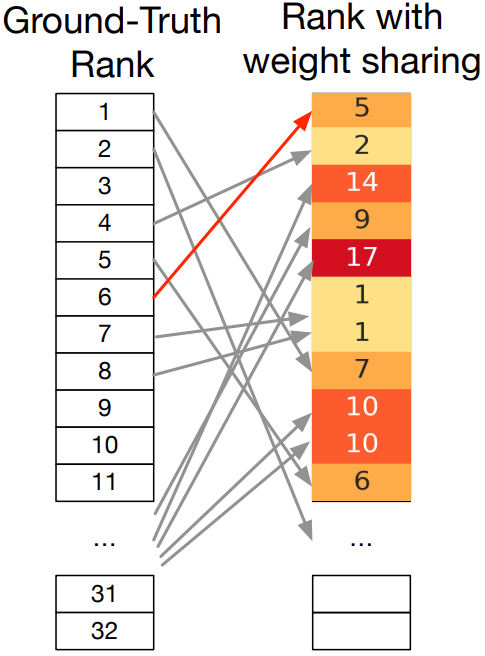
Figure 2: Illustration of rank-disorder issue from Yu et al., 2020. It occurs when the performance ordering of architectures evaluated using shared-weights (right) does not match the true architecture performance when individual weights are trained from scratch (left).
This skepticism has been reinforced by recent cases where well-known weight-sharing methods have performed poorly; in particular, DARTS was found to overfit to the upper-level validation set in a recent robustness evaluation, and both GDAS and DARTS were outperformed by standard hyperparameter optimization methods on NAS-Bench-201 given a similar time budget. Here DARTS had especially poor performance, converging to architectures consisting of only identity maps (skip-connections).
Given the questions raised about weight-sharing and recent poor results, is it time to rethink its use? In the next section we answer in the negative by showing that (a) correlation of the performance of the weight-sharing “supernet” with that of fully trained models is a sufficient but not necessary condition for weight-sharing to work, i.e. we need not be afraid of rank disorder, and (b) obtaining high-quality architectural solutions using weight-sharing mostly comes down to regularization and optimization, two well-understood aspects of machine learning.
Vanilla weight-sharing is just empirical risk minimization
Weight-sharing is made possible by the fact that architecture parameters, unlike hyperparameters such as regularization and stepsize, directly affect the loss function, in that changing from one architecture ![]() to a different architecture
to a different architecture ![]() causes a change in the loss from
causes a change in the loss from ![]() to
to ![]() , as in the latter case a different function is being used for prediction. On the other hand, changing the stepsize setting would not change the loss unless the weights were also changed by training
, as in the latter case a different function is being used for prediction. On the other hand, changing the stepsize setting would not change the loss unless the weights were also changed by training ![]() using the new stepsize; this would mean the weights were no longer shared by different hyperparameter settings.
using the new stepsize; this would mean the weights were no longer shared by different hyperparameter settings.
In fact, we can use the fact that architecture parameters can be subsumed as parameters of a supernet to pose NAS with weight-sharing as empirical risk minimization (ERM) over an extended class of functions encoded by both weights ![]() and architecture parameters
and architecture parameters ![]() :
:
![]()
Most (but not all) empirical work on NAS uses the bilevel formulation described earlier rather than solving this single-level ERM problem. However, we believe ERM should be the baseline object of study in NAS because it is better understood statistically and algorithmically; the more common bilevel optimization can be viewed as a (possibly critical) method of regularizing by splitting the data.
The single-level formulation makes clear that, rather than rank disorder, NAS can fail for either of the usual reasons ERM fails: unsuccessful optimization or poor generalization. For example, these respective failures can largely explain the issues faced by DARTS on NAS-Bench-201 and NAS-Bench-1Shot1 that were discussed above. Of course, it is not surprising that supernets might face optimization and generalization issues, since they are non-convex and over-parameterized models; however, NAS practitioners are usually very comfortable training regular deep nets, which are also non-convex and have almost as many parameters. One major difference is that, in the latter case, we have had many years of intensive effort designing regularization schemes and optimization algorithms; if we were to dedicate a similar amount of NAS research to these two issues, then perhaps we would be no more afraid of weight-sharing than we are of training standard deep nets.
One caveat to this discussion is that NAS has the additional challenge of recovering discrete architectures from continuously-relaxed architecture weights. The optimization scheme we propose next ameliorates this issue by promoting sparse architectural parameters in the first place.
Fixing differentiable NAS with weight-sharing: a geometry-aware approach
Our discussion above reduces the problem of designing NAS methods to that of designing good regularization and optimization schemes for the supernet. There has been a good amount of recent work on better regularization schemes for the supernet, including partial channel connections, penalizing the Hessian of the validation loss, and the bilevel formulation itself; we thus focus instead on improving the optimization scheme, which we do with our geometry-aware exponentiated algorithm (GAEA).
As usual, we want an optimization method that can converge to a better solution faster. In the case of weight-sharing NAS, a high-quality solution will not only have good generalization but also induce sparse architecture weights ![]() , which recall is related to the optimized parameters
, which recall is related to the optimized parameters ![]() via a softmax. We expect sparse architecture parameters to be better because, as discussed earlier, the architecture parameters are rounded in a post-processing step to derive the final discrete architecture.
via a softmax. We expect sparse architecture parameters to be better because, as discussed earlier, the architecture parameters are rounded in a post-processing step to derive the final discrete architecture.
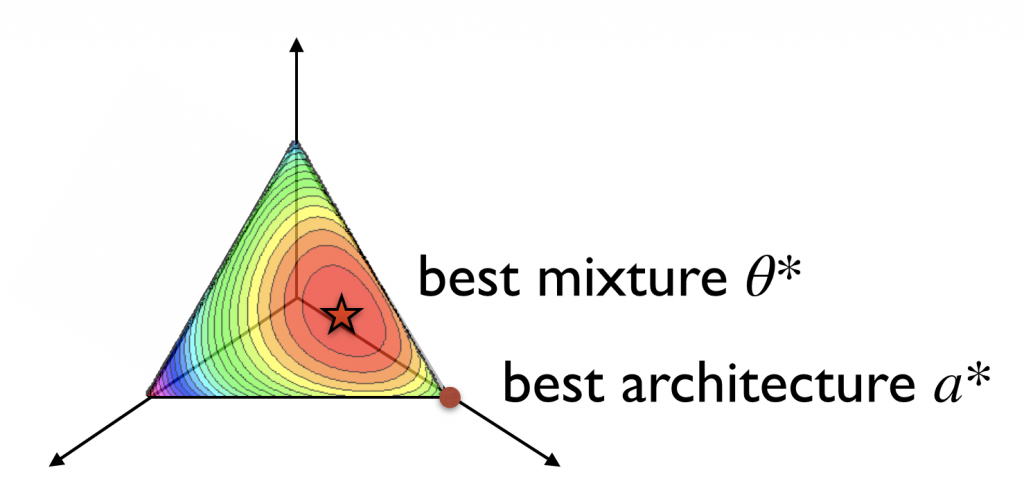
Figure 3: We want the final architecture weights ![]() to be sparse so that, when rounded, the resulting discrete architecture
to be sparse so that, when rounded, the resulting discrete architecture ![]() is close to the supernet encoded by
is close to the supernet encoded by ![]() . Otherwise the difference between the validation loss of the discrete architecture can be very different from that of the supernet. Since the elements of
. Otherwise the difference between the validation loss of the discrete architecture can be very different from that of the supernet. Since the elements of ![]() lie in a product of simplices, sparsity means that, in each simplex, a single entry is 1 and the rest are 0.
lie in a product of simplices, sparsity means that, in each simplex, a single entry is 1 and the rest are 0.
In order to achieve this, we use exponentiated gradient descent to directly optimize over the elements ![]() instead of over unconstrained values
instead of over unconstrained values ![]() . The update scheme replaces subtracting the gradient w.r.t.
. The update scheme replaces subtracting the gradient w.r.t. ![]() (line 4 in the pseudo-code) with element-wise multiplication by the negative exponentiated gradient w.r.t.
(line 4 in the pseudo-code) with element-wise multiplication by the negative exponentiated gradient w.r.t. ![]() (4.a), followed by projections to the simplices comprising
(4.a), followed by projections to the simplices comprising ![]() (4.b):
(4.b):
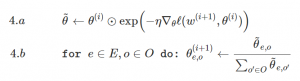
Note that each iteration is roughly as expensive as in SGD.
For convex problems, exponentiated gradient is known to be well-suited for the simplex geometry, with iteration complexity depending only logarithmically on the size ![]() of the simplex, rather than the
of the simplex, rather than the ![]() dependence of gradient descent. Under the mirror descent view of this result for linear prediction (video link), the improvement stems from the implicit regularizer encouraging larger updates when far away from a sparse target solution. For our non-convex problem, we obtain a similar guarantee by extending recent mirror descent results of Zhang & He to show that alternating the exponentiated update to the architecture parameters with SGD updates to the shared-weights yields an
dependence of gradient descent. Under the mirror descent view of this result for linear prediction (video link), the improvement stems from the implicit regularizer encouraging larger updates when far away from a sparse target solution. For our non-convex problem, we obtain a similar guarantee by extending recent mirror descent results of Zhang & He to show that alternating the exponentiated update to the architecture parameters with SGD updates to the shared-weights yields an ![]() -stationary-point in
-stationary-point in ![]() iterations. We also show experimentally in Figure 4 that this approach encourages sparser solutions than DARTS and PC-DARTS.
iterations. We also show experimentally in Figure 4 that this approach encourages sparser solutions than DARTS and PC-DARTS.
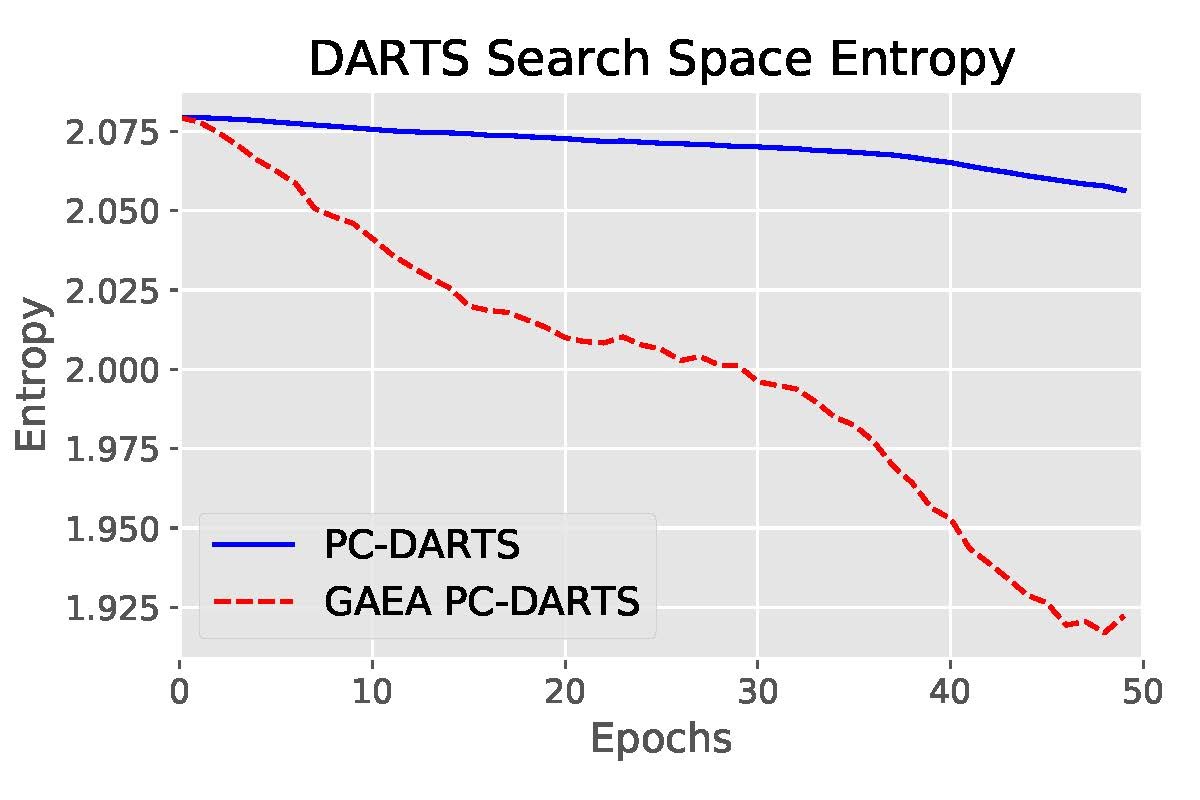
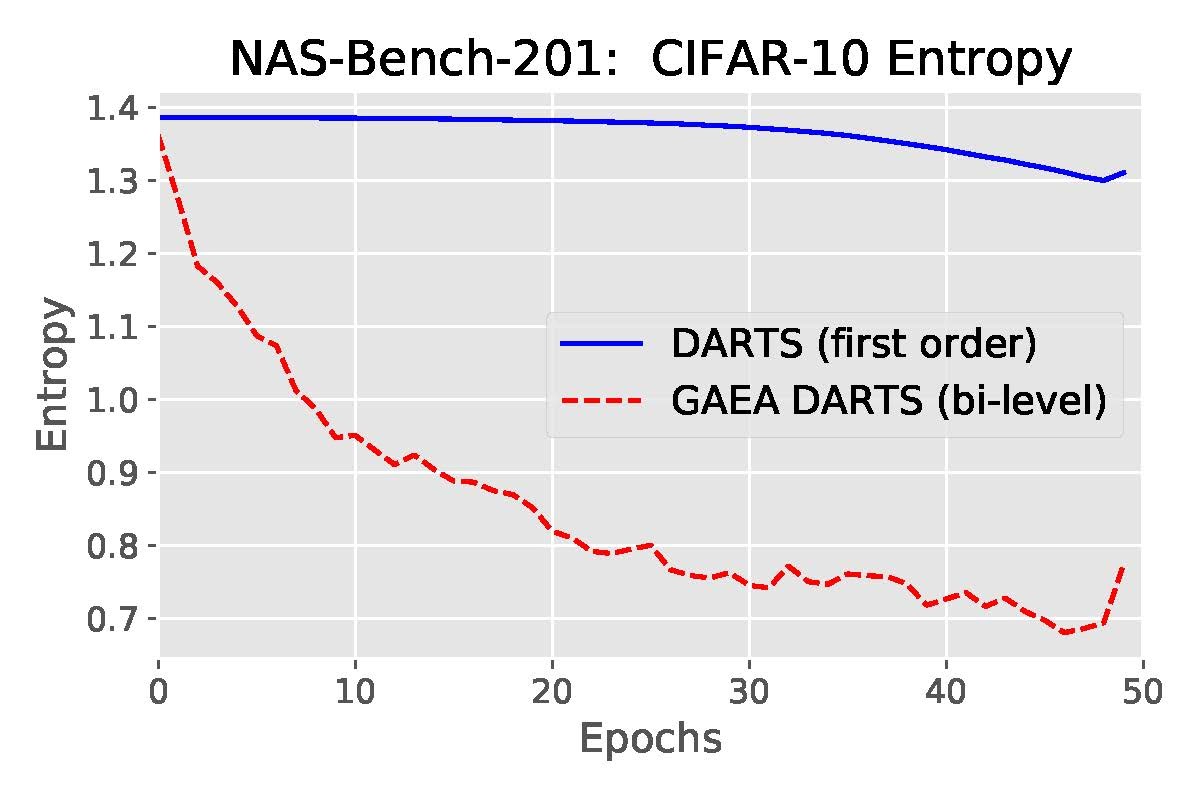
Figure 4: Sparsity of architecture weights obtained by GAEA compared to the method it modifies on two different search spaces. Sparsity is measured using average entropy across architecture decision simplices.
Our GAEA approach, which is applicable to any method using the softmax formulation described earlier (this includes DARTS, GDAS, PC-DARTS, and others), can be summarized in two simple steps:
- Replace architecture weights
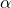 passed to the softmax with weights
passed to the softmax with weights  lying directly on the architecture decision simplices.
lying directly on the architecture decision simplices. - Use the exponentiated gradient scheme (4.a & 4.b) to update these architecture weights
 .
.
Empirical Evaluation of GAEA
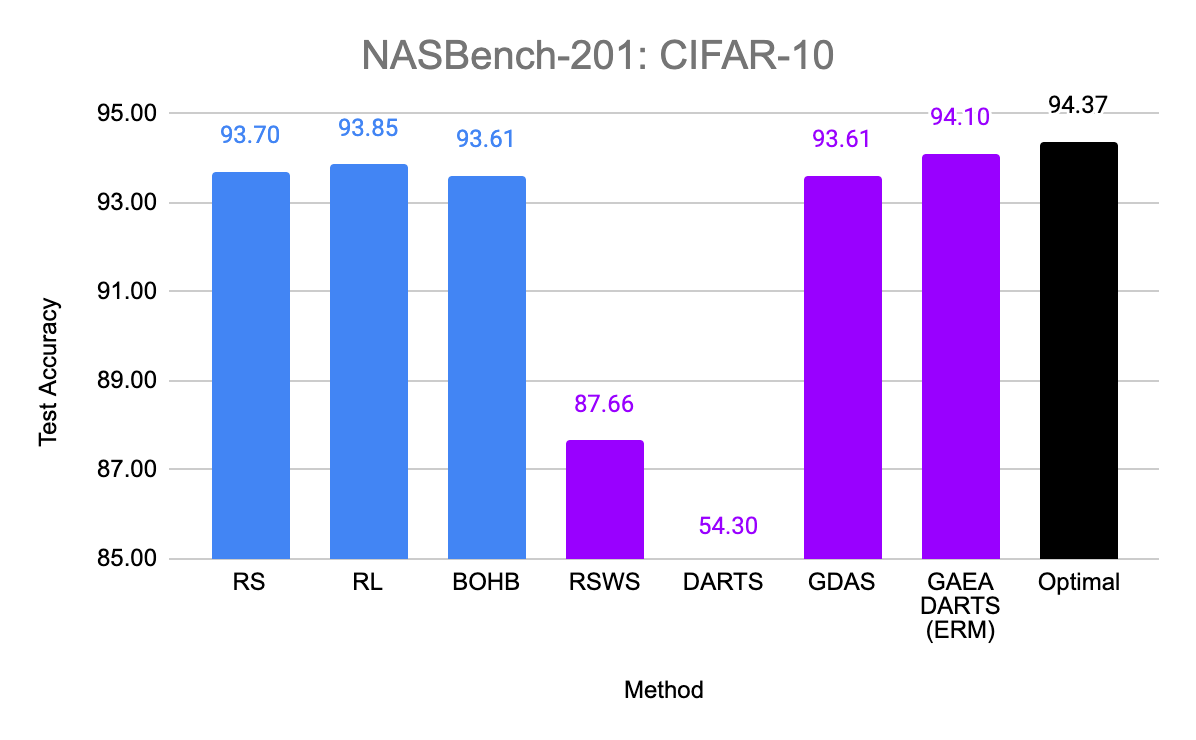
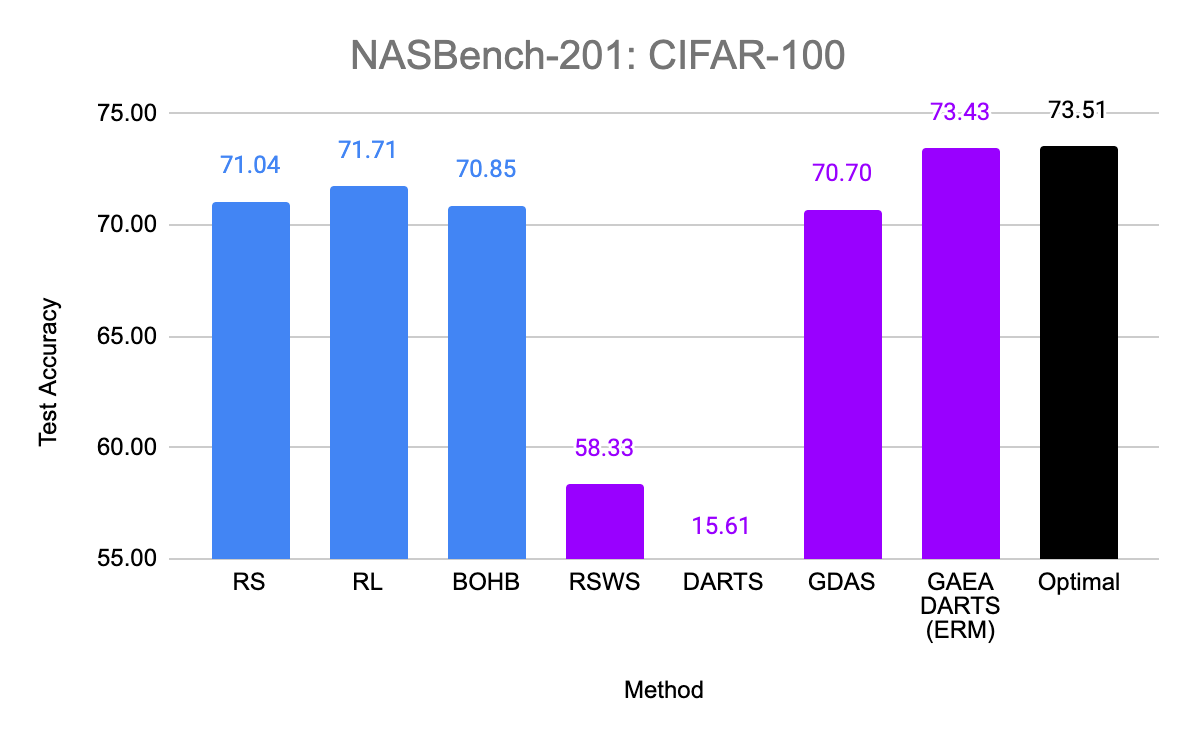

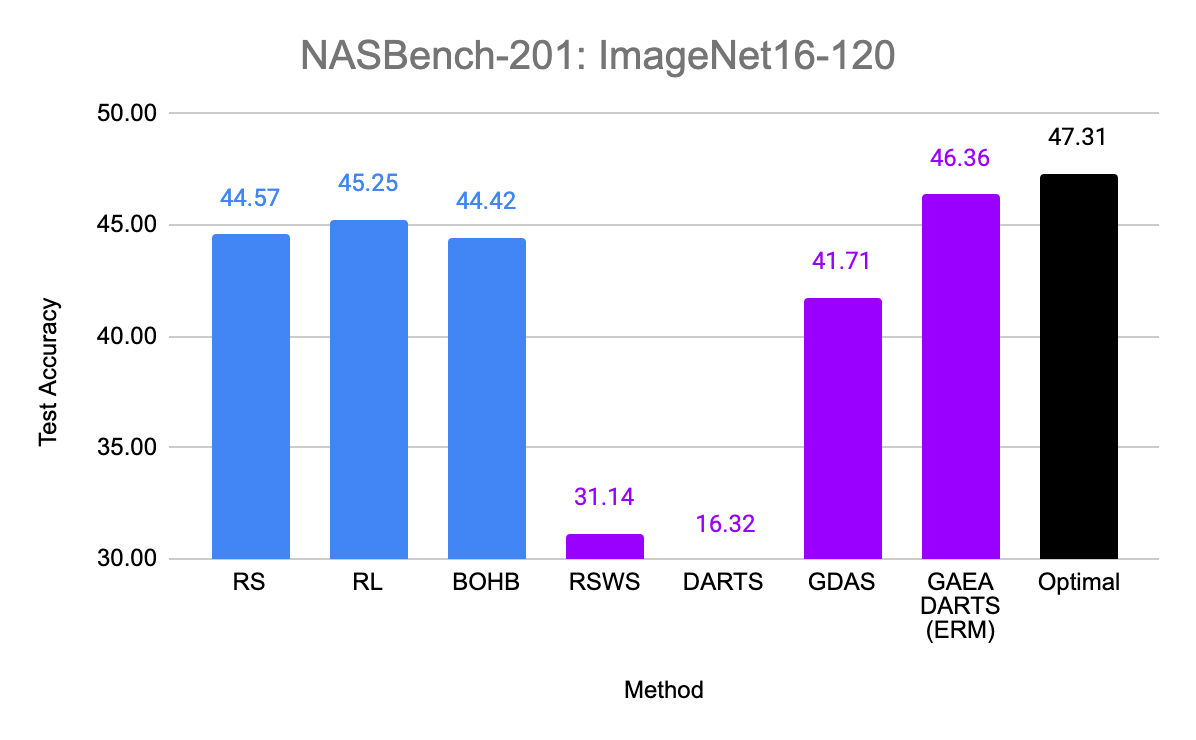
Figure 5: Evaluation of GAEA on NAS-Bench-201. Standard hyperparameter optimization methods are in blue, while weight-sharing schemes are in purple. The optimal in the search space is in black. GAEA is the first weight-sharing scheme to outperform standard hyperparameter optimization on this search space and the only one to get within a standard deviation of the optimum on two of the three datasets, CIFAR-10 and CIFAR-100.
So does the sparsity and faster convergence rates of GAEA result in better performance empirically? To test this, we simply apply the two steps above to modify existing state-of-the-art NAS methods. First, we evaluate GAEA applied to DARTS on the NAS-Bench-201 search space by Dong et al. Of the methods evaluated by Dong et al., non-weight-sharing methods outperformed weight-sharing methods on all three datasets. However, GAEA DARTS applied to the single-level ERM objective achieves the best accuracy across all three datasets, reaching near oracle-optimal performance on two of them. Notably, it fixes the catastrophically poor performance of DARTS on this space and is the only weight-sharing method that beats standard hyperparameter optimization.
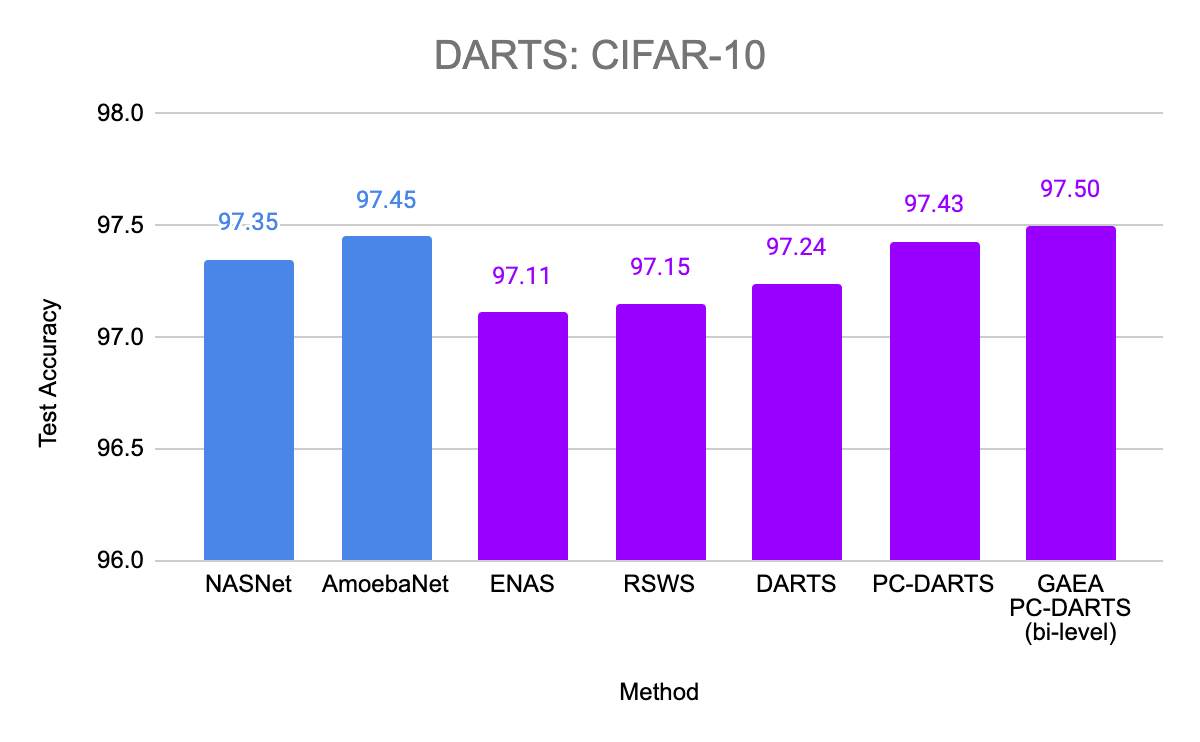
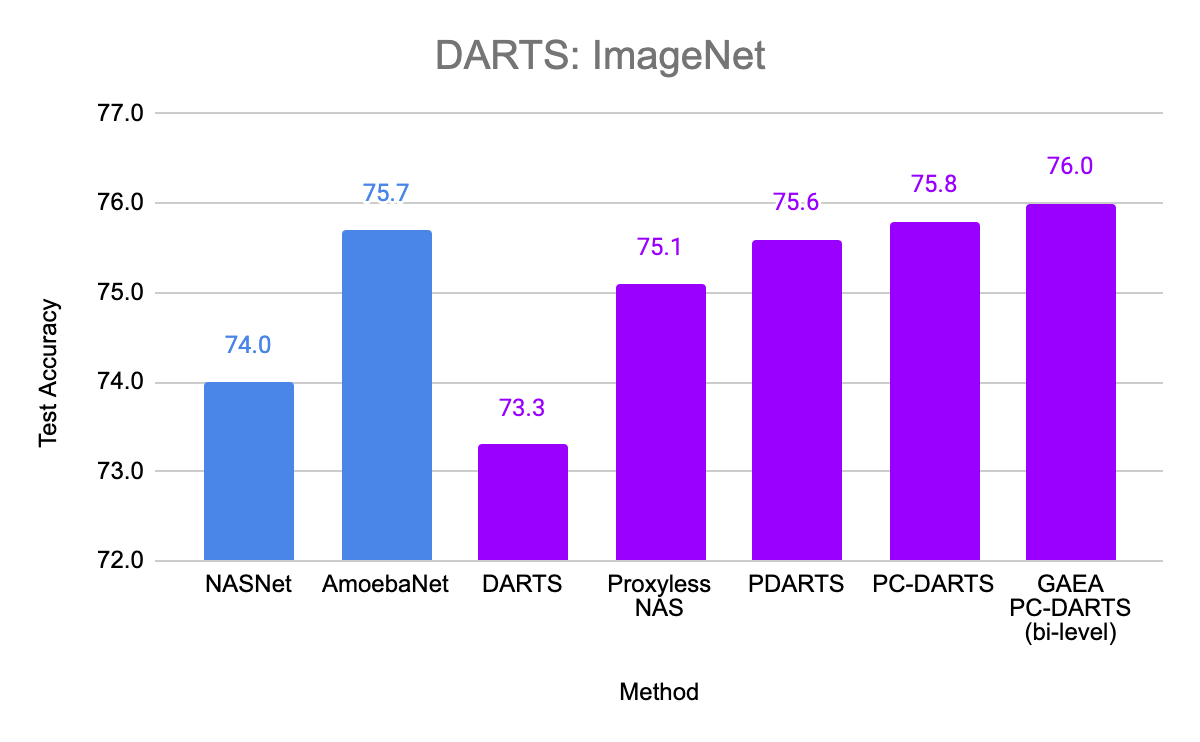
Figure 6: Evaluation of GAEA on the DARTS search space. Weight-sharing methods are in purple, while non-weight-sharing methods are in blue. Note that the non-weight-sharing methods require more than 10,000 times as many GPU-hours as GAEA for search.
We also evaluated GAEA applied to PC-DARTS on the original DARTS CNN search space. With improved regularization for the weight-sharing optimization problem, PC-DARTS was able to recently match the performance of computationally expensive non-weight-sharing methods on CIFAR-10 and ImageNet. We are able to further boost the performance of PC-DARTS with GAEA and achieve state-of-the-art performance on this search space, demonstrating the importance of efficiently optimizing in the right geometry.
Interested in learning more?
To learn more about our results, weight-sharing, and NAS you can:
- See our paper, joint with Nina Balcan and Ameet Talwalkar, for more details.
- Download our code for a full implementation of GAEA.
- Read about the original weight-sharing method, ENAS, and about the baseline weight-sharing method, RS-WS.
- Read a survey of the field (Elsken, Metzen, & Hutter, JMLR 2019).
DISCLAIMER: All opinions expressed in this posts are those of the authors and do not represent the views of CMU.
This article was initially published on the ML@CMU blog and appears here with the authors’ permission.










