☰

ΑΙhub.org

Generalizing randomized smoothing for pointwise-certified defenses to data poisoning attacks

by ML@CMU

16 October 2020

share this:

We propose a method for making black-box functions provably robust to input manipulations. By training an ensemble of classifiers on randomly flipped training labels, we can use results from randomized smoothing to certify our classifier against label-flipping attacks—the larger the margin, the larger the certified radius of robustness. Using other types of noise allows for certifying robustness to other data poisoning attacks.

Adversarial examples—targeted, human-imperceptible modifications to a test input that cause a deep network to fail catastrophically—have taken the machine learning community by storm, with a large body of literature dedicated to understanding and preventing this phenomenon (see these surveys). Understanding why deep networks consistently make these mistakes and how to fix them is one way researchers hope to make progress towards more robust artificial intelligence.

Randomized smoothing is a technique for certifying adversarial robustness whereby each prediction is accompanied by a radius in which the classifier’s prediction is guaranteed to remain constant. The technique is based on ideas from differential privacy (DP): broadly, DP ensures that a prediction does not depend too much upon any given element of the input. In a similar manner, randomized smoothing certifies that a classification cannot be too sensitive to one particular aspect of a test point—this is achieved by convolving (“smoothing”) the input with noise. This approach has recently become very popular following the first tight bound on a classifier’s radius of robustness via randomized smoothing with Gaussian noise, and it remains the only certified defense which scales to ImageNet.

In this post, we’ll describe a general strategy for repurposing randomized smoothing for a new type of certified defense to data poisoning attacks, which we call “pointwise-certified defenses”. Unlike adversarial examples, which target a classifier at test-time, a data poisoning attack is when an adversary manipulates the training data to cause undesired performance in the resulting trained model. Since modern classifiers are often trained with large amounts of data scraped from the web or directly provided by users (e.g. recommendation engines), robustness to manipulations of such data is crucial for trusting the output of our models.

The pointwise-certified defenses we introduce differ from existing defenses in that they guarantee that the classifier’s prediction will not change if an adversary manipulates the training data, rather than guaranteeing that the prediction is correct. This type of certificate is preferable when we are making a sensitive decision, such as granting a loan or parole, and we want to ensure that no one could have messed with the training data to force a particular outcome. This approach also has connections to fairness in AI: as an example, by certifying robustness to modifications of a particular feature, we can guarantee that our classifier is not relying too heavily on that feature to make its prediction.

We’ll also demonstrate a specific implementation of our proposed modification which results in the first pointwise-certified defense to label-flipping attacks. We begin with a (very) brief overview of randomized smoothing. For a more detailed description, see our paper from ICML ’19 or this excellent talk by Zico Kolter (timestamped to start at the relevant section).

Randomized Smoothing for Certified Adversarial Robustness

Given a trained (“base”) classifier $f$ and an input $x$ , the objective of adversarial robustness is to ensure that an adversary cannot change the classification of $x$ with an imperceptibly small perturbation of $x$ . For randomized smoothing, instead of directly certifying $f$ , we define a new, “smoothed” classifier $g$ whose prediction is the majority vote of $f$ applied to $x$ convolved with some noise distribution $p$ . Formally, for a set of classes $\mathcal{C}$ ,

(1) $g(x) = \arg\max_{c\in\mathcal{C}}\mathbb{E}_{\epsilon\sim p(\epsilon)}[f(x+\epsilon)_c],$

where $f$ outputs a distribution over classes and the subscript indicates indexing. Unlike $f$ , this new classifier $g$ will have provably smooth decision boundaries. As a result, we are able to guarantee that the output of $g$ will not change within a certain radius $R$ of the input $x$ , where the magnitude of this radius is a function of the margin by which the majority vote wins: the larger the margin, the larger the certified radius. For example, when classifying images, $R$ could be the $\ell_2$ -norm of a pixel perturbation. The image below shows an example of $f$ , the noise distribution, and the resulting $g$ .

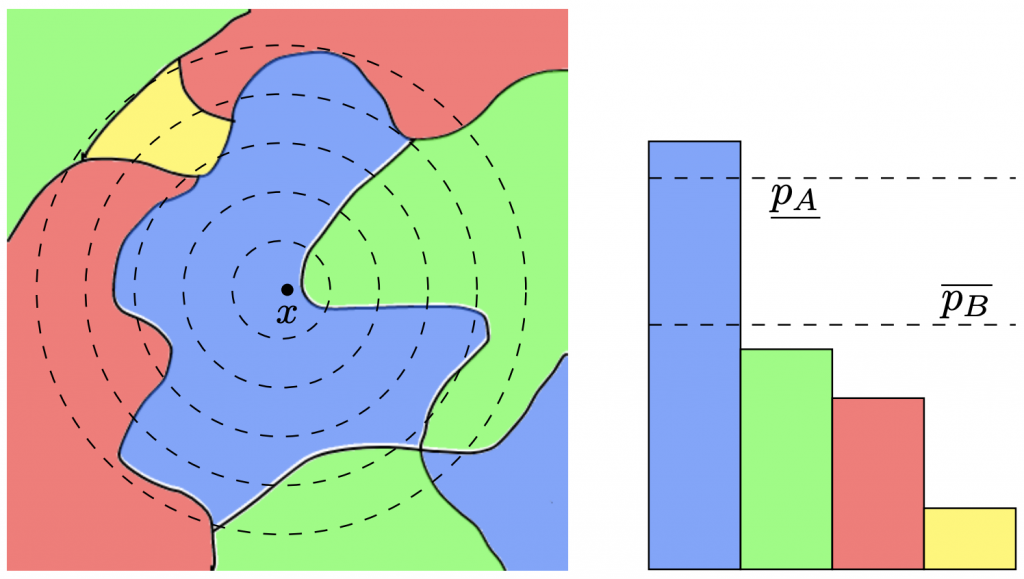
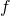We plot the base classifier $f$ and its integrated decision regions 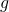$g$ —both predict “blue” for 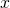$x$ . **Left**: The decision regions of the base classifier 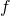$f$ , where each color signifies a different class. The dotted lines are the level sets of the Gaussian noise distribution centered at 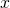$x$ . Observe that a small perturbation of 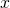$x$ could cause 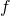$f$ to predict “green”. Right: The decision regions, integrated with respect to the noise. 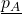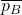$\underline{p_A}$ and $\overline{p_B}$ are high-probability lower and upper bounds on “blue” and “green”, respectively. A small perturbation could shrink the gap, but we can guarantee that it will not change which class wins the majority. That is, 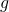$g$ ’s prediction will not change.

To determine the margin, we need to calculate (1) above. In practice, we cannot integrate the complex decision regions of a neural network, so the expectation cannot be exactly evaluated. Instead, it is typically approximated via Monte Carlo sampling—by creating many noisy versions of the image and classifying them, we can sample from the expected distribution over classes, which gives us an estimate of the actual probabilities. This means that the certificate of robustness is only true with high probability: by taking more samples, we can increase this probability, but we would need infinite samples to reach a certificate that is 100% guaranteed. Another key point here is that we are unable to guarantee that the output of the smoothed classifier is correct; we are instead guaranteeing that its output will not change for any input within the certified radius.

Generalizing Randomized Smoothing to Arbitrary Functions

All previous applications of randomized smoothing involve injecting noise into the input of a classifier at test-time, resulting in certified robustness to adversarial attacks (typically $\ell_p$ -norm pixel perturbations). However, in our recent ICML publication, we observe that the theory behind randomized smoothing applies to arbitrary functions, not just classifiers. That is, convolving a function’s input with the right noise allows us to certify robustness of that function to any type of input corruption—using pixel noise to defend against pixel perturbations is just one particular application! By defining an appropriate noise distribution, we can leverage advances in randomized smoothing (e.g., Lee et al. 2019, Dvijotham et al. 2020) to certify robustness of black-box functions to arbitrary input perturbations.

In particular, we consider the base function $f$ to include the entire training procedure of the classifier, meaning it takes as input the training set in addition to the test input to be classified. Analogous to injecting pixel noise at test time, we can derive robustness guarantees by injecting noise into the training set at train time—this will allow us to certify robustness to adversarial modifications of the training set (i.e., data poisoning attacks).

**Top**: Existing applications of randomized smoothing inject pixel noise at test time to certify robustness to adversarial pixel pertubations. **Bottom**: Our proposed generalization of randomized smoothing. Injection of different types of noise allows us to certify robustness of arbitrary black-box functions. Here, we give the example of certifying robustness to label-flipping attacks.

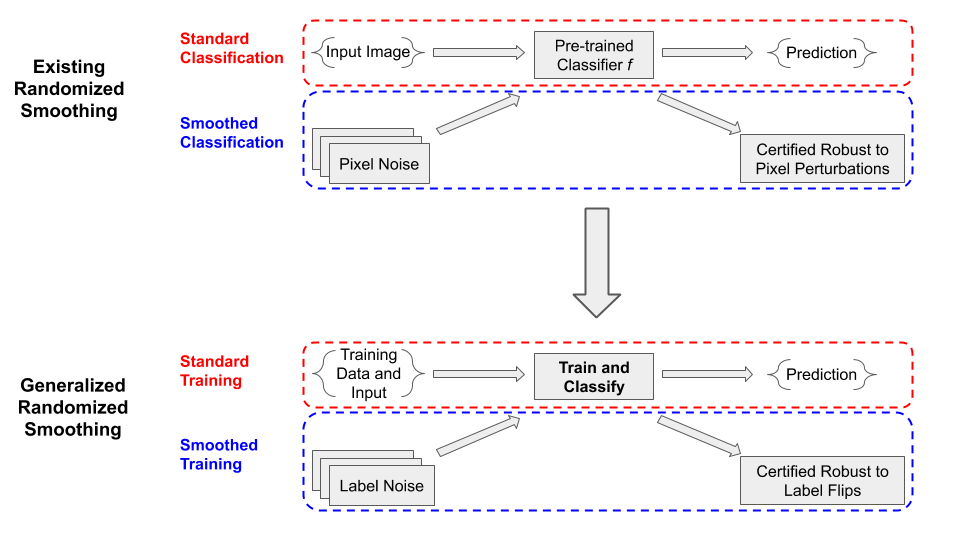
Here we recall the distinction between guaranteeing correctness of the classifier and guaranteeing constancy. In the context of data poisoning attacks, the robustness guaranteed by randomized smoothing is different from the usual meaning of “certified defense”.

Existing works on certified defenses or robust regression (Steinhardt et al. 2017, Prasad et al. 2018) guarantee their performance on the test distribution as a whole, but have no way of determining if a particular input will be misclassified. If an adversary specifically wants to cause one particular point to be misclassified (as in a backdoor attack), these defenses make no guarantees. In contrast, the defense we’ve derived via randomized smoothing is what we refer to as a “pointwise-certified defense”. While we cannot guarantee accuracy on the test set, what we can guarantee is that our classifier’s output could not have been changed by an adversary’s modification of the training set—if it’s wrong, it would have been wrong anyways. As we noted in the introduction, this type of certificate is preferable for making important, sensitive decisions rather than large-scale classifications over a broad test set.

Implementing the Strategy for Pointwise-Certified Robustness to Label-Flipping Attacks

Ok, so we’ve demonstrated how to generalize randomized smoothing to provide pointwise-certified robustness guarantees. As a specific demonstration of this framework, we now show how to implement our strategy to provide a classification algorithm that is robust to label-flipping attacks. As described above, this can be done by injecting label noise at test time and invoking existing randomized smoothing bounds. Is it really just that simple?

Not quite! We still need to somehow evaluate the integral—in traditional randomized smoothing, this is done by repeatedly sampling noise $\epsilon\sim p(\epsilon)$ and then re-evaluating the classifier $f(x+\epsilon).$ So why can’t we do the exact same thing here? Remember that the base function $f$ now includes the entire training procedure; this would entail training a new classifier, from scratch, for each sample. Since we need thousands of samples for a meaningful bound, this is wildly intractable.

Instead, we make the following simplification: instead of training classifiers from scratch, we assume the existence of a pre-trained feature embedder and then we learn to separate the data in feature space via least-squares classification. To get an appropriate feature embedder, we can rely on the power of transfer learning. Alternatively, since a label-flipping attack cannot modify the inputs themselves, we can leverage advancements in deep unsupervised and self-supervised learning to learn meaningful features without relying on the potentially poisoned labels.

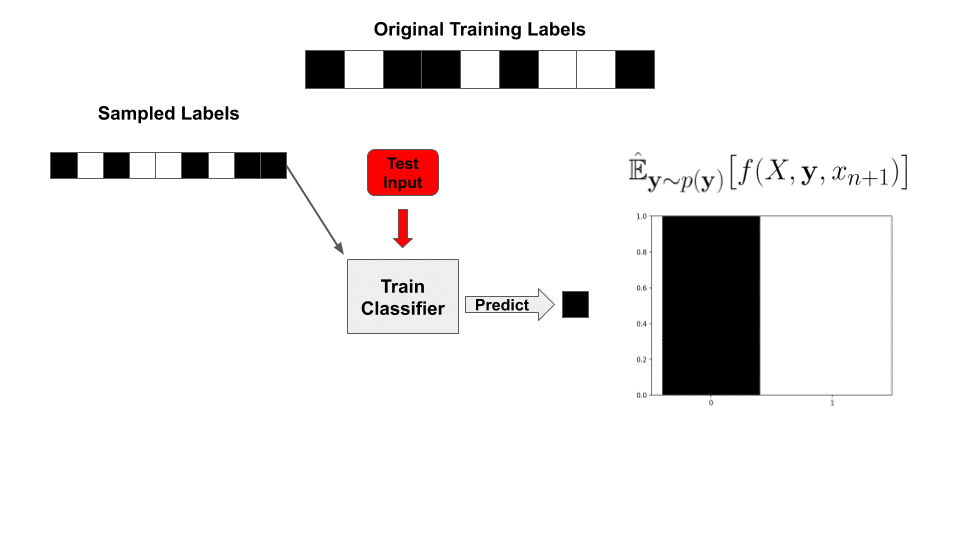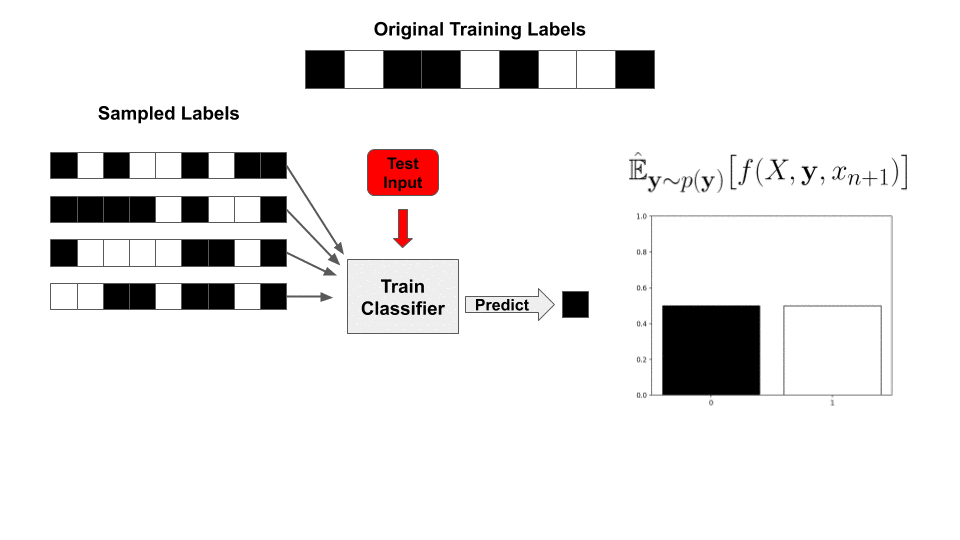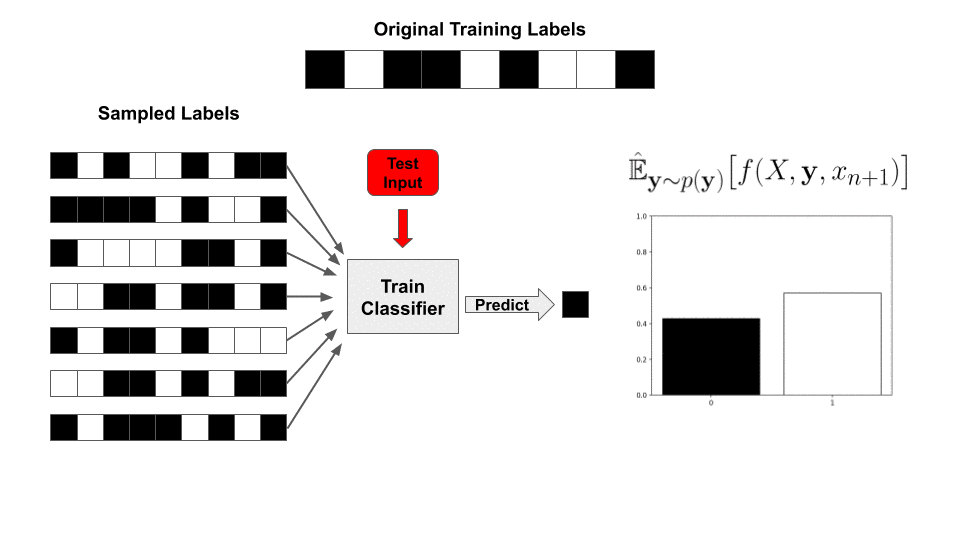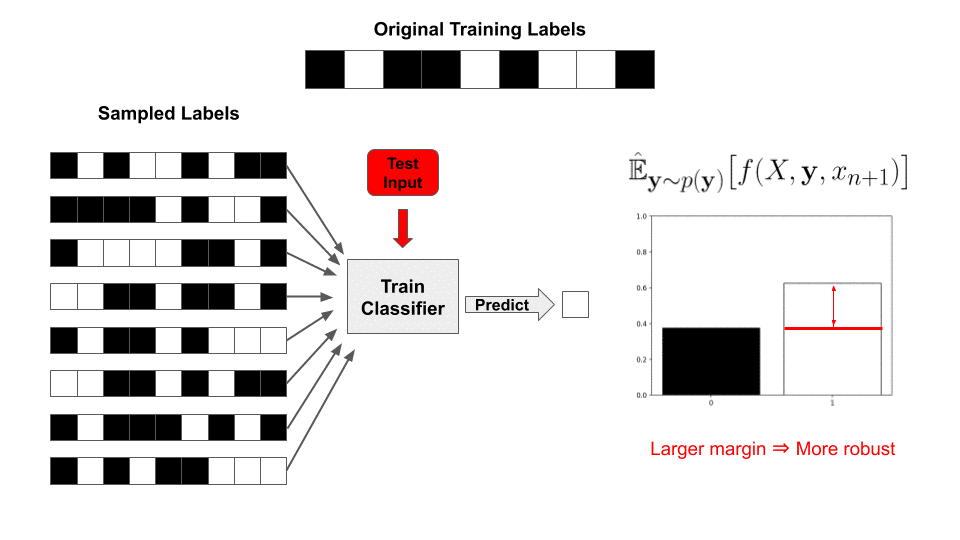
Why does least-squares classification make sampling tractable? Given training data $X\in\mathbb{R}^{n\times k}$ (already in feature space), binary labels $\mathbf{y}\in\{0,1\}^n$ , and a test point $x_{n+1}\in\mathbb{R}^k$ , we can write our prediction as

$\hat\beta = (X^\top X)^{-1} X^\top \mathbf{y},$

$\hat y_{n+1} = \mathbf{1}\{\hat\beta^\top x_{n+1} \geq 1/2\}.$

Equivalently, for a fixed test point, we can define the following “kernel” vector:

$\boldsymbol{\alpha} = X(X^\top X)^{-1} x_{n+1}^\top.$

With this value precomputed, for a newly sampled set of labels $\mathbf{y'}$ , our classifier’s prediction is reduced to a simple inner product with the labels!

$\hat y_{n+1} = \mathbf{1}\{\boldsymbol\alpha^\top \mathbf{y'} \geq 1/2\}.$

This means the entire “train and classify” procedure has been reduced to a matrix-vector product and a set of embarrassingly parallel $\mathcal{O}(n)$ operations. Specifically, we pre-calculate $\boldsymbol\alpha$ and then approximate the expectation by sampling labels $\mathbf{y'}$ and evaluating the classifier for each sample:

$\mathbb{E}_{\mathbf{y'}\sim p(\mathbf{y})}[\mathbf{1}\{\boldsymbol\alpha^\top \mathbf{y'} \geq 1/2\}].$

Eliminating Sampling Altogether

With a little more work, we can actually completely eliminate the need for repeated sampling. This simultaneously reduces the computational complexity of certification and makes such certifications deterministic, unlike traditional “with high probability” randomized smoothing certificates.

To make this work, observe that we are using the samples to evaluate a lower bound on the integral:

$\mathbb{E}_{\mathbf{y'}\sim p(\mathbf{y})}[\mathbf{1}\{\boldsymbol\alpha^\top \mathbf{y'} \geq 1/2\}] = P(\boldsymbol\alpha^\top \mathbf{y'} \geq 1/2).$

Equivalently, we want an upper bound on $P(\boldsymbol\alpha^\top \mathbf{y'} \leq 1/2)$ . If the label noise is dimension-wise independent, the inner product $\boldsymbol\alpha^\top \mathbf{y'}$ is the sum of $n$ independent random variables. This means we can derive a sharp concentration inequality via the Chernoff bound:

$P(\boldsymbol\alpha^\top \mathbf{y'} \leq 1/2) \leq \min_{t>0}\left\{e^{t/2}\prod_{i=1}^n \mathbb{E}[e^{-t\alpha_i\mathbf{y'}_i}]\right\}.$

This is a one-dimensional optimization problem which is log-convex in $t$ , so we can easily calculate a sharp lower bound on this integral with Newton’s method! Even better, the bound is no longer probabilistic. By evaluating this analytical expression, we’ve derived the first truly guaranteed randomized smoothing certificate. Note that in the event that this upper bound is greater than $1/2$ , we can instead bound the opposite event. Further, we can straightforwardly extend our defense to the multi-class case (we won’t go into the details here, but it’s covered in Appendix B in the paper).

Experiments

We’d like to get a sense of how well our certified classifier defends against an adversary compared to an undefended neural network. In the certified adversarial robustness literature, a common metric to measure this is the certified test set accuracy. This is a function of the strength of an adversary: given an adversary with a particular “perturbation budget”, certified accuracy is the percentage of the test set that is both correctly classified and certified to not change under attack. Note that this function is always monotonically decreasing.

Above is the certified accuracy of our classifier on MNIST 1/7 (MNIST restricted to just the digits 1 and 7). In our case, the perturbation budget allotted to an adversary is a specific number of label flips during training—this is also expressed as a percentage of the total training set on the top x-axis. For context, the plot includes the empirical test set accuracy of a standard, undefended neural network. Our classifier vastly outperforms this baseline; the undefended classifier does worse than random once only 4% of the training labels have been flipped, while our classifier certifiably maintains 75% accuracy. The hyperparameter $q$ can be interpreted as a proxy for the variance of the noise distribution from which we sample the labels. Just like in previous randomized smoothing applications, we see that $q$ controls a trade-off between accuracy and robustness. Higher $q$ results in lower “uncertified” accuracy where the number of label flips $N=0$ , but the classifier’s certified accuracy decays more slowly as $N$ grows.

Conclusion

This work introduces a method of repurposing randomized smoothing for “pointwise-certified robustness” of arbitrary black-box functions. As a first step and proof-of-concept, we develop an algorithm for robustness to label-flipping attacks, but there are many other possible directions where this strategy could be taken: some follow-up work already builds upon our idea to robustify classifiers to backdoor attacks and general data poisoning attacks. More broadly, our framework allows for pointwise certification to any type of input modification, recalling the differential privacy origins of randomized smoothing.

For more details, experimental results, and discussion, check out the paper:

Certified Robustness to Label-Flipping Attacks via Randomized Smoothing
Elan Rosenfeld, Ezra Winston, Pradeep Ravikumar, J. Zico Kolter
International Conference on Machine Learning 2020

Acknowledgements: Thanks to Mariya Toneva, Misha Khodak, and Ben Eysenbach for feedback on this post.

DISCLAIMER: All opinions expressed in this post are those of the author and do not represent the views of CMU.

This article was initially published on the ML@CMU blog and appears here with the authors’ permission.

ML@CMU

AIhub is supported by:

Generalizing randomized smoothing for pointwise-certified defenses to data poisoning attacks

Related posts :

Are emergent abilities of large language models a mirage? – Interview with Brando Miranda

We built an AI tool to help set priorities for conservation in Madagascar: what we found

Interview with Mike Lee: Communicating AI decision-making through demonstrations

Machine learning viability modelling of vertical-axis wind turbines

The Machine Ethics podcast: What is AI? Volume 3

DataLike: Interview with Tẹjúmádé Àfọ̀njá

↑