
ΑΙhub.org
On learning language-invariant representations for universal machine translation
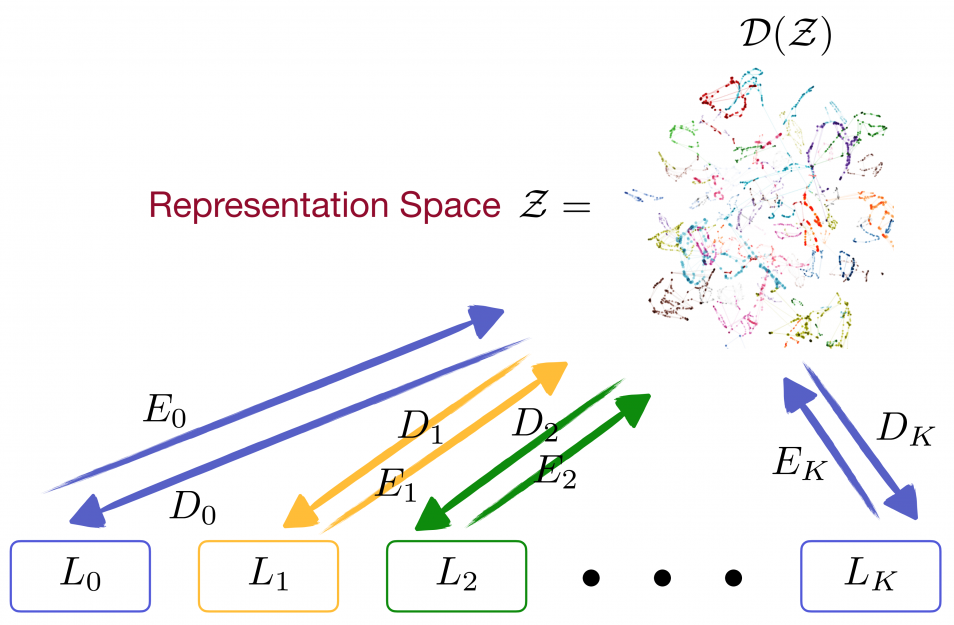
 over the representation space
over the representation space  , from which sentences of language
, from which sentences of language  are generated via decoder
are generated via decoder 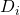 . Similarly, sentences could also be encoded via
. Similarly, sentences could also be encoded via 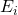 to
to 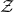 .
.By Han Zhao and Andrej Risteski
Despite the recent improvements in neural machine translation (NMT), training a large NMT model with hundreds of millions of parameters usually requires a collection of parallel corpora at a large scale, on the order of millions or even billions of aligned sentences for supervised training (Arivazhagan et al.). While it might be possible to automatically crawl the web to collect parallel sentences for high-resource language pairs, such as German-English and French-English, it is often infeasible or expensive to manually translate large amounts of sentences for low-resource language pairs, such as Nepali-English, Sinhala-English, etc. To this end, the goal of the so-called multilingual universal machine translation, a.k.a., universal machine translation (UMT), is to learn to translate between any pair of languages using a single system, given pairs of translated documents for some of these languages. The hope is that by learning a shared “semantic space” between multiple source and target languages, the model can leverage language-invariant structure from high-resource translation pairs to transfer to the translation between low-resource language pairs, or even enable zero-shot translation.
Indeed, training such a single massively multilingual model has gained impressive empirical results, especially in the case of low-resource language pairs (see Fig. 2). However, such success also comes with a cost. From Fig. 2 we observe that the translation quality over high-resource language pairs by using such a single UMT system is worse than the corresponding bilingual baselines.

Is this empirical phenomenon by coincidence? If not, why does it happen? Furthermore, what kind of structural assumptions about languages could help us get over this detrimental effect? In this blog post, based on our recent ICML paper, we take the first step towards understanding universal machine translation by providing answers to the above questions. The key takeaways of this blog post could be summarized as follows:
- In a completely assumption-free setup, based on a common shared representation, no matter what decoder is used to translate the target languages, it is impossible to avoid making a large translation error on at least one pair of the translation pairs.
- Under a natural generative model assumption for the data, after seeing aligned sentences for a linear number of language pairs (instead of quadratic!), we can learn encoder/decoders that perform well on any unseen language pair, i.e., zero-shot translation is possible.
An Impossibility Theorem on UMT via Language-Invariant Representations
Suppose we have an unlimited amount of parallel sentences for each pair of languages, with unbounded computational resources. Could we train a single model that performs well on all pairs of translation tasks based on a common representation space? Put it in other words, is there any information-theoretic limit of such systems for the task of UMT? In this paragraph we will show that there is an inherent tradeoff between the translation quality and the degree of representation invariance w.r.t. languages: the better the language invariance, the higher the cost on at least one of the translation pairs. At a high-level, this result holds due to the general data-processing principle: if a representation is invariant to multiple source languages, then any decoder based on this representation will have to generate the same language model on the target language. But on the other hand, the parallel corpora we use to train such a system could have drastically different sentence distributions on the target language, thus leading to a discrepancy (error) between the generated sentence distribution and the ground-truth sentence distribution over the target language.
To keep our discussions simple and transparent, let’s start with a basic Two-to-One setup where there are only two source languages ![]() and
and ![]() and one target language
and one target language ![]() . Furthermore, for each source language
. Furthermore, for each source language ![]() , let’s assume that there is a perfect translator
, let’s assume that there is a perfect translator ![]() that takes a sentence (or string, sequence) from
that takes a sentence (or string, sequence) from ![]() and outputs the corresponding translation in
and outputs the corresponding translation in ![]() . Under this setup, it is easy to see that there exists a perfect translator
. Under this setup, it is easy to see that there exists a perfect translator ![]() in this Two-to-One task:
in this Two-to-One task:
![]()
In words: upon receiving a sentence ![]() ,
, ![]() simply checks which source language
simply checks which source language ![]() comes from and then call the corresponding ground-truth translator.
comes from and then call the corresponding ground-truth translator.
To make the idea of language-invariant representations formal, let ![]() be an encoder that takes a sentence (string) from alphabet
be an encoder that takes a sentence (string) from alphabet ![]() to a representation in a vector space
to a representation in a vector space ![]() . We call
. We call ![]() an
an ![]() –universal language mapping if the distributions of sentence representations from different languages
–universal language mapping if the distributions of sentence representations from different languages ![]() and
and ![]() are
are ![]() -close to each other. In words,
-close to each other. In words, ![]() for some divergence measure
for some divergence measure ![]() , where
, where ![]() is the induced distribution of sentence (from
is the induced distribution of sentence (from ![]() ) representations in the shared space
) representations in the shared space ![]() . Subsequently, a multilingual system will train a decoder
. Subsequently, a multilingual system will train a decoder ![]() that takes a sentence representation
that takes a sentence representation ![]() and outputs the corresponding target translation in language
and outputs the corresponding target translation in language ![]() . The hope here is that
. The hope here is that ![]() encodes the language-invariant semantic information about the input sentence (either from
encodes the language-invariant semantic information about the input sentence (either from ![]() or from
or from ![]() ) based on which to translate to the target language
) based on which to translate to the target language ![]() .
.
So far so good, but could we recover the perfect translator ![]() by learning a common, shared representation
by learning a common, shared representation ![]() , i.e.,
, i.e., ![]() is small? Unfortunately, the answer here is negative if we don’t have any assumption on the parallel corpora we use to train our encoder
is small? Unfortunately, the answer here is negative if we don’t have any assumption on the parallel corpora we use to train our encoder ![]() and decoder
and decoder ![]() :
:
Theorem (informal): Let
be an
-universal language mapping. Then for any decoder
, the following lower bound holds:
Here the error term ![]() measures the
measures the ![]() translation performance given by the encoder-decoder pair
translation performance given by the encoder-decoder pair ![]() from
from ![]() to
to ![]() over distribution
over distribution ![]() . The first term
. The first term ![]() in the lower bound measures the difference of distributions over sentences from the target language in the two parallel corpora, i.e.,
in the lower bound measures the difference of distributions over sentences from the target language in the two parallel corpora, i.e., ![]() and
and ![]() . For example, in many practical scenarios, it may happen that the parallel corpus of high-resource language pair, e.g., German-English, contains sentences over a diverse domain whereas as a comparison, the parallel corpus of low-resource language pair, e.g., Sinhala-English, only contains target translations from a specific domain, e.g., sports, news, product reviews, etc. In this case, despite the fact that the target is the same language
. For example, in many practical scenarios, it may happen that the parallel corpus of high-resource language pair, e.g., German-English, contains sentences over a diverse domain whereas as a comparison, the parallel corpus of low-resource language pair, e.g., Sinhala-English, only contains target translations from a specific domain, e.g., sports, news, product reviews, etc. In this case, despite the fact that the target is the same language ![]() , the corresponding sentence distributions from English are quite different between different corpora, leading to a large lower bound. As a result, our theorem, which could be interpreted as a kind of uncertainty principle in UMT, says that no matter what kind of decoder we are going to use, it has to incur a large error on at least one of the translation pairs. It is also worth pointing out that our lower bound is algorithm-independent and it holds even with unbounded computation and data. As a final note, realize that for fixed distributions
, the corresponding sentence distributions from English are quite different between different corpora, leading to a large lower bound. As a result, our theorem, which could be interpreted as a kind of uncertainty principle in UMT, says that no matter what kind of decoder we are going to use, it has to incur a large error on at least one of the translation pairs. It is also worth pointing out that our lower bound is algorithm-independent and it holds even with unbounded computation and data. As a final note, realize that for fixed distributions ![]() , the smaller the
, the smaller the ![]() (hence the better the language-invariant representations), the larger the lower bound, demonstrating an inherent tradeoff between language-invariance and translation performance in general.
(hence the better the language-invariant representations), the larger the lower bound, demonstrating an inherent tradeoff between language-invariance and translation performance in general.
Proof Sketch: Here we provide a proof-by-picture (Fig. 3) in the special case of perfectly language-invariant representations, i.e., ![]() , to highlight the main idea in our proof of the above impossibility theorem. Please refer to our paper for more detailed proof as well as an extension of the above impossibility theorem in the more general many-to-many translation setting.
, to highlight the main idea in our proof of the above impossibility theorem. Please refer to our paper for more detailed proof as well as an extension of the above impossibility theorem in the more general many-to-many translation setting.
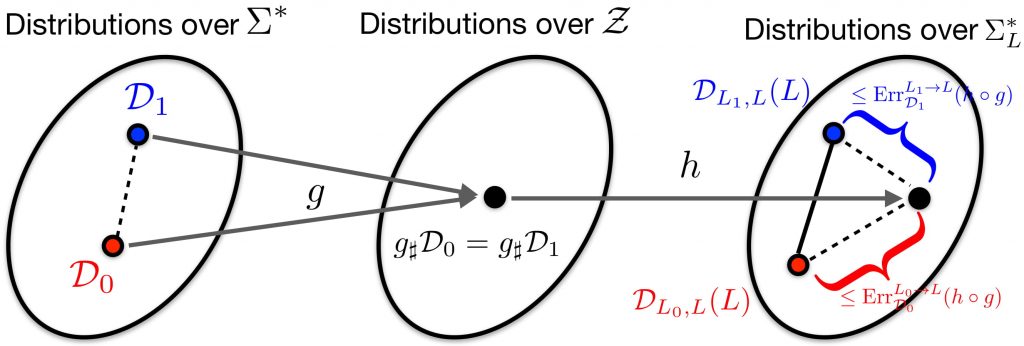
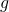 induces the same feature distribution over
induces the same feature distribution over 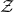 , which leads to the same output distribution over the target language
, which leads to the same output distribution over the target language 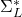 . However, the parallel corpora of the two translation tasks in general have different marginal distributions over the target language, hence a triangle inequality over the output distributions gives the desired lower bound.
. However, the parallel corpora of the two translation tasks in general have different marginal distributions over the target language, hence a triangle inequality over the output distributions gives the desired lower bound.How can we Bypass this Limitation?
One way is to allow the decoder ![]() to have access to the input sentences (besides the language-invariant representations) during the decoding process — e.g. via an attention mechanism on the input level. Technically, such information flow from input sentences during decoding would break the Markov structure of “input-representation-output” in Fig. 3, which is an essential ingredient in the proof of our theorem. Intuitively, in this case both language-invariant (hence language-independent) and language-dependent information would be used.
to have access to the input sentences (besides the language-invariant representations) during the decoding process — e.g. via an attention mechanism on the input level. Technically, such information flow from input sentences during decoding would break the Markov structure of “input-representation-output” in Fig. 3, which is an essential ingredient in the proof of our theorem. Intuitively, in this case both language-invariant (hence language-independent) and language-dependent information would be used.
Another way would be to assume extra structure on the distributions of our corpora ![]() , i.e., by assuming some natural generative process capturing the distribution of the parallel corpora that are used for training. Since languages share a lot of semantic and syntactic characteristics, this would make a lot of sense — and intuitively, this is what universal translation approaches are banking on. In the next paragraph, we will do exactly this — we will show that under a suitable generative model, not only will there be a language-invariant representation, but it will be learnable using corpora from a very small (linear) number of pairs of language.
, i.e., by assuming some natural generative process capturing the distribution of the parallel corpora that are used for training. Since languages share a lot of semantic and syntactic characteristics, this would make a lot of sense — and intuitively, this is what universal translation approaches are banking on. In the next paragraph, we will do exactly this — we will show that under a suitable generative model, not only will there be a language-invariant representation, but it will be learnable using corpora from a very small (linear) number of pairs of language.
A Generative Model for UMT: A Linear Number of Translation Pairs Suffices!
In this section we will discuss a generative model, under which not only will there be a language-invariant representation, but it will be learnable using corpora from a very small (linear) number of pairs of language. Note that there are a quadratic number of translation pairs in our universe, hence our result shows that under this generative model zero-shot translation is actually possible.
To start with, what kind of generative model is suitable for the task of UMT? Ideally, we would like to have a feature space where vectors correspond to the semantic encoding of sentences from different languages. One could also understand it as a sort of “meaning” space. Then, language-dependent decoders would take these semantic vectors and decode them as the observable sentences. Figure 1 illustrates the generative process of our model, where we assume there is a common distribution ![]() over the feature space
over the feature space ![]() , from which parallel sentences are sampled and generated.
, from which parallel sentences are sampled and generated.
For ease of presentation, let’s first assume that each encoder-decoder pair ![]() consists of deterministic mappings (see our paper on extensions with randomized encoders/decoders). The first question to ask is: how does this generative model assumption circumvent our previous lower bound in the last paragraph? We can easily observe that under the encoder-decoder generative assumption in Figure 1, the first term in our lower bound,
consists of deterministic mappings (see our paper on extensions with randomized encoders/decoders). The first question to ask is: how does this generative model assumption circumvent our previous lower bound in the last paragraph? We can easily observe that under the encoder-decoder generative assumption in Figure 1, the first term in our lower bound, ![]() , gracefully reduces to 0, hence even if we try to learn perfectly language-invariant representations (
, gracefully reduces to 0, hence even if we try to learn perfectly language-invariant representations (![]() ), there will be no loss of translation accuracy using universal language mapping. Perhaps what’s more interesting is that, under proper assumptions on the structure of
), there will be no loss of translation accuracy using universal language mapping. Perhaps what’s more interesting is that, under proper assumptions on the structure of ![]() , the class of encoders and decoders we learn from, by using the traditional empirical risk minimization (ERM) framework to learn the language-dependent encoders and decoders on a small number of language pairs, we could expect the learned encoders/decoders to well generalize on unseen language pairs as well! Informally,
, the class of encoders and decoders we learn from, by using the traditional empirical risk minimization (ERM) framework to learn the language-dependent encoders and decoders on a small number of language pairs, we could expect the learned encoders/decoders to well generalize on unseen language pairs as well! Informally,
Theorem (informal): Let
be a connected graph where each node
corresponds to a language and each edge
means that the learner has been trained on language pair
and
, with empirical translation error
and corpus of size
. Then with high probability, for any pair of language
and
that are connected by a path
in
, its population level translation error is upper bounded by
.
In the theorem above, ![]() is some complexity measure of the class
is some complexity measure of the class ![]() . If we slightly simplify the theorem above by defining
. If we slightly simplify the theorem above by defining ![]() and realizing that the path length
and realizing that the path length ![]() is upper bounded by the diameter of the graph
is upper bounded by the diameter of the graph ![]() ,
, ![]() , we immediately obtain the following intuitive result:
, we immediately obtain the following intuitive result:
For any pair of languages
(the parallel corpus between
and
may not necessarily appear in our training corpora), the translation error between
and
is upper bounded by
.
The above corollary says that graphs ![]() that do not have long paths are preferable. For example,
that do not have long paths are preferable. For example, ![]() could be a star graph, where a central (high-resource) language acts as a pivot node. The proof of the theorem above essentially boils down to two steps: first, we use an epsilon-net argument to show that the learned encoders/decoders generalize on a pair of language that appears in our training corpora, and then by using the connectivity of the graph
could be a star graph, where a central (high-resource) language acts as a pivot node. The proof of the theorem above essentially boils down to two steps: first, we use an epsilon-net argument to show that the learned encoders/decoders generalize on a pair of language that appears in our training corpora, and then by using the connectivity of the graph ![]() , we apply a chain of triangle-like inequalities to bound the error along the path connecting any pair of languages.
, we apply a chain of triangle-like inequalities to bound the error along the path connecting any pair of languages.
Some Concluding Thoughts
The prospect of building a single system for universal machine translation is appealing. Compared with building a quadratic number of bilingual translators, such a single system is easier to train, build, deploy, and maintain. More importantly, this could potentially allow the system to transfer some common knowledge in translation from high-resource languages to low-resource ones. However, such promise often comes with a price, which calls for proper assumptions on the generative process of the parallel corpora used for training. Our paper takes a first step towards better understanding the tradeoff in this regard and proposes a simple setup that allows for zero-shot translation. On the other hand, there are still some gaps between theory and practice. For example, it would be interesting to see whether the BLEU score, a metric used in the empirical evaluation of translation quality, bears a similar kind of lower bound. Also, could we further extend our generative modeling of sentences so that there are more hierarchical structures in the semantic space ![]() ? Empirically, it would be interesting to implement the above generative model on synthetic data to see the actual performance of zero-shot translation under the model assumption. These challenging problems (and more) will require collaborative efforts from a wide range of research communities and we hope our initial efforts could inspire more efforts in bridging the gap.
? Empirically, it would be interesting to implement the above generative model on synthetic data to see the actual performance of zero-shot translation under the model assumption. These challenging problems (and more) will require collaborative efforts from a wide range of research communities and we hope our initial efforts could inspire more efforts in bridging the gap.
Reference
- Massively Multilingual Neural Machine Translation in the Wild: Findings and Challenges, Arivazhagan et al., https://arxiv.org/abs/1907.05019.
- Investigating Multilingual NMT Representations at Scale, Kudugunta et al., EMNLP 2019, https://arxiv.org/abs/1909.02197.
- On Learning Language-Invariant Representations for Universal Machine Translation, Zhao et al., ICML 2020, https://arxiv.org/abs/2008.04510.
- The Source-Target Domain Mismatch Problem in Machine Translation, Shen et al., https://arxiv.org/abs/1909.13151.
- How multilingual is Multilingual BERT? Pires et al., ACL 2019, https://arxiv.org/abs/1906.01502.
DISCLAIMER: All opinions expressed in this post are those of the author and do not represent the views of CMU.
This article was initially published on the ML@CMU blog and appears here with the authors’ permission.
.










