#NeurIPS2021 invited talks round-up: part two – benign overfitting, optimal transport, and human and machine intelligence

The 35th conference on Neural Information Processing Systems (NeurIPS2021) featured eight invited talks. Continuing our series of round-ups, we give a flavour of the next three presentations.

Benign overfitting

Peter Bartlett

In his talk, Peter focussed on the phenomenon of benign overfitting, one of the surprises to arise from deep learning: that deep neural networks seem to predict well, even with a perfect fit to noisy training data.

The presentation began with a broader perspective on theoretical progress inspired by large-scale machine learning problems. Peter took us back to 1988, and to a NeurIPS paper by Eric Baum and David Haussler who were interested in the question of generalization for neural networks. He then touched on overparameterization – the observation that neural networks with more parameters than the sample size can generalize well.

Moving on to benign overfitting, Peter reflected on what is surprising about this phenomenon. The fact that deep learning methods can provide accurate predictions when they fit perfectly to noisy data goes against the statistical wisdom that you find in textbooks. The guidance given when teaching undergraduate students has typically been that you don’t want to fit the data too well otherwise you’re unlikely to predict accurately.

In his research, Peter has considered linear regression, and the phenomenon of benign overfitting in that setting. He presented his, and his collaborators’, theorem to characterise this overfitting. You can see the overview of that theorem in the figure below. The intuition behind why we observe benign overfitting is that it is due to the pattern of the eigenvalues, in other words, the mix of eigenvalues of the covariance matrix and the relative levels of variance in different directions in the input space. To avoid harming the prediction accuracy, the noise energy must be distributed across many unimportant directions. Therefore, overparameterization is essential – we need more unimportant directions than samples.

Screenshot from Peter’s talk.

Peter also talked about adversarial samples, and the fact that benign overfitting leads to huge sensitivity to adversarial perturbations. He also showed that his method can be extended to ridge regression.

Optimal transport: past, present, and future

Alessio Figalli

The theory of optimal transport was formalised by Gaspard Monge more than 200 years ago. The problem is as follows: imagine that you have a certain amount of material to extract from the ground and to transport to different locations for building work. Considering each measure of material, to which destination should it be sent to guarantee the constructions can be built whilst minimising the total transportation cost? In his problem, Monge used the total distance covered to measure the transportation cost.

It was only much later, the 1940s, that there was further significant work in this field, in the form of Leonid Kantorovich’s formulation that allowed for non-deterministic transport. The next fundamental breakthrough arrived in the 1980s, with work from Brenier, and Rachev and Rüschendorf ensuring that optimal transport became a problem that was fully embraced by the mathematical community.

The theory has found numerous applications in areas such as urban planning, meteorology, statistics, engineering design, biology, and finance, to name a few. It has also become a powerful tool in machine learning, and Alessio gave some examples, one of which we summarise below.

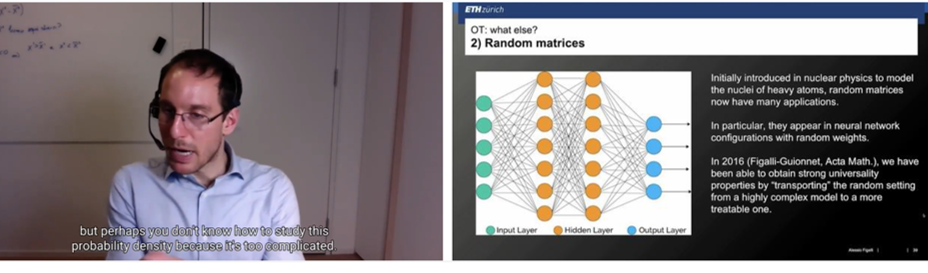
Initially introduced in nuclear physics to model the nuclei of heavy atoms, random matrices now have many applications. In particular, when it comes to neural networks, they are used to build configurations where random weights are used. The kind of question you have in random matrix theory is: as the size of the matrix goes to infinity, you’d like to understand properties of the eigenvalues (how they behave, how they fluctuate, for example). There are theorems in random matrix theory that tell us that as the number of dimensions of these matrices goes to infinity, you have a universality problem. In other words, you see the same behaviour even if the matrices were different at finite scale, the infinite dimension phenomenon makes them behave in a universal way. In 2016, Alessio and colleagues proved universality properties for random matrices using transport maps to “transport” the properties of a complex model to a more simple one. The transport maps can be used to infer properties of the complex matrices random matrices.

Screenshot from Alessio’s talk.

A conversation on human and machine intelligence

Daniel Kahneman

The session began with Daniel sharing his view on judgement, which is that the principles of perception extend to basic cognition. He used the line drawing diagram of a cube (which you can perceive in two different orientations) to demonstrate that we deal not with reality directly, but with reality as a representation. There is choice in the representation. For example, in this representation there is a choice between seeing the cube in one orientation, and the other. The twelve lines on the page that form the diagram have different roles depending on the orientation of the cube.

Moving on to another example, Daniel talked about the slide below. Looking at the A B C and the 12, 13, 14, the B and the 13 are actually exactly the same. This demonstrates the coherence of the interpretation – in the context letters the information is viewed as a letter, but in the context of numbers exactly the same stimulus is viewed as a number. If you are just shown the three letters, the idea that you could view the B as a 13 never occurs to you, because the ambiguity is completely suppressed.
Screenshot from Daniel’s talk.

The way Daniel sees it those are ideas that are common to perception and to cognition. We operate on a representation that we form, that has a certain coherence.

Following the introduction, there followed an in-depth conversation with Josh Tenenbaum. The pair discussed topics ranging from so-called rational thinking, the model behind AlphaGo, system one and system two, AI researchers learning from psychology, and computer vision.

Daniel mentioned that someone had asked him what a modern Turing test would look like. He said that it might be a system that can avoid absurd mistakes. It would make the kind of mistakes that humans make, but it wouldn’t make the kind of mistakes that people find funny or absurd. He wondered whether there was a finite list of types absurd mistakes, and if it might be interesting to work through such a list and construct a system that avoids certain mistakes. He and Josh discussed this in the context of computer vision, and how recognising the types of common mistakes the systems make can advance the research.

Read our round-up of the first three invited talks from NeurIPS here.

Lucy Smith , Managing Editor for AIhub.

Lucy Smith , Managing Editor for AIhub.