ΑΙhub.org
Algorithmically finding ways to synthesize new medicine
Image created using DALL-E with the prompt “Games, Chemistry, Artificial Intelligence”.
In modern pharmaceutical research, active ingredients are designed using a computer. Only in a second step, one determines, still away from the wet lab, whether these complex molecules can actually be synthesized. This is considered a true art among chemists as it is highly complex and requires a broad knowledge of chemical reactions. At the pharmaceutical company Bayer, one uses a time-intensive Artificial Neural Network (ANN) to predict which reactions could immediately produce the candidate at hand. Typically, the reactants required for the proposed reactions are still quite complex, so one has to call the ANN again on such reactants, then on the reactants required for the resulting reactions, and so on. Eventually, one has hopefully found a synthesis plan, which only requires simple, buyable molecules to start with. A synthesis plan can be viewed as a tree, see Figure 1. The process of recursively splitting up the target molecule is called retrosynthesis.
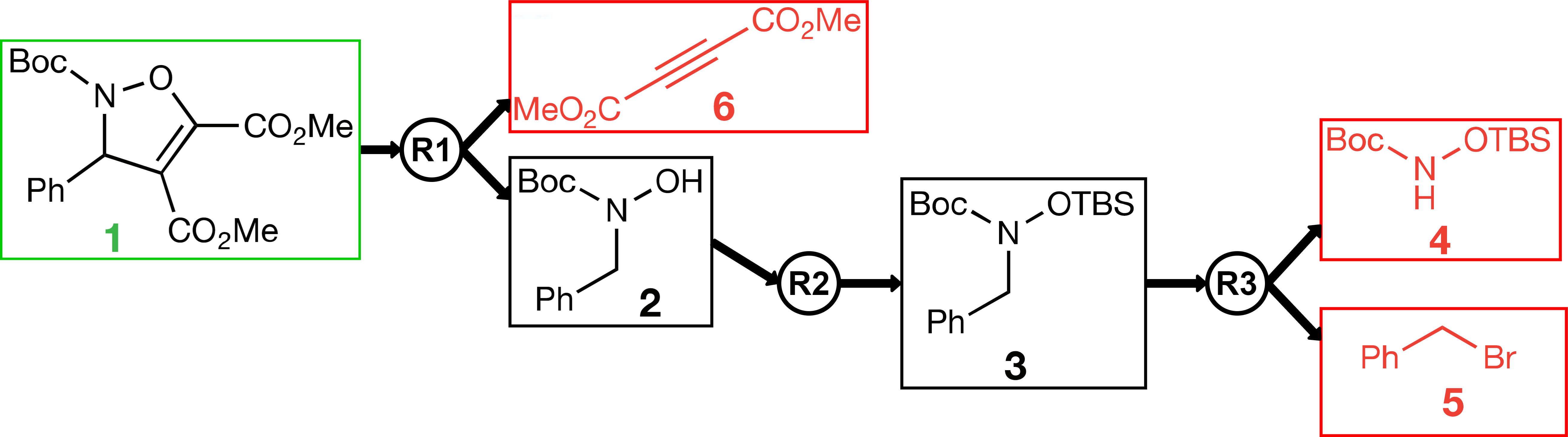Figure 1. Retrosynthetic plan of the molecule inside the green borders. R1, R2, and R3 are reactions that produce the molecule on the left side with the reactants on the right of the reaction.
The central algorithmic question that arises is how to decide on which molecules to call the ANN again, so as to optimally utilize the computation time. Suppose R and S are only two of the reactions immediately leading to the target molecule. Should one rather explore a reactant of a reaction that only produces a reactant of R—a reaction that was promising to start with, but which has proven to require not that easily synthesizable reactants? Or should one rather switch to exploring the unexplored reaction S that requires many different reactants? To make things more complicated, a single molecule may serve as a reactant in several reactions.
A class of algorithms that can be used to answer the above questions are the Proof-Number Search (Allis et al., 1994) and its variants. The Proof-Number Search was originally designed to solve two-player games such as Go and Chess, but it can, using an interesting connection between such games and retrosynthesis described later, also be applied to the latter. Our paper (Franz et al., 2022) shows that a particular fast algorithm from this class eventually finds a solution if one exists, thereby solving a problem that was open for over ten years. Further, we improve the classes’ usability for retrosynthesis by adapting it so that it computes a set of diverse synthesis plans (rather than a single one, or a set of similar synthesis paths), which can then be proposed to chemists to pick from.
Connection between retrosynthesis and two-player games
Consider the following two-player game: The so-called reaction player and the so-called molecule player alternatingly pick reactions and molecules, respectively, starting with the molecule player picking the target molecule. From then on, the reaction player always picks a reaction that (according to the ANN) leads to the just-picked molecule, and the molecule player always picks a molecule that is a reactant of the just-picked reaction. The reaction player wins whenever the molecule player eventually has to pick a buyable molecule; the molecule player wins if that is never the case. This defines the rules of the game.
It is not difficult to see that the reaction player can always win if there is a synthesis plan for the target molecule (according to the reactions from the ANN): The reaction player can always select a reaction that is used in that synthesis plan, forcing the molecule player to also pick a molecule that is used in the same synthesis plan, which will eventually be a buyable molecule. Conversely, if there is no such synthesis plan, the molecule player can make sure that the reaction player never wins: The molecule player can always pick a non-synthesizable molecule. In the beginning, the player does so by the rules. The reaction player then always has to select a reaction for which at least one reactant is not synthesizable (otherwise the reaction’s product would be synthesizable), which the molecule player can pick.
The previous discussion establishes the connection between retrosynthesis and two-player games: There is a winning strategy for the reaction player exactly when a synthesis plan for the target molecule exists. In fact, computing a winning strategy for the two-player game can be seen to be equivalent to computing a synthesis plan for the target molecule.
Two-player games
More generally and formally, in a two-player game, there are two players, Player 1 and 2, who play on a so-called AND/OR graph. The game starts at the so-called root, and it moves along the (directed) edges of the graph. The graph consists of two types of nodes, OR nodes, from which Player 1 may move next, and AND nodes, from which Player 2 may move next. The nodes without outgoing edges (terminal nodes) are known to be a victory for one of the players, and a victory can also be triggered by repeating a node. Using the facts that Player 1:
- can win from an OR node at least of whose outgoing edges lead to a victory
- wins from an AND node of which all outgoing edges lead to a victory
as well as the corresponding statements for Player 2, we can determine for additional nodes, and eventually the root, which Player can win from there, see Figure 2.
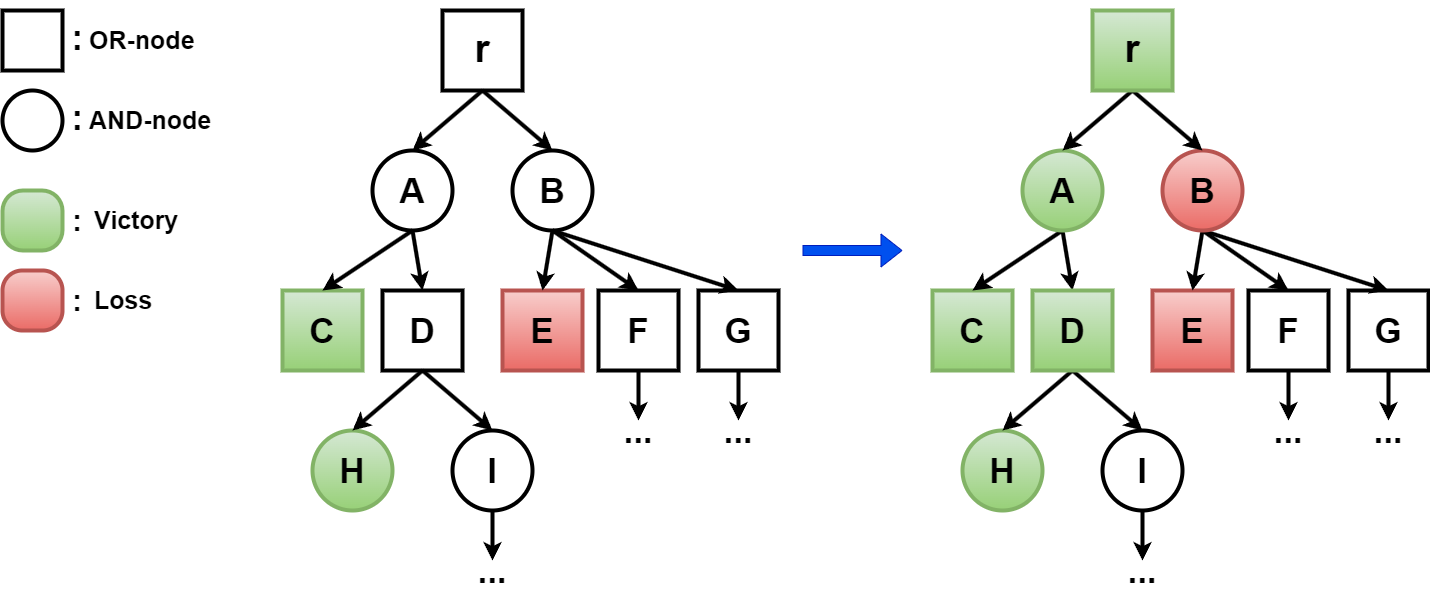Figure 2. Example of a part of an AND/OR-graph, with the outcome of the game shown on the right.
Naively computing winning strategies in this way requires explicitly representing the whole graph, which is often impossible, considering the extremely large number of states in games like Chess or Go. Therefore, many algorithms use heuristics to identify parts of the graph in which the probability of finding a winning strategy is higher. One of these algorithms is the aforementioned Proof-Number Search as well as the popular variant Depth-First Proof-Number Search (DFPN) (Nagai, 2002).
Completeness and soundness
Clearly, one wants the algorithm to always find a winning strategy if there exists one, in which case we call it complete. Conversely, one also wants the algorithm to not output strategies that are not winning, in which case we call it sound. It is known that the DFPN is complete and sound on graphs not containing cycles, called acyclic graphs (Kishimoto & Müller, 2008). In the same paper, however, the authors provided a cyclic graph on which DFPN is not complete. In our paper, we provide a simpler such graph. To combat the issue of incompleteness, the Threshold Controlling Algorithm (TCA), a subroutine to be used in DFPN, was proposed twelve years ago (Kishimoto, 2010).
Still, the conjecture that DFPN with TCA is complete on cyclic graphs has remained unproven. One part of our contribution is proving precisely this conjecture. Assuming that the algorithm is not complete on some graph, we isolate a certain critical part of the graph, which may be cyclic but for which we can establish properties that are not necessarily fulfilled in general cyclic graphs. Using these properties, we can then reuse parts of the proof for acyclic graphs to obtain a contradiction to the initial assumption; for more details, see Section 3 in our paper. Now, one can be sure that, if there exists a winning strategy in an AND/OR-graph, DFPN with TCA will eventually find such a strategy.
New algorithm: DFPN* and Evaluation
The second part of our contribution is the DFPN* algorithm, which can traverse the chemical synthesis space. Here, we add to existing approaches the possibility of obtaining multiple diverse solutions for a single target molecule, such that a chemist can choose their favourite plan, by looking at properties such as costs and risk. We do so by re-running the algorithm after a synthesis plan, or several plans, were already found, but this time neglecting certain reactions that were used in previously found synthesis plans.
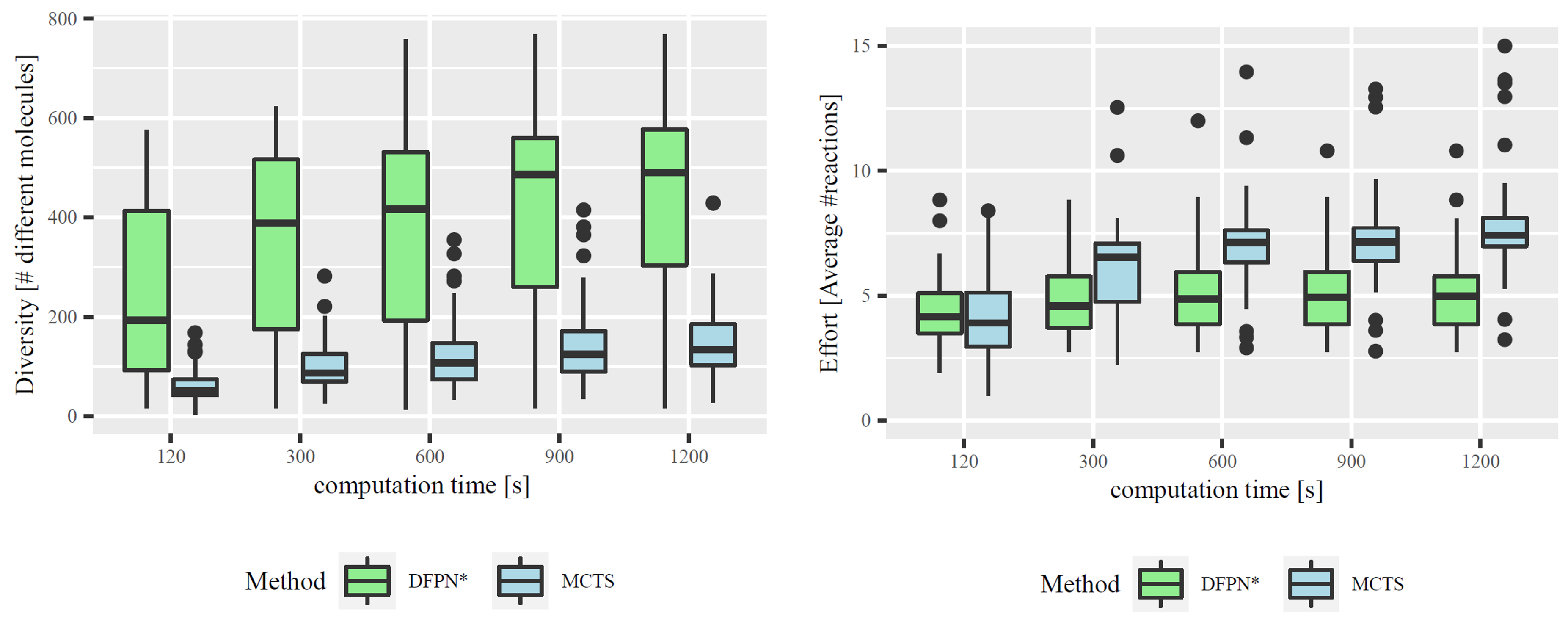Figure 3. Left: Comparison of Diversity. Distributions of the mean total number of intermediate molecules per solved target molecule. Right: Comparison of Synthesis Effort. Distributions of the mean number of reactions per synthesis plan for each solved target molecule.
In our paper, we compare DFPN* with the most commonly used algorithm for retrosynthesis, Monte-Carlo Tree Search (MCTS) (e.g., Segler et al., 2018) which naturally produces a set of synthesis plans. In fact, on average, MCTS found more plans than DFPN*. However, employing the number of different intermediate molecules across the various plans as a measure for diversity, we were able to show that DFPN* provides significantly more diverse plans than MCTS; see the left part of Figure 3. Furthermore, the plans found by MCTS tend to be longer and thus typically more difficult; see the right part of Figure 3.
References
- L. V. Allis, M. van der Meulen, and H. J. van den Herik. Proof-number search. Artificial Intelligence, 66(1), pages 91–124, 1994.
- C. Franz, G. Mogk, T. Mrziglod, K. Schewior. Completeness and Diversity in Depth-First Proof-Number Search with Applications to Retrosynthesis. In International Joint Conference on Artificial Intelligence (IJCAI), pages 4747-4753, 2022.
- A. Nagai. Df-pn algorithm for searching AND/OR trees and its applications. PhD thesis, Department of Information Science, University of Tokyo, 2002.
- A.Kishimoto and M. Müller. About the completeness of depth first proof number search. In Computers and Games, pages 146-156, 2008.
- A. Kishimoto. Dealing with infinite loops, underestimation, and overestimation of depth-first proof-number search. In AAAI Conference on Artificial Intelligence (AAAI), pages 108-113, 2010.
- M. H. S. Segler, M. Preuss, M. P. Waller, Planning Chemical Syntheses with Deep Neural Networks and Symbolic AI, Nature 555, pp. 604-610, 2018.
This work won a distinguished paper award at IJCAI 2022.
tags: IJCAI2022
AIhub is supported by:
