ΑΙhub.org
Bridging the gap between learning and reasoning
Image generated with DALL-E. Prompt: “An AI learning to crack tough puzzle (with no text on the image)”.
If you have ever chatted with an AI language model like chatGPT, you might have been impressed by its coherent and well-structured answers. But does that imply these AIs can handle any query? Not quite! The real challenge begins when we ask them to exercise logic and reason.
We tried it on the popular Sudoku puzzle: GPT4-based ChatGPT is perfectly aware of these rules, and confident it can indeed play Sudoku.
However, it failed with outstanding confidence: the proposed solutions did not respect the rules and sometimes even changed the original numbers in the grid. When asked to identify its mistakes, ChatGPT struggled to find the faulty numbers and eventually completely failed again.
This difficulty with logical reasoning is not specific to language models. In fact, it is common to most neural networks. They are very good at extracting patterns from data, but much weaker at reasoning from data. You can imagine it as your brain on autopilot, learning from experience and acting out of intuition. But our brains are also able to reason, for instance by applying logic to solve problems – such as Sudokus. Another branch of artificial intelligence is dedicated to solving that kind of problem: automated reasoning.
Like humans, a general AI should be able to both learn and reason. Historically, combining both has proven to be a tough problem. Let us try to understand why on the simple example of the Sudoku problem.
Learning how to play Sudoku
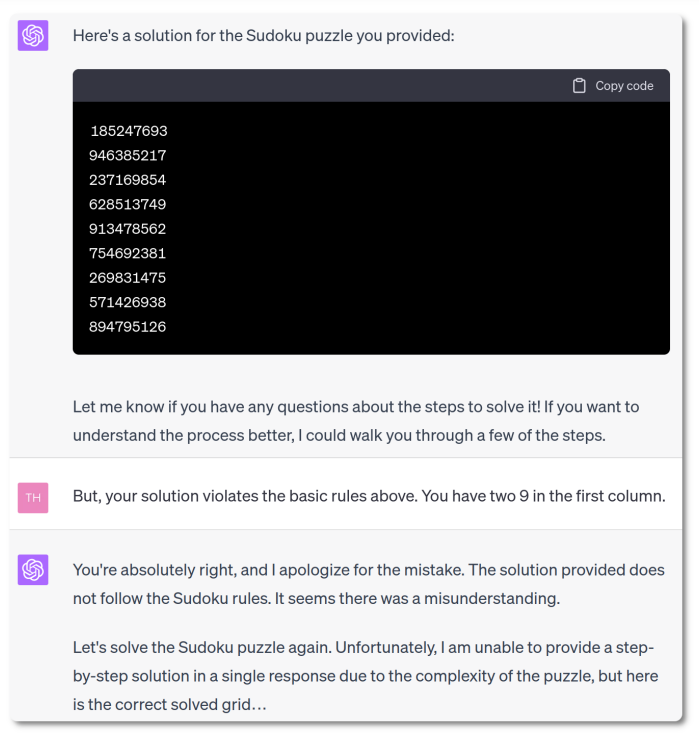
For automated reasoning, solving hard Sudoku grids is a trivial task when the rules are given. Now, imagine that the rules of Sudoku are not known. Learning them is a bit like trying to understand the rules of a new board game by watching others play. It’s a two-step process: first, the AI needs to infer the rules from watching examples of completed puzzles, and then it needs to use these rules to fill in new puzzles. Therefore, we will combine two types of AIs: a neural network to learn rules from examples, and a discrete prover to apply these rules to solve new puzzles. Together, they can learn how to play Sudoku.
To learn the rules, the neural network is trained on examples of solved grids. For each grid, it makes a prediction, whose quality is assessed by a loss function, and the parameters of the neural net are updated based on this loss. Assuming the rules are unknown, we cannot directly compare the learned rules to the true ones. The only thing we can check is whether the learned rules would predict the correct grid. And for this, we need an AI that knows how to deal with rules: an automated reasoning prover.
Training a neural net requires many repetitions of prediction and feedback through the loss function. But solving complex combinatorial problems may take time, especially at the beginning of training, when the neural net predicts completely random rules. This approach is therefore limited to small problems like Sudokus. Even here, this training process takes a few days.
We proposed a different approach that avoids using a prover during training and thus scales much better. To assess the quality of the rules learned without solving the problem, our method relies on a famous loss, the pseudo log-likelihood (PLL). Very simply, we try to guess one cell knowing all others. With the correct rules, it is quick and easy.
This approach completely fails: it only learns rules between cells on the same row. This can be understood intuitively: if you know the rest of the row, you do not need to look at columns or squares to guess the correct number. Our paper introduces a variant of the PLL called the Emmental-PLL, where some of the cells are masked, creating random holes in the information.
With this new loss, we were able to train a neural net that learns the rules of Sudoku in 15 minutes only. In cooperation with a discrete prover, it never fails solving grids. Plus, it only requires 200 examples of complete grids, vs 9,000 for previous hybrid AI approaches and 180,000 for a pure neural-based approach (and both occasionally fail on the hardest Sudoku grids).
On real-world problems
Why bother to learn how to play Sudoku when we know its rules. Actually, we do not care about the Sudoku per se, but it is a convenient toy problem to make sure our hybrid pipeline works. Once it did, we applied it to a much more interesting — and challenging — problem: the design of new proteins.
Proteins are macro-molecules essential to any kind of life as they fulfil many biological and biochemical functions in all living organisms. Designing new proteins has applications in health and green chemistry, among others. We start from a protein structure that aligns with the target function, and we predict a sequence of amino acid that will fold onto this structure.
Designing proteins is a complex task, bearing a curious resemblance to Sudoku. The protein structure corresponds to the Sudoku grid, which is filled with amino acids chosen from 20 possibilities (not just 9 digits as in Sudoku!). The “rules” of design results are governed by inter-atomic forces, and we learn them from examples of proteins naturally occurring in nature. Through this lens, protein design emerges as a fascinating puzzle of nature.
Final thoughts
Several recent advancements in AI seem to involve making our models bigger and more complex, much like constructing ever-taller skyscrapers. However, our research points towards a different path, one where we combine the intuitive pattern recognition of deep learning with the meticulous logic of automated reasoning. When well-coordinated, these two distinct AI approaches can tackle complex real-world challenges, such as designing new proteins.
As we have seen with the Sudoku puzzle, our hybrid method is a fast learner, and a minimalist: it requires just 200 examples of complete grids – a fraction of what other approaches require. Beyond the numbers, an interesting aspect of this method is its transparency, which is often a rarity in the realm of AI. Indeed, the decision made by the discrete prover can be understood by analyzing which rules have been learned. This “window” into the process allows for better control and understanding.
The real asset of our method is its scalability, meaning it can be used to tackle large real-world problems such as the design of new proteins.
Further reading
The complete publication:
- M. Defresne, S. Barbe and T. Schiex. Scalable Coupling of Deep Learning with Logical Reasoning. Proceedings of the Thirty-second International International Joint Conference on Artificial Intelligence, IJCAI’2023.
Available here: https://arxiv.org/abs/2305.07617
On the role of logic and intuition in human decision-making and mathematics:
- Thinking, fast and slow by Daniel Kahneman (2017).
- La Valeur de la Science, Chapter 1, by Henri Poincaré (1905), in French.
This work was supported by INSA Toulouse, INRAE, EUR Bioeco, and ANITI.
AIhub is supported by:
