Generating 3D molecular conformers via equivariant coarse-graining and aggregated attention

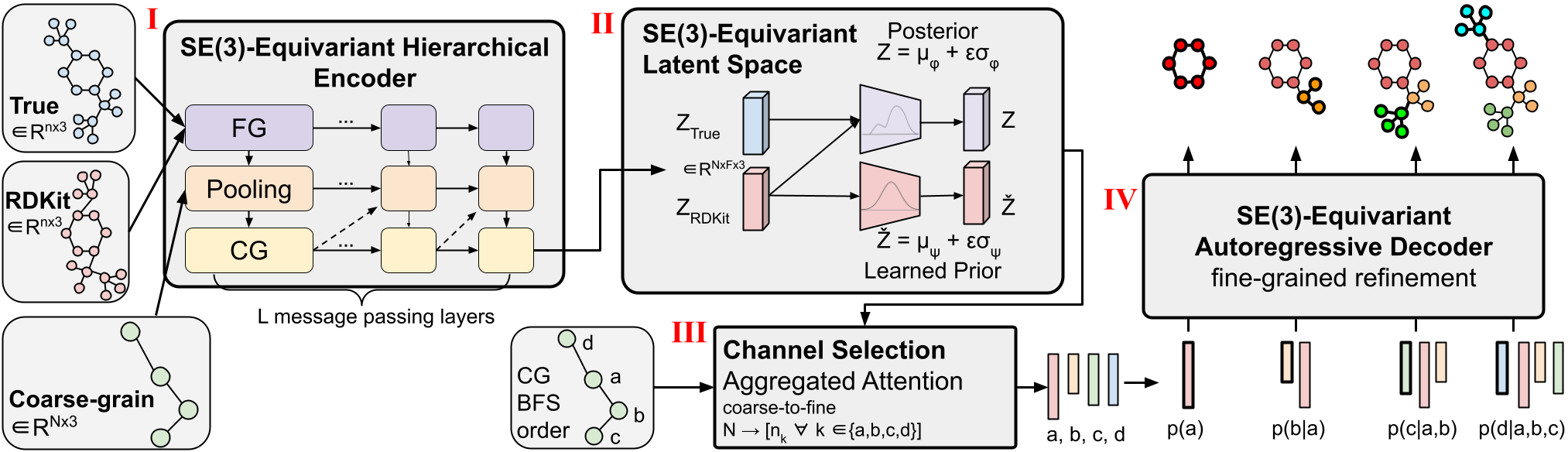Figure 1: CoarsenConf architecture.

By Danny Reidenbach and Aditi S. Krishnapriyan

Molecular conformer generation is a fundamental task in computational chemistry. The objective is to predict stable low-energy 3D molecular structures, known as conformers, given the 2D molecule. Accurate molecular conformations are crucial for various applications that depend on precise spatial and geometric qualities, including drug discovery and protein docking.

We introduce CoarsenConf, an SE(3)-equivariant hierarchical variational autoencoder (VAE) that pools information from fine-grain atomic coordinates to a coarse-grain subgraph level representation for efficient autoregressive conformer generation.

Background

Coarse-graining reduces the dimensionality of the problem allowing conditional autoregressive generation rather than generating all coordinates independently, as done in prior work. By directly conditioning on the 3D coordinates of prior generated subgraphs, our model better generalizes across chemically and spatially similar subgraphs. This mimics the underlying molecular synthesis process, where small functional units bond together to form large drug-like molecules. Unlike prior methods, CoarsenConf generates low-energy conformers with the ability to model atomic coordinates, distances, and torsion angles directly.

The CoarsenConf architecture can be broken into the following components:
(I) The encoder takes the fine-grained (FG) ground truth conformer , RDKit approximate conformer , and coarse-grained (CG) conformer as inputs (derived from and a predefined CG strategy), and outputs a variable-length equivariant CG representation via equivariant message passing and point convolutions.
(II) Equivariant MLPs are applied to learn the mean and log variance of both the posterior and prior distributions.
(III) The posterior (training) or prior (inference) is sampled and fed into the Channel Selection module, where an attention layer is used to learn the optimal pathway from CG to FG structure.
(IV) Given the FG latent vector and the RDKit approximation, the decoder learns to recover the low-energy FG structure through autoregressive equivariant message passing. The entire model can be trained end-to-end by optimizing the KL divergence of latent distributions and reconstruction error of generated conformers.

MCG task formalism

We formalize the task of Molecular Conformer Generation (MCG) as modeling the conditional distribution , where is the RDKit generated approximate conformer and is the optimal low-energy conformer(s). RDKit, a commonly used Cheminformatics library, uses a cheap distance geometry-based algorithm, followed by an inexpensive physics-based optimization, to achieve reasonable conformer approximations.

Coarse-graining

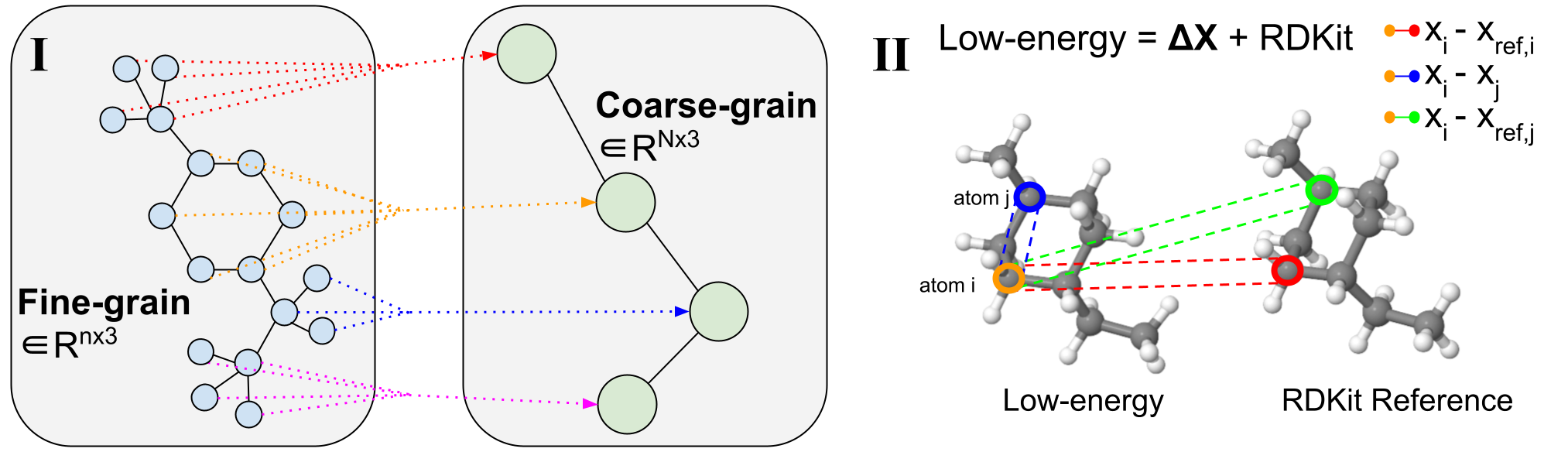Figure 2: Coarse-graining Procedure.
(I) Example of variable-length coarse-graining. Fine-grain molecules are split along rotatable bonds that define torsion angles. They are then coarse-grained to reduce the dimensionality and learn a subgraph-level latent distribution. (II) Visualization of a 3D conformer. Specific atom pairs are highlighted for decoder message-passing operations.

Molecular coarse-graining simplifies a molecule representation by grouping the fine-grained (FG) atoms in the original structure into individual coarse-grained (CG) beads with a rule-based mapping, as shown in Figure 2(I). Coarse-graining has been widely utilized in protein and molecular design, and analogously fragment-level or subgraph-level generation has proven to be highly valuable in diverse 2D molecule design tasks. Breaking down generative problems into smaller pieces is an approach that can be applied to several 3D molecule tasks and provides a natural dimensionality reduction to enable working with large complex systems.

We note that compared to prior works that focus on fixed-length CG strategies where each molecule is represented with a fixed resolution of CG beads, our method uses variable-length CG for its flexibility and ability to support any choice of coarse-graining technique. This means that a single CoarsenConf model can generalize to any coarse-grained resolution as input molecules can map to any number of CG beads. In our case, the atoms consisting of each connected component resulting from severing all rotatable bonds are coarsened into a single bead. This choice in CG procedure implicitly forces the model to learn over torsion angles, as well as atomic coordinates and inter-atomic distances. In our experiments, we use GEOM-QM9 and GEOM-DRUGS, which on average, possess 11 atoms and 3 CG beads, and 44 atoms and 9 CG beads, respectively.

SE(3)-equivariance

A key aspect when working with 3D structures is maintaining appropriate equivariance.
Three-dimensional molecules are equivariant under rotations and translations, or SE(3)-equivariance. We enforce SE(3)-equivariance in the encoder, decoder, and the latent space of our probabilistic model CoarsenConf. As a result, remains unchanged for any rototranslation of the approximate conformer . Furthermore, if is rotated clockwise by 90°, we expect the optimal to exhibit the same rotation. For an in-depth definition and discussion on the methods of maintaining equivariance, please see the full paper.

Aggregated attention

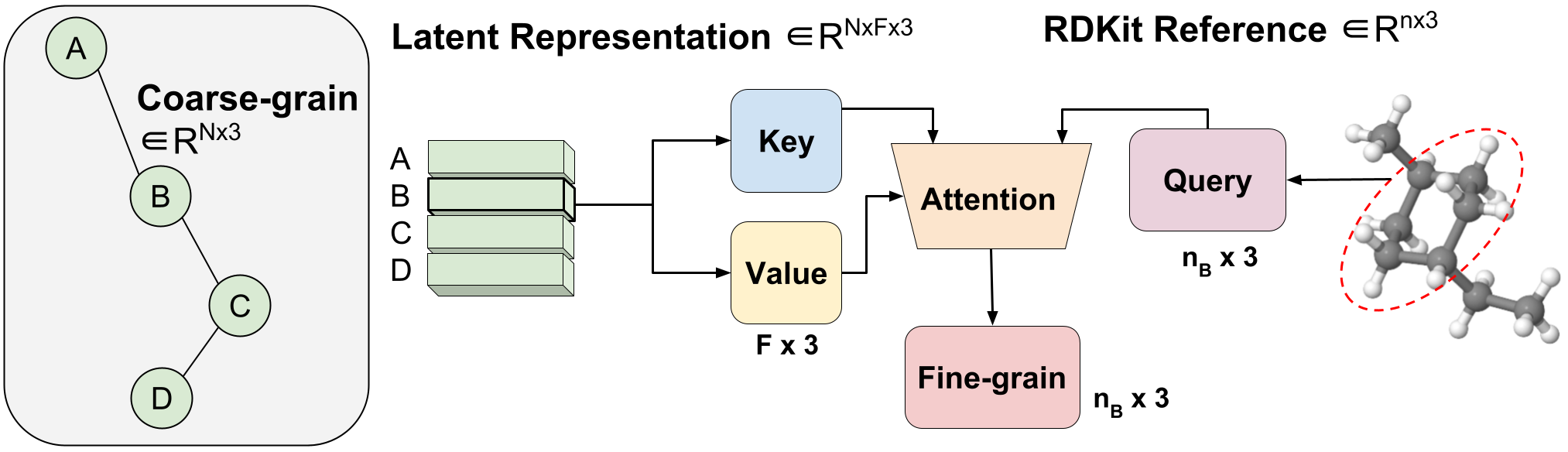Figure 3: Variable-length coarse-to-fine backmapping via Aggregated Attention.

We introduce a method, which we call Aggregated Attention, to learn the optimal variable length mapping from the latent CG representation to FG coordinates. This is a variable-length operation as a single molecule with atoms can map to any number of CG beads (each bead is represented by a single latent vector). The latent vector of a single CG bead is used as the key and value of a single head attention operation with an embedding dimension of three to match the x, y, z coordinates. The query vector is the subset of the RDKit conformer corresponding to bead , where is variable-length as we know a priori how many FG atoms correspond to a certain CG bead. Leveraging attention, we efficiently learn the optimal blending of latent features for FG reconstruction. We call this Aggregated Attention because it aggregates 3D segments of FG information to form our latent query. Aggregated Attention is responsible for the efficient translation from the latent CG representation to viable FG coordinates (Figure 1(III)).

Model

CoarsenConf is a hierarchical VAE with an SE(3)-equivariant encoder and decoder. The encoder operates over SE(3)-invariant atom features , and SE(3)-equivariant atomistic coordinates . A single encoder layer is composed of three modules: fine-grained, pooling, and coarse-grained. Full equations for each module can be found in the full paper. The encoder produces a final equivariant CG tensor , where is the number of beads, and F is the user-defined latent size.

The role of the decoder is two-fold. The first is to convert the latent coarsened representation back into FG space through a process we call channel selection, which leverages Aggregated Attention. The second is to refine the fine-grained representation autoregressively to generate the final low-energy coordinates (Figure 1 (IV)).

We emphasize that by coarse-graining by torsion angle connectivity, our model learns the optimal torsion angles in an unsupervised manner as the conditional input to the decoder is not aligned. CoarsenConf ensures each next generated subgraph is rotated properly to achieve a low coordinate and distance error.

Experimental results

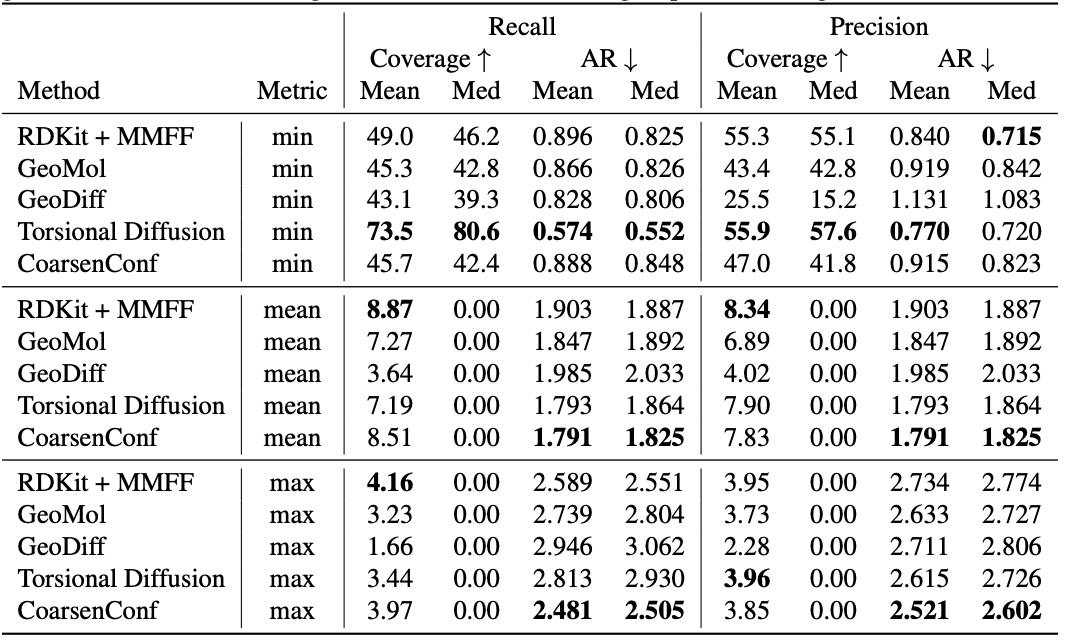Table 1: Quality of generated conformer ensembles for the GEOM-DRUGS test set () in terms of Coverage (%) and Average RMSD (). CoarsenConf (5 epochs) was restricted to using 7.3% of the data used by Torsional Diffusion (250 epochs) to exemplify a low-compute and data-constrained regime.

The average error (AR) is the key metric that measures the average RMSD for the generated molecules of the appropriate test set. Coverage measures the percentage of molecules that can be generated within a specific error threshold (). We introduce the mean and max metrics to better assess robust generation and avoid the sampling bias of the min metric. We emphasize that the min metric produces intangible results, as unless the optimal conformer is known a priori, there is no way to know which of the 2L generated conformers for a single molecule is best. Table 1 shows that CoarsenConf generates the lowest average and worst-case error across the entire test set of DRUGS molecules. We further show that RDKit, with an inexpensive physics-based optimization (MMFF), achieves better coverage than most deep learning-based methods. For formal definitions of the metrics and further discussions, please see the full paper linked below.

For more details about CoarsenConf, read the paper on arXiv.

BibTex

If CoarsenConf inspires your work, please consider citing it with:

@article{reidenbach2023coarsenconf,
      title={CoarsenConf: Equivariant Coarsening with Aggregated Attention for Molecular Conformer Generation},
      author={Danny Reidenbach and Aditi S. Krishnapriyan},
      journal={arXiv preprint arXiv:2306.14852},
      year={2023},
}

This article was initially published on the BAIR blog, and appears here with the authors’ permission.

BAIR blog

BAIR blog