
ΑΙhub.org
Generating physically-consistent local-scale climate change projections
Imagine a farmer in charge of several fruit crops located over a small village in the Spanish countryside. He is worried about the increasing temperature, especially under climate change conditions, as this could have devastating effects on his crops in the future. The only tools available to inform the farmer about the evolution of climate in future scenarios are climate models, which are numerical models simulating the dynamics of climate. However, due to computational and physical limitations, the simulations of these models have very low resolution, spanning hundreds of kilometers, so the farmer has no specific information for the region spanning his crops.
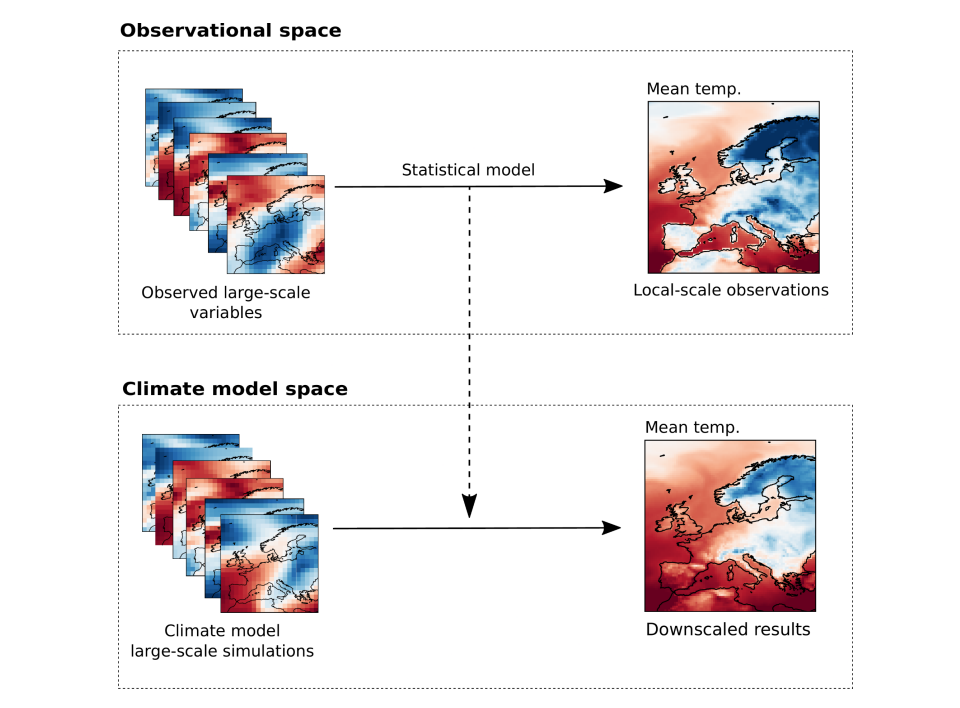
A popular technique to overcome this limitation is statistical downscaling (SD), which consists of learning a statistical model to map from the coarse resolution of climate models to the demanded local-scale. There exist several ways of performing this SD. We focus on the so-called perfect prognosis approach, which learns the mapping between large-scale variables (for example, humidity and winds) and the demanded local-scale variable (for example, mean temperature) on actual measurements (observational data) and then applies it to the simulations of the climate models. This approach can generate local-scale simulations in future scenarios. In the following figure we show a schematic view of the perfect prognosis SD of the mean temperature.

Recently, deep learning (DL) has emerged as a promising SD method, as these techniques possess an outstanding ability to learn patterns from spatial-temporal data, such as the data we find in typical SD applications. The most common workflow for downscaling these variables with DL involves training a different model for each variable. For instance, to downscale the minimum, mean and maximum temperature (three different variables) researchers generally train three different DL models. However, the climate is a highly complex system, and the variables involved are closely related to each other by physical links. By relying on this independent modeling, we are breaking the dependency between the downscaled variables, potentially leading to violations of basic physical constraints.
For instance, imagine that the aforementioned farmer has decided to rely on SD for obtaining information about the evolution of the minimum, mean and maximum temperature, as some fruits are sensitive to the interdiurnal temperature variation. Since the DL models generating the local-scale version of these variables are independent, the farmer gets odd results. For instance, for some days in the future, he gets a minimum temperature higher than the maximum. This would invalidate the practical application of these local-scale projections and would lead the farmer to not trust the SD-generated simulations.
In our work, presented in the AAAI 2023 Fall Symposium, we explore the violations of these physical constraints for the specific case of the SD of minimum, mean and maximum temperature and lay the foundation for a physically-consistent framework for downscaling these variables. This framework encompasses training a unique DL model for the three variables, while forcing the downscaled variables to specifically fulfil the following constraint:
Tmin <= TMean <= Tmax
where Tmin, Tmean and Tmax correspond to minimum, mean and maximum temperature, respectively. In the following figure we show a schematic view of the proposed framework.
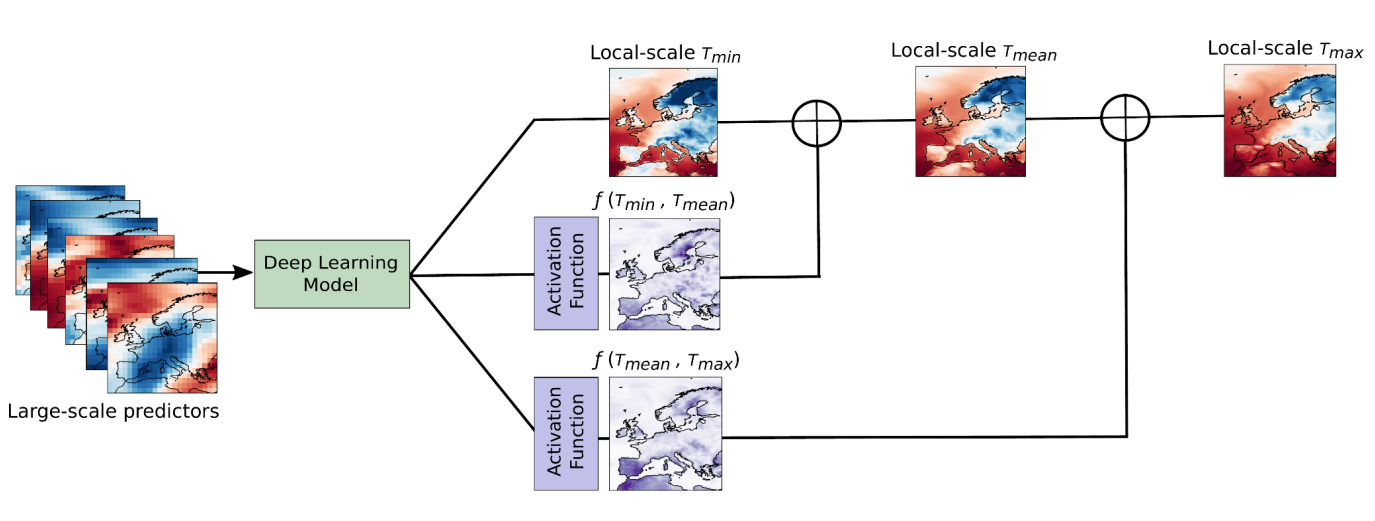
Within this framework, we train a unique DL model that takes the set of large-scale variables as inputs (recall that we work within the perfect prognosis approach) and outputs three quantities: one, the minimum temperature; two what we need to add to the minimum temperature to get the mean; and three, what we need to add to the mean to get the maximum temperature. This procedure allows us to enforce the physical constraints in the architecture of the DL model, so there is no way the resultant high-resolution simulations violate the aforementioned constraint. To assess the efficacy of the proposed framework, we downscaled the aforementioned three variables through three different models:
- Single modeling: a different DL model per variable.
- Shared modeling: a unique multi-variable DL model for the three variables.
- Framework modeling: our proposed framework described above.
For each experiment, and following the perfect prognosis approach, first we train the model in the observational space and then we downscale in future scenarios from a climate model. In the following figure, we show the annual percentage of violations of the physical constraint to fulfil, for the single and shared experiment, both in the observational and the climate model space.
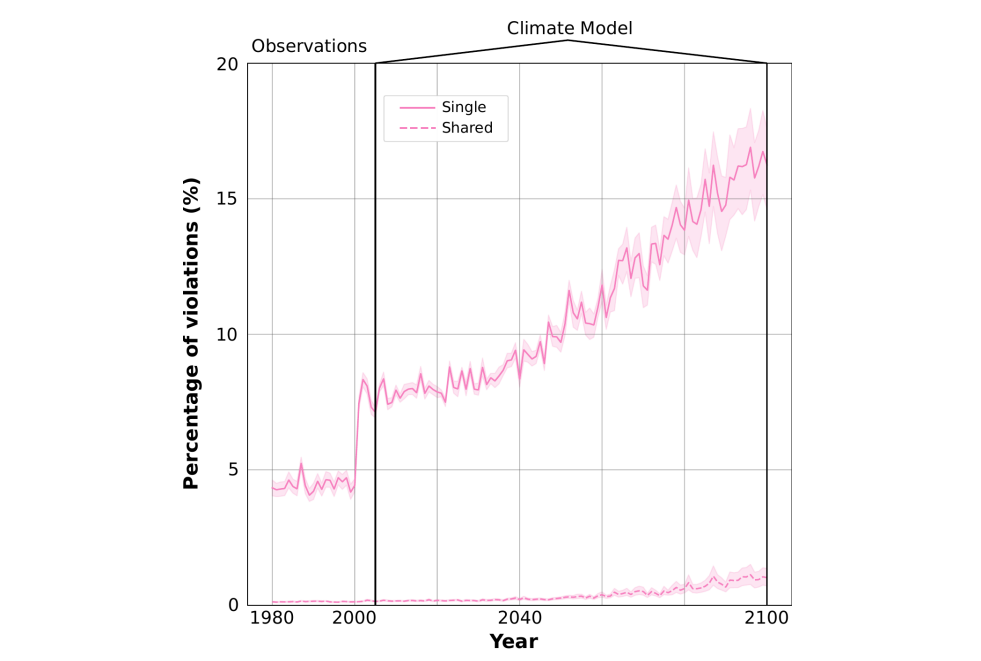
We do not show the results for the proposed framework, as by construction the percentage of violations is zero. With the single-model approach, which is the most commonly used so far, we observe a significant number of violations, especially as we move forward in time, especially when downscaling from the climate model. The shared model also displays a number of violations with an increasing trend in time, although much lower than the single model.
Obviously, it is expected to get a high number of violations when downscaling the three variables independently, since as we have discussed above, we ignore the inherent relationship between them. Modeling the three variables simultaneously helps reduce the number of violations, although still the model can commit them, especially when downscaling from the global climate models in future scenarios. This improvement may be caused by the multi-task nature of the shared model, which forces the DL model to learn a more robust and physically-based representation. However, if we want to be sure that no violations occur, we need to rely on a framework such as the one proposed in our work.
Overall, in our work we show how typical DL-based SD approaches incur a large number of violations of physical constraints, especially when downscaling in future scenarios. To alleviate this we lay the foundations for a framework encoding these constraints, thus allowing for more physically-consistent DL models. This research is key if we want to build trust and confidence in DL models around users of these simulations, such as the farmer provided as an example.
Read the research in full
Multi-variable Hard Physical Constraints for Climate Model Downscaling
Jose González-Abad (Instituto de Física de Cantabria (IFCA), CSIC-UC)
Álex Hernández-García (Mila Quebec AI Institute and University of Montreal)
Paula Harder (Fraunhofer ITWM and University of Kaiserslautern)
David Rolnick (Mila Quebec AI Institute and McGill University)
José Manuel Gutiérrez (Instituto de Física de Cantabria (IFCA), CSIC-UC)
tags: AAAI, AAAI Fall Symposium 2023











