Theoretical remarks on feudal hierarchies and reinforcement learning

Reinforcement learning is a paradigm through which an agent interacts with its environment by trying out different actions at different states and observing the outcome. Each of these interactions can change the state of the environment, and can also provide rewards to the agent. The goal of the agent is to learn the value of performing each action on each state. By value, we mean the biggest amount of rewards that is possible for the agent to obtain after performing that action in that state. If the agent achieves this goal, it can then act optimally on its environment by choosing, at every state, the action that has the biggest value.

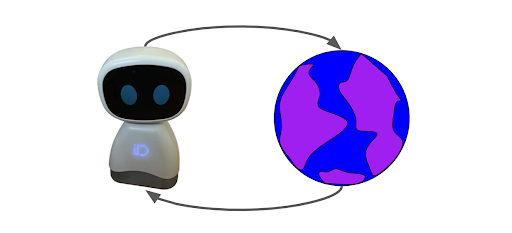In reinforcement learning, an agent interacts with its environment by making actions and observing their outcome, with the goal of selecting actions with the biggest value.

In 1989, Watkins proposed an algorithm to solve the reinforcement learning problem: Q-learning [1]. Not long after, the same Watkins and Dayan showed that the algorithm did indeed converge to the correct solution [2].

But we, humans, don’t just map states to the next best actions. If we want to get from where we are sitting right now to a friend’s house, we don’t just look at our environment, decide to stand up, then observe the environment again, decide to take a step forward, and so on and so forth. Before making each of these small decisions, we need to make bigger decisions. To achieve the goal of reaching our friend’s house, we need to define other goals that may include putting on our shoes, or getting on the bus down the street, and only then make small decisions that lead us to achieve them. We have a way of abstracting our decision making at different levels, in what resembles an hierarchy.

In 1992, Dayan himself and Hinton were thinking about this, and introduced the first idea for hierarchical reinforcement learning: feudal reinforcement learning [3]. In feudal reinforcement learning, the agent sets goals for an instance of itself and takes small steps to achieve them.

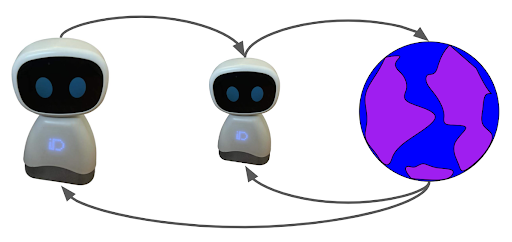
In hierarchical reinforcement learning, the agent sets goals to an instance of itself that interacts directly with the environment looking to achieve the goals set by the agent.

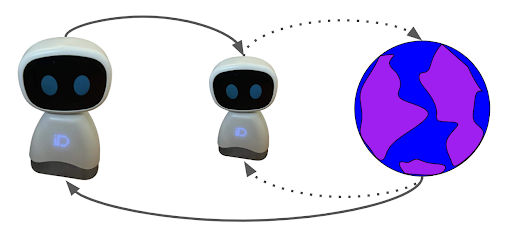
While learning occurs at different levels of the hierarchy at the same time, from the point of view of the agent, the environment is changing: as the instance of the agent becomes more competent in achieving the goals set, their outcomes also change. In our work, we show that, despite this fundamental difference, Q-learning also solves the hierarchical decision making process.

To establish our result, we first show that the dependencies within the hierarchy are smooth. Therefore, while the policy of the instance of the agent changes, the environment that the agent views also changes. Then, we show that Q-learning converges in changing, but converging, environments. Putting our two results together, we conclude that Q-learning converges with probability 1 to the correct solution at all levels of the hierarchy.

Hierarchies in reinforcement learning are not only human-inspired, but they also set the state of the art in complex decision making tasks, such as the game of Minecraft [5]. Furthermore, a well-constructed hierarchy allows for flexibility across different layers, as well as interpretability. With our results, we provided theoretical support for the use, and success, of hierarchies in reinforcement learning and motivated future research.

References

[1] Watkins, Christopher J. C. H. “Learning from delayed rewards”. PhD Thesis. 1989.
[2] Watkins, Christopher J. C. H. “Q-learning”. Machine Learning, 1992. 279-292.
[3] Dayan, Peter, Geoffrey Hinton. “Feudal reinforcement learning”. NeurIPS 1992. 279-292.
[4] Carvalho, Diogo S., Francisco S. Melo, Pedro A. Santos. “Theoretical remarks on feudal hierarchies and reinforcement learning”. ECAI 2023. IOS Press, 2023. 351-356.
[5] Lin, Zichuan, Junyou Li, Jianing Shi, Deheng Ye, Qiang Fu, Wei Yang. “Playing Minecraft with sample-efficient hierarchical reinforcement learning”. IJCAI 2022. 3257-3263.

This work won an outstanding paper award at ECAI 2023.

Diogo Carvalho is a PhD student at Instituto Superior Técnico of the University of Lisbon, and GAIPS of INESC-ID

Diogo Carvalho is a PhD student at Instituto Superior Técnico of the University of Lisbon, and GAIPS of INESC-ID