Crowdsourced clustering via active querying

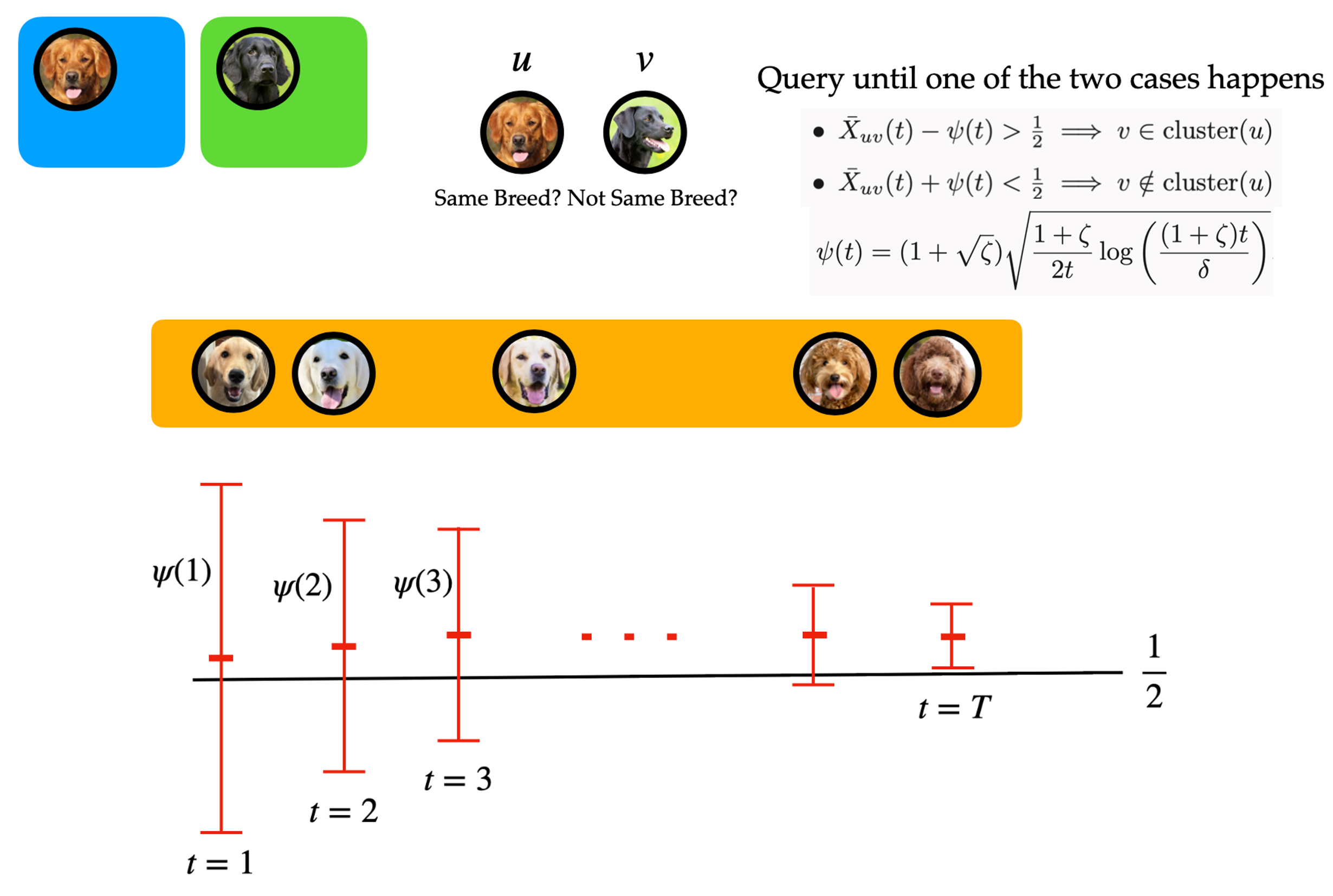Above: Illustration of our algorithm Active Crowdclustering. A pair is queried to different crowdworkers until the upper or the lower bound is below or above 1/2, respectively. The confidence bound is based on the law of the iterated logarithm. Below: Illustration of how the confidence interval changes as we obtain more queries. Eventually, the upper or the lower bound will cross 1/2.

The success of supervised learning relies on a good-quality labeled dataset. A prime example is ImageNet [1], which played an indispensable role in advancing object recognition; it contains millions of labeled images. Moreover, the internet is a huge repository of images and textual content that could potentially be leveraged for supervised learning. However, the sheer volume and diversity of this data present significant challenges, as it is impractical for researchers themselves to label these data manually.

Consider building a vision system that can identify various dog breeds. Let us say we have obtained images of dogs of various breeds. To label the breed of each dog, we could hire an expert. However, experts are rare, costly, and challenging to train. An alternative way is to hire crowdworkers. However, due to their lack of expertise, asking them to directly label the breed is not ideal. Instead, we could ask them to compare the similarity between two images of dogs. Such a comparison task is much easier since it does not require expertise:

Do dog image and image belong to the same breed?

By treating these dog images as nodes and using the comparison query’s answer to indicate whether there is an edge between two images, we can construct a graph. We could apply graph clustering algorithms on the graph to obtain the clustering and label at cluster level.

Naturally, one would ask which pairs of images should we query to the crowds. A type of approach involves querying a random subset of all possible pairs before running a graph clustering algorithm. This type of method is known as the passive method. The drawback of these approaches is that they can only recover clusters of size , which is related to the hidden clique conjecture.

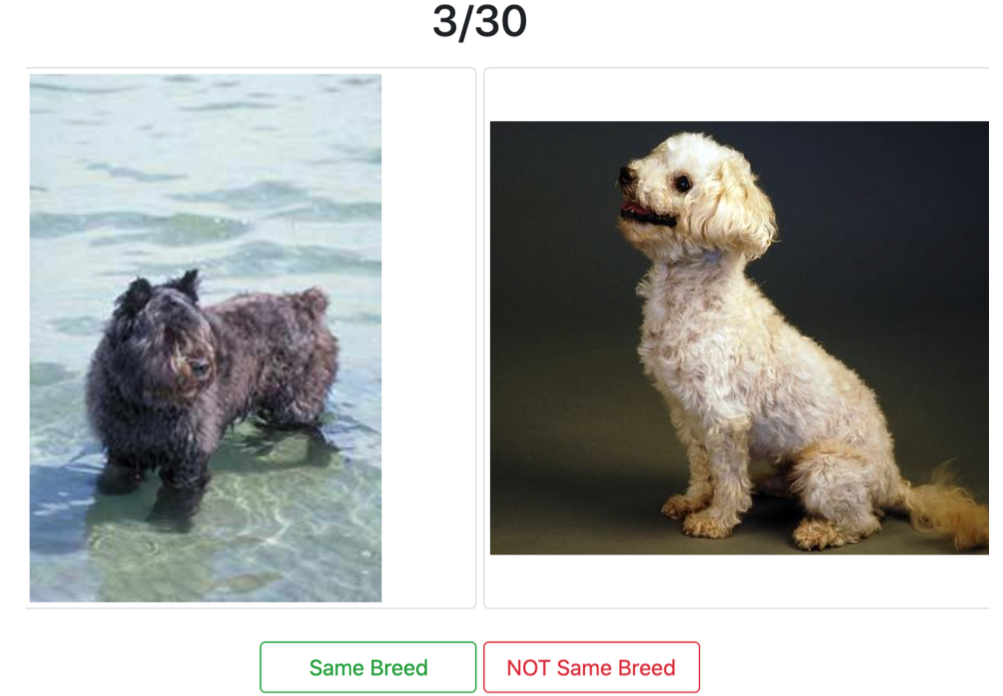Figure 1: A sample of our pairwise queries interface displayed to the crowdworkers on Amazon Mechanical Turk.

To address this issue, many methods [2][3] have tried to actively select which images to be queried. However, they typically come with severe limitations, such as they need to know the number of clusters a priori, or they assume that crowdworkers’ error is parametrized by a single scaler. These limitations make these methods impractical.

Therefore, we propose Active Crowdclustering, which does not rely on any unknown parameters and can recover clusters regardless of their sizes. Moreover, it is computationally efficient and simple to implement. Lastly, we provide a theoretical guarantee, under mild assumptions that crowdworkers are independent and better than random guessers, that we can recover exactly the clusters with high probability.

Our algorithm works as follows:

1. A randomly chosen item forms the first singleton cluster.
2. Query a non-clustered item with each representative item of the existing clusters.
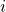3. To decide if belongs to the cluster that contains 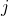, we repeatedly query different crowdworkers until the membership of 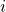can be established with confidence, which is based on the law of the iterated logarithm (LIL) [4, 5, 6].
4. Item 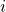forms a new cluster itself if it is determined not to belong to any of the existing clusters.

It’s important to reiterate that our algorithm does not require prior knowledge of the problem parameters, as we do not predetermine the number of times to repeat the query. Instead, we use LIL-based time varying confidence intervals and decide when to stop on the fly.

We conducted real world experiments on Amazon Mechanical Turk using the Dogs3 (3 large clusters ) and Birds20 (20 small clusters ) dataset. Figures 2 and 3 illustrate the clustering outcome. Experiments on Birds20 show that our Active Crowdclustering succeeds regardless of cluster sizes, in stark contrast to the notable failures of passive methods. Moreover, although passive methods give good clustering outcomes on Dogs3 (large clusters) our method can pick up more granular differences within each ground-truth cluster.

Figure 2: Clusters obtained by our method on the Dogs3 dataset. More granular clusters are obtained, e.g., differently groomed Poodles formed their own cluster, images of Norfolk Terriers that look different from the large subset of Norfolk Terriers form their own clusters.

Figure 3: Clusters obtained by our method on the Birds20 dataset. In this small cluster regime, our active method provides much better clustering outcomes than passive clustering.

In summary, we propose a practical active clustering algorithm which

1. does not require the knowledge of problem parameters;
2. can recover clusters regardless of their sizes;
3. can pick up more granular differences;
4. has theoretical guarantee under mild assumptions.

For more details, please read our full paper, Crowdsourced Clustering via Active Querying: Practical Algorithm with Theoretical Guarantees, from HCOMP 2023.

References

[1] Olga Russakovsky*, Jia Deng*, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg and Li Fei-Fei (* = equal contribution), ImageNet Large Scale Visual Recognition Challenge. IJCV, 2015.
[2] Yun, Se-Young and Proutiere, Alexandre, Community detection via random and adaptive sampling. Conference on learning theory, pp. 138–175,(2014), PMLR.
[3] Mazumdar, Arya and Saha, Barna, Clustering with noisy queries. Advances in Neural Information Processing Systems 30 (2017), NeurIPS.
[4] Khintchine, Aleksandr, Über einen Satz der Wahrscheinlichkeitsrechnung. Fundamenta Mathematicae 6.1 (1924): 9-20.
[5] Kolmogoroff, A., Über das Gesetz des iterierten Logarithmus. Mathematische Annalen 101 (1929): 126-135.
[6] Jamieson, Kevin, et al., lil’ucb: An optimal exploration algorithm for multi-armed bandits. Conference on Learning Theory (2014), PMLR.

Funding Acknowledgement

This work was partially supported by NSF grants NCS-FO 2219903 and NSF CAREER Award CCF 2238876.

Yi Chen is a Ph.D. student at the University of Wisconsin-Madison.

Yi Chen is a Ph.D. student at the University of Wisconsin-Madison.

Ramya Korlakai Vinayak is an assistant professor at the University of Wisconsin-Madison

Ramya Korlakai Vinayak is an assistant professor at the University of Wisconsin-Madison

Babak Hassibi is the Mose and Lilian S. Bohn Professor of Electrical Engineering at the California Institute of Technology

Babak Hassibi is the Mose and Lilian S. Bohn Professor of Electrical Engineering at the California Institute of Technology