
ΑΙhub.org
The moderating effect of instant runoff voting
Elections are the core tool of democracy, where we seek to combine the preferences of a society into a single collective decision: electing a president, deciding between policy proposals, or even picking Academy Award winners. But aggregating preferences turns out to be a very tricky business; hundreds of years of research dating back to the Marquis de Condorcet (1743-1794) has established that no perfect voting system is possible. For instance, Condorcet himself showed that groups can have cycles in their preferences, preferring A to B, B to C, and C to A. In such a setting, how can we possibly pick a winner? Due to this inherent paradox – and the famous impossibility results of Arrow, Gibbard, and Satterthwaite – all voting systems are less-than-ideal compromises (some less ideal than others).
Most single-winner elections worldwide use plurality voting: everyone is asked to pick their favorite, and the candidate with the most votes wins. Despite its alluring simplicity, plurality has a host of shortcomings, including susceptibility to vote-splitting among similar candidates and strong incentives to vote for candidates other than the most preferred one. In fact, a poll of election experts ranked plurality worst among nine proposed voting systems; a particular concern is how plurality behaves in polarized societies, often failing to elect a good compromise.
One increasingly-popular contender to dethrone plurality, particularly in the United States, is instant runoff voting (IRV; also known as ranked-choice voting and the alternative vote, among other names). Under IRV, everyone ranks the candidates rather than providing only their top choice. We then repeatedly eliminate the candidate with the fewest first-place votes, reallocating votes to the next-preferred candidate on each ballot. The last candidate remaining wins (alternatively, you can stop when one candidate reaches a majority, since they are then guaranteed to be the last remaining). In effect, IRV runs multiple rounds of run-off elections instantly, without the need for voters to return to the polls – hence the name.
There has been a heated debate around the adoption of IRV over plurality, with some arguing that it would help address partisan divides and others claiming it would amplify them. In our recent AAAI 2024 paper “The Moderating Effect of Instant Runoff Voting,” my coauthors Johan Ugander, Jon Kleinberg, and I provide a mathematical backing for the argument that IRV favors moderate candidates in a way that plurality doesn’t. It’s well known that all voting systems satisfying the Condorcet criterion (if a candidate would win any pairwise election, then a voting system should pick them) have a strong moderating effect: they elect the candidate most preferred by the median voter. However, neither plurality nor IRV satisfy the Condorcet criterion, requiring us to develop new tools to analyze them.
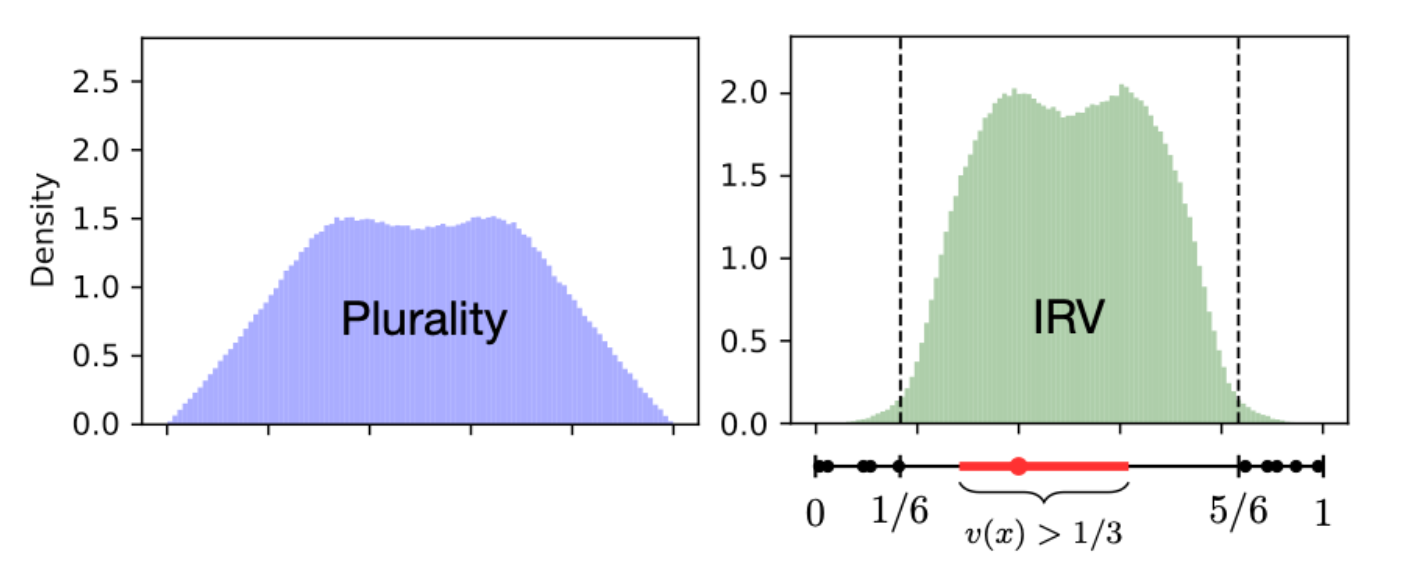
We relax the Condorcet-based notion of a moderating effect (always electing the median voter’s favorite) to allow a wider range of policies around the center (always electing a candidate within some distance of the median voter). What exactly this range is depends on the distribution of voters: for instance, with voters distributed uniformly, we say that a candidate in the middle two-thirds of the political spectrum is moderate. Given this looser notion of a moderate, our main proof that IRV has a moderating effect is simple in structure (see the diagram below):
- Under IRV, candidates are eliminated one at a time, so at some point, only one moderate candidate remains (assuming at least one moderate ran for election).
- The remaining extreme candidates are then too far away from the last moderate to “squeeze them out,” leaving the moderate with more votes than some extremist, who is eliminated next.
- Eventually, all the extreme candidates are eliminated, and the last moderate wins.

There are a number of technical assumptions we invoke to make this outline mathematically rigorous; for instance, we assume the ideological spectrum is one-dimensional (e.g., from the far left to the far right) and that voters rank candidates by ideological distance. We also assume that voters are symmetrically distributed. Our argument is simplest for uniformly-distributed voters, but we show the same idea applies to other symmetric voter distributions. Finally, if voters are extremely polarized (when most of them are near the boundaries of the ideological space), then IRV can no longer elect moderates. (The relevant notion of extreme polarization is genuinely extreme; modern democracies likely do not fall into this regime. For instance, despite widespread concern about polarization, more than 1/3 of Americans identify as moderate.)
In contrast, we prove that arbitrarily extreme candidates can win plurality elections, regardless of how voters are distributed. It’s even possible for 99% of voters to be on the far left and for plurality to elect a far-right candidate (if the field of candidates on the left is sufficiently crowded). One of our results that is particularly nice from a mathematical angle is that the distribution of plurality winners with uniformly distributed voters and candidates converges to uniform as the number of candidates grows (meanwhile, this is very much not the case for IRV, which as we saw only elects moderates). This proof relies on a connection to the statistical theory of stick-breaking processes.
In short, we show that IRV favors moderates in a way plurality doesn’t, despite neither satisfying the Condorcet criterion. This moderating effect persists even with polarized voters (although only up to a point). We hope that these results will provide meaningful context in the ongoing debate between plurality and IRV, and that our methods – which enabled our surprising and often simple results – can be useful in the study of electoral systems.
Funding statement
This research was supported in part by ARO MURI, a Simons Investigator Award, a Simons Collaboration grant, a grant from the MacArthur Foundation, the Koret Foundation, and NSF CAREER Award #2143176.
tags: AAAI, AAAI2024











