
ΑΙhub.org
Proportional aggregation of preferences for sequential decision making
Problem statement
In various decision making settings, from recommendation systems to hiring processes, often a sequence of decisions are made by a group. A naive approach to decision-making in such scenarios is to select the alternative with the highest supporters in each round. However, this method can lead to unrepresentative outcomes, where a majority dictates all decisions, potentially disincentivizing participation from minority groups.
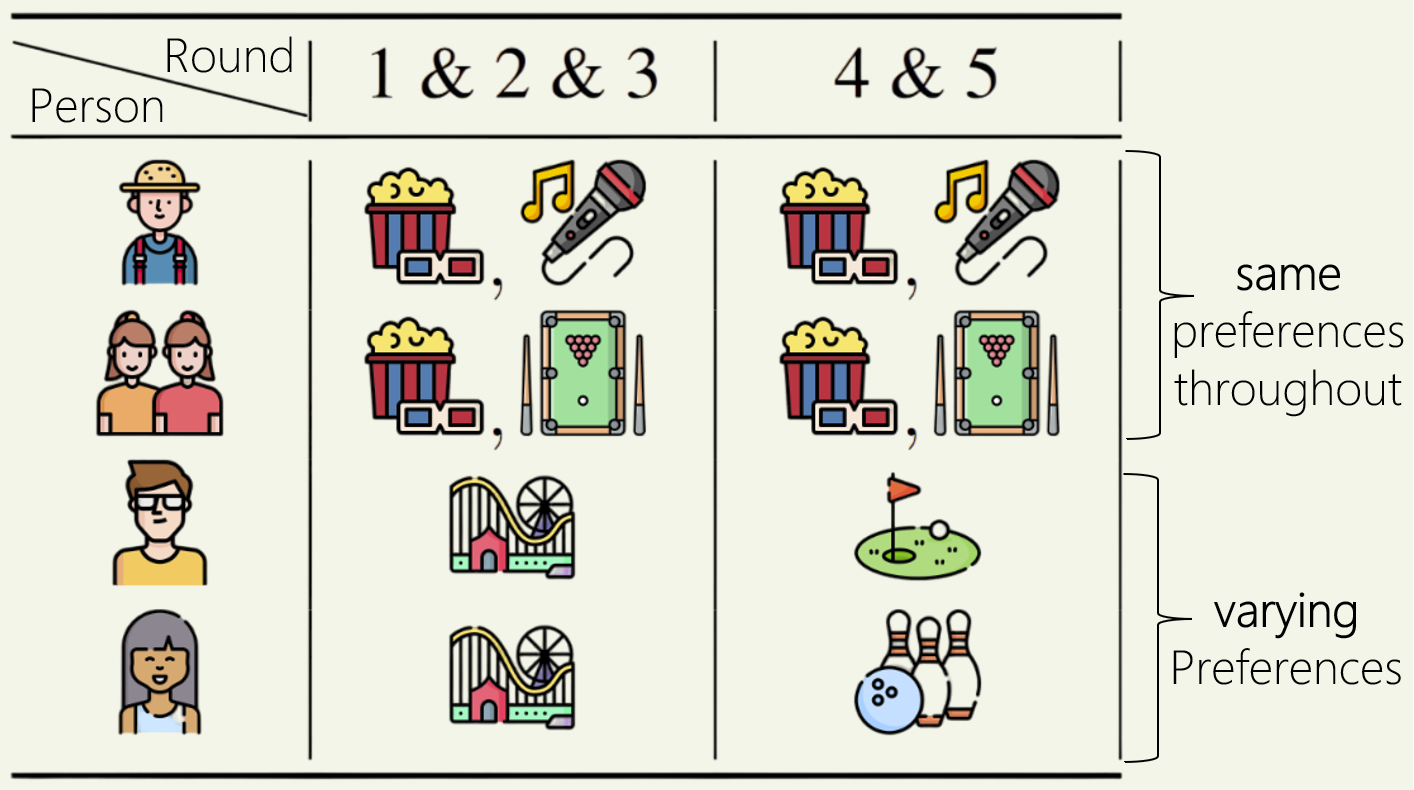
Consider the following example where a group of ![]() friends (voters) want to hang out together weekly. They have diverse choices for the activities (alternatives) they approve of every week (round), but only one activity can be chosen as the decision (i.e., the activity which the whole group ends up pursuing even if some don’t like it).
friends (voters) want to hang out together weekly. They have diverse choices for the activities (alternatives) they approve of every week (round), but only one activity can be chosen as the decision (i.e., the activity which the whole group ends up pursuing even if some don’t like it).
In the example above, there is a group of five people and for each person, the activities they approve in each round is shown (for example, person 4, a young man with specs, prefers going out only to amusement park in the first 3 rounds and then for golf in the last two rounds). Overall, movies is the majority choice in every round, as it is always supported by persons 1-3, which is ![]() of the group. However, going with the majority choice in each round would leave persons 4,5 unsatisfied throughout!
of the group. However, going with the majority choice in each round would leave persons 4,5 unsatisfied throughout!
Can we do something more equitable such that every member’s preferences are represented fairly? This paper addresses this challenge for general sequential decision making problems given approval votes through the lens of Social Choice Theory.
Applications
Let’s first discuss some applications where this problem surfaces, with examples.
- Hiring Processes (University): New faculty constantly need to be hired for a department. Existing faculty members want to recruit people they can collaborate with. How to ensure that over a series of hiring rounds, the entire department’s spectrum of research interests is represented?
- Virtual Democracy: When making similar decisions repeatedly, we can use ML to build models of user preferences, which can be used on their behalf when the preference elicitation costs are high and outweigh the impact of each individual decision. Eg: AI systems forced to make ethical decisions quickly and repeatedly, such as autonomous vehicles in moral dilemmas like the trolley problem. In such a case, we would like people’s preferences to be reflected fairly.
- Uncertainty about the goal: Suppose we are managing an intelligent system (like a robot) that repeatedly decides on an action in order to maximize an objective function we specify. But we may not be certain about our desired objective function (for example, because we have moral uncertainty). In such a case, we can decide on a mixture of objectives (20% on objective 1, etc.). Over a sequence of decisions, we would like the system to ensure that each objective is satisfied at least to an extent proportional to its importance/weight.
Main idea: Proportionality axioms
The core fairness concept we study is that of proportionality. Hypothetically, suppose a group is making decisions over 10 rounds and 30% of the group always has movie as their preferred alternative while the remaining 70% always want golf, then 3 out of 10 decisions should be movie and rest 7 out of 10 should be golf. While for a single decision, the best thing to do might be going with the majority, over multiple rounds we can hope to satisfy different groups in each round to achieve more equitable outcomes.
However, a challenge is that there are not always well-demarcated ‘groups’ in the real-world. Further, the set of alternatives might change in each round, leading to the formation of completely new groups every time. Sometimes voters that agree once can also disagree on later rounds. How do we cleanly incorporate such variations?
We say a “group” (of voters) agrees in a round if 1 or more alternatives are approved by all of them.
We propose proportionality guarantees of the following form: Every group ![]() of
of ![]() % voters that agrees in
% voters that agrees in ![]() of the rounds, must approve
of the rounds, must approve ![]() % of the decisions:
% of the decisions:

But what does it mean for a group to approve ![]() % of decisions?
% of decisions?
We can’t have all members of the group approving ![]() % of the decisions. Prior work has shown that this property can’t be satisfied in even simpler settings like apportionment (where the alternatives and approval profile of every voter are same in each round) — (Example 1).
% of the decisions. Prior work has shown that this property can’t be satisfied in even simpler settings like apportionment (where the alternatives and approval profile of every voter are same in each round) — (Example 1).
So we study two types of (weaker) guarantees based on individual members of ![]() that can actually be satisfied (as we will show later).
that can actually be satisfied (as we will show later).
Strong Proportional Justified Representation (Strong-PJR): There are at least ![]() % rounds where any member of
% rounds where any member of ![]() approves the decision of that round.
approves the decision of that round.
Strong Extended Justified Representation (Strong-EJR): There is at least one consistent member of ![]() that approves the decision of
that approves the decision of ![]() % rounds.
% rounds.
If ![]() satisfies Strong-EJR, then the
satisfies Strong-EJR, then the ![]() % rounds where the lucky member of
% rounds where the lucky member of ![]() approves decisions help satisfy Strong-PJR. Thus, satisfying Strong-EJR implies satisfying Strong-PJR.
approves decisions help satisfy Strong-PJR. Thus, satisfying Strong-EJR implies satisfying Strong-PJR.
Let’s understand these axioms with the friends outings example presented earlier.

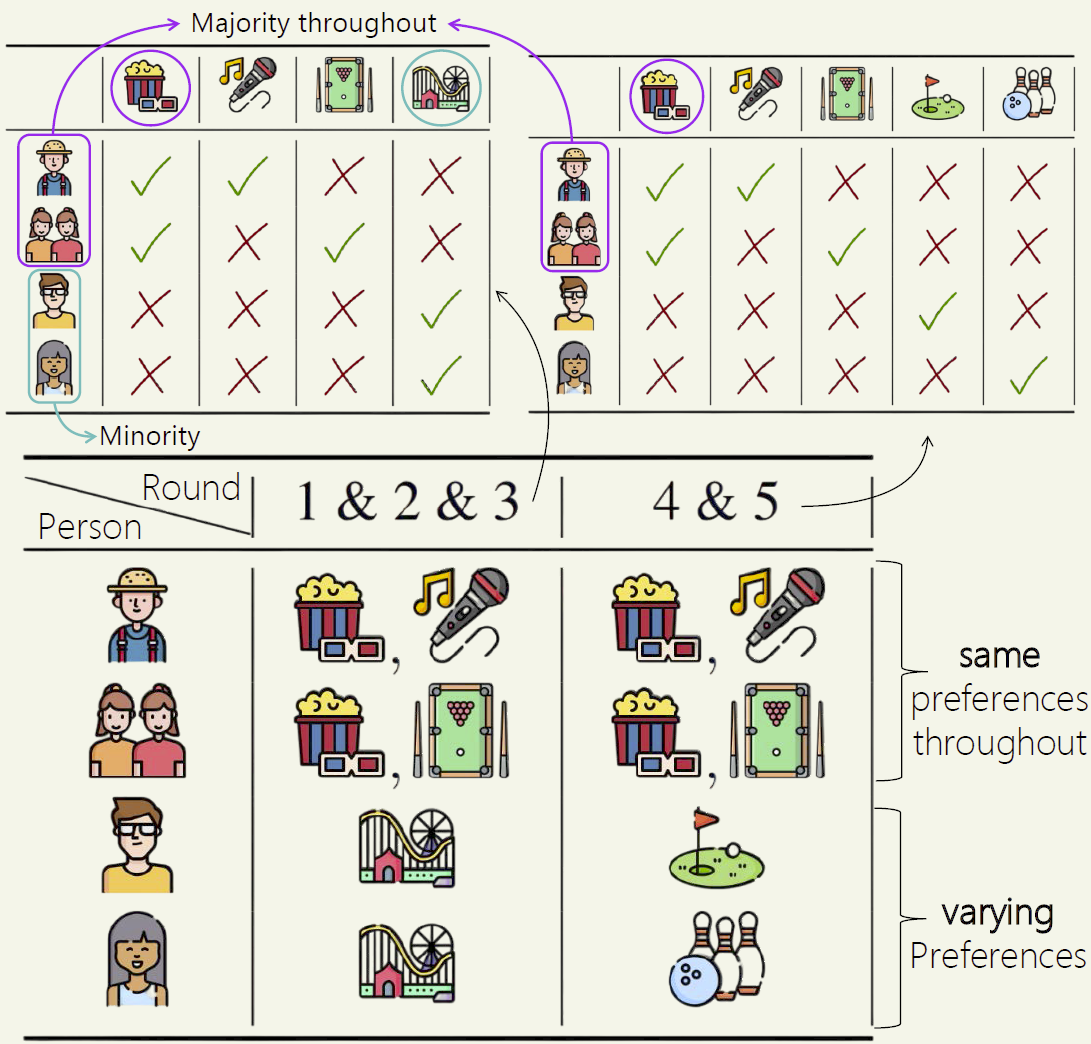
Let Group A be persons 1-3 (the group depicted with same preferences in the picture above), and Group B be persons 4-5 (rest of the people — depicted with varying preferences) from the example above. First, how many decisions do these groups deserve?
Group A is 60% of voters, and they agree in every round through the movie alternative. Thus, they deserve to approve decisions of ![]() %
% ![]() rounds. Group B is 40% of voters, and they only agree in rounds 1-3 thorough the amusement park alternative. Thus, they deserve to approve decisions of
rounds. Group B is 40% of voters, and they only agree in rounds 1-3 thorough the amusement park alternative. Thus, they deserve to approve decisions of ![]() %
% ![]() rounds.
rounds.
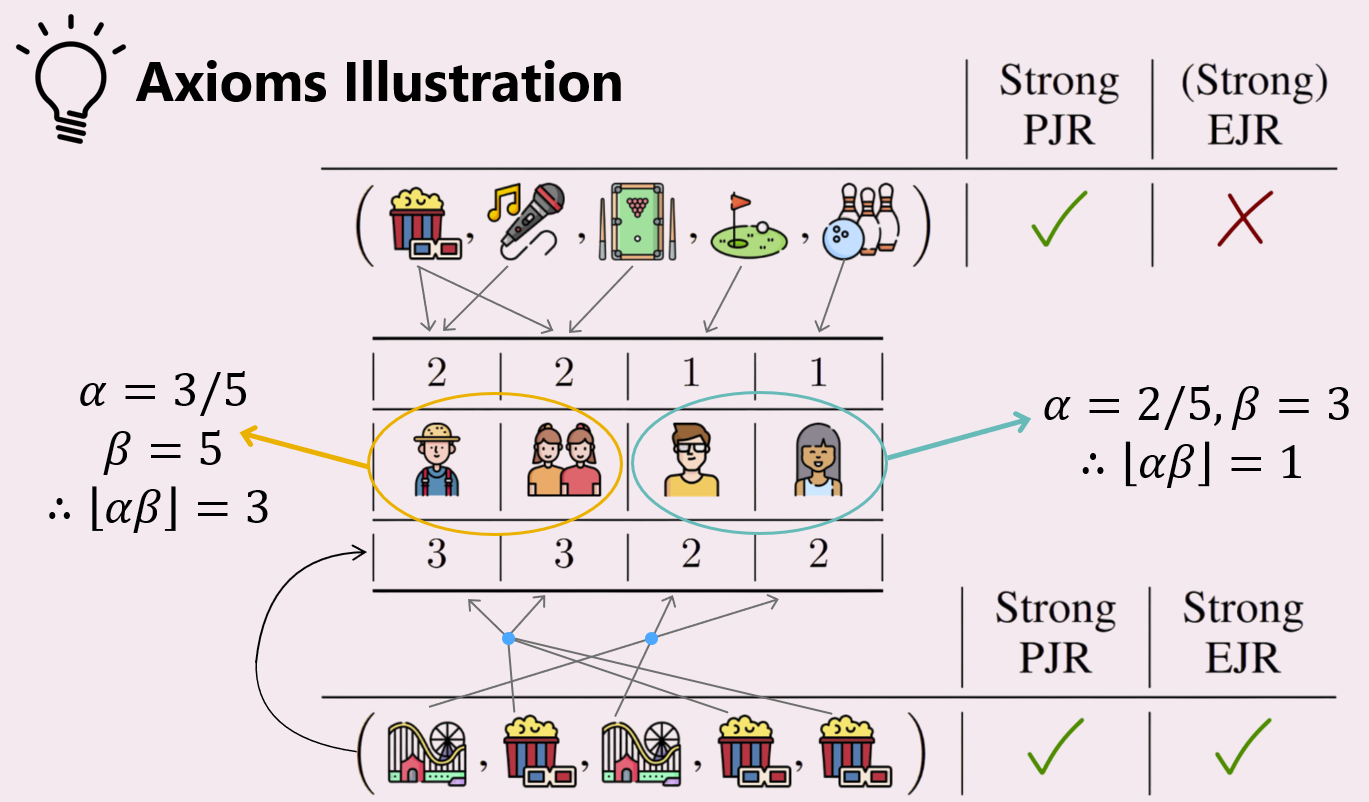
Now lets consider the decision sequence on the top (of the above image), i.e. (movie, karaoke, pool, golf, bowling). Person 1 approves 2 decisions (round 1, 2), persons 2-3 approve 2 decisions (round 1, 3), and persons 4, 5 each approve 1 decision (rounds 4, 5 respectively).
For Strong-PJR, we need 3 rounds such that any member of Group A approves the decision in those 3 rounds, and similarly 2 such rounds for Group B. We achieve this through rounds 1-3 for Group A, and rounds 4-5 for Group B. Thus, this sequence of decisions satisfies Strong-PJR.
However, for Strong-EJR, we need one specific member in Group A to approve 3 decisions, and one specific member in Group B to approve 2 decisions. However, the maximum satisfaction (number of decisions approved) for any member in Group A is 2, and for Group B members is 1. Thus, this decision sequence fails Strong-EJR.
Exercise for the reader: Verify that the decision sequence on the bottom, i.e. (amusement park, movie, amusement park, movie, movie) satisfies both Strong-PJR and Strong-EJR.
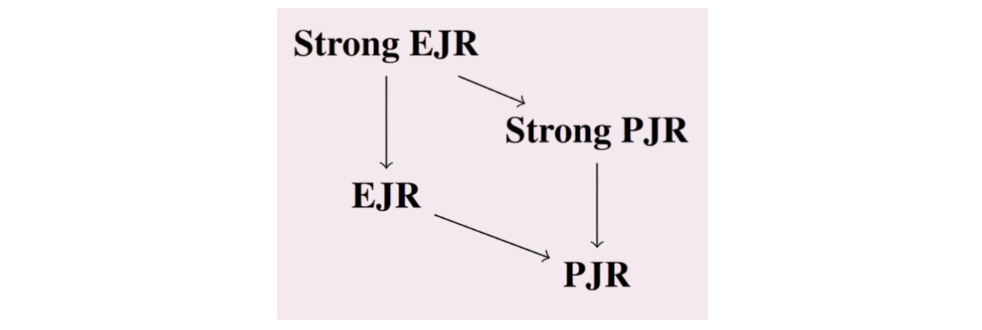
You might be wondering why we call these axioms ‘Strong’ PJR and EJR. Is there a ‘weak’ version? Well, there’s a not-’Strong’ version, when we only consider groups that agree on all rounds, i.e. ![]() , a decision sequence can satisfy PJR if
, a decision sequence can satisfy PJR if ![]() % of all the decisions are approved by some member of the group, or EJR if some member in the group approves
% of all the decisions are approved by some member of the group, or EJR if some member in the group approves ![]() % decisions. The following figure shows the implication graph for each axiom. Thus, the not-’Strong’ variant has more stringent criteria on what qualifies as a group by requiring members to agree on all rounds.
% decisions. The following figure shows the implication graph for each axiom. Thus, the not-’Strong’ variant has more stringent criteria on what qualifies as a group by requiring members to agree on all rounds.
Well, that’s about specific decision sequences. How do these properties help us analyze algorithms (voting rules) to make these decisions? We say an algorithm satisfies (Strong) PJR/EJR if for every possible “voting profile” (a sequence of rounds, with varying alternatives and arbitrary voter approvals in each round), the decision sequence produced by the algorithm satisfies that property. As you might notice, this is a worst-case guarantee — if the algorithm’s outcome fails to satisfy the property on even one input instance, we say the algorithm doesn’t satisfy the property.
Theoretical results
Tightness of axioms: You might also be wondering why stop at ![]() % decisions being approved, and not try for more. We show, in the paper, that if we make the requirement
% decisions being approved, and not try for more. We show, in the paper, that if we make the requirement ![]() %
% ![]() decisions, for any
decisions, for any ![]() , there are input instances where no decision sequence would satisfy these axioms. Further, even if we only consider instances where such a decision sequence exists, no online decision making algorithm can always find it.
, there are input instances where no decision sequence would satisfy these axioms. Further, even if we only consider instances where such a decision sequence exists, no online decision making algorithm can always find it.
Wait, what exactly is an ‘online’ algorithm in this context?
We actually consider three different settings for algorithms:
- Online: The algorithm only knows information about previous rounds, and the voter profile of the current round. It has no knowledge about the subsequent (future) rounds.
- Offline: The algorithm knows voter profiles about all rounds from the beginning.
- Semi-online: The algorithm doesn’t have any information about subsequent rounds, but knows the total number of rounds in advance.
We consider popular algorithms in multiwinner voting literature for each of these settings, namely, Phragmen’s Sequential method for the online setting, Proportional Approval Voting (PAV) for the offline setting, and the Method of Equal Shares (MES) for the semi-online setting. Our theoretical results are summarized below, and you can check the paper out for proofs.

In the offline setting, we find PAV, and even an approximate variant of it that runs in polynomial time, can satisfy all our properties. This is promising!
However, in the online setting, we show that any algorithm satisfying (Strong) EJR would resolve a popular open problem in multiwinner voting, satisfying something called “committee monotonicity” and EJR simultaneously. Sequential Phragmen is good enough to satisfy the Strong-PJR rule.
Finally, the Method of Equal Shares gives an interesting result. It satisfies EJR (not Strong EJR), but fails at Strong PJR, showing how it can sometimes be harder to provide justified representation to groups that don’t agree in all rounds. It remains an open-question to find an algorithm that satisfies both EJR and Strong PJR in a semi-online setting. Finding a semi-online rule satisfying Strong EJR would also solve this by implication.
Experiments
We empirically compared the fairness and utility outcomes of the voting algorithms we studied (Phragmen, MES, PAV) to some methods proposed in prior work. We used both synthetically generated voting profiles, and also real-world data from California elections. These results can be found in our paper. Here, we will focus on what we think was the more interesting experiment on the
Goal
We wish to see if proportional aggregation of (individual) learnt models of each user’s preferences can lead to more fair outcomes than the traditional approach of learning a single combined model across users.
Setup
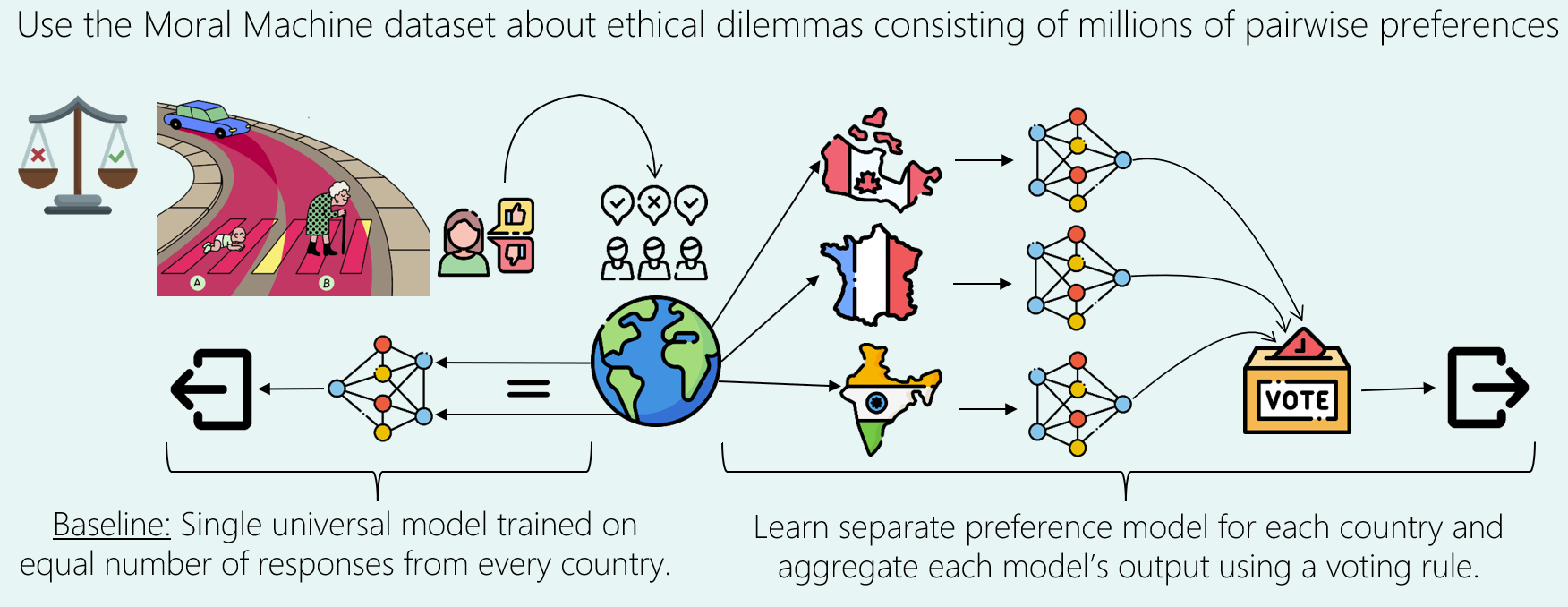
Since there was a paucity of samples per individual (only 14 on an average), so we decided to club all users from a single country as 1 voter, which gave us an average of ~200 pairwise preferences to learn a model from.
The baseline approach involves training a single universal model on an equal number of responses from every country. This model represents a traditional method where all data (equal number of responses from every category) is combined to form a general preference model.
Our proposed method involves training separate preference models for each country, containing all pairwise comparisons provided by respondents from that country. The outputs of these models are then aggregated using voting rules (discussed above) to make sequences of decisions.
Results
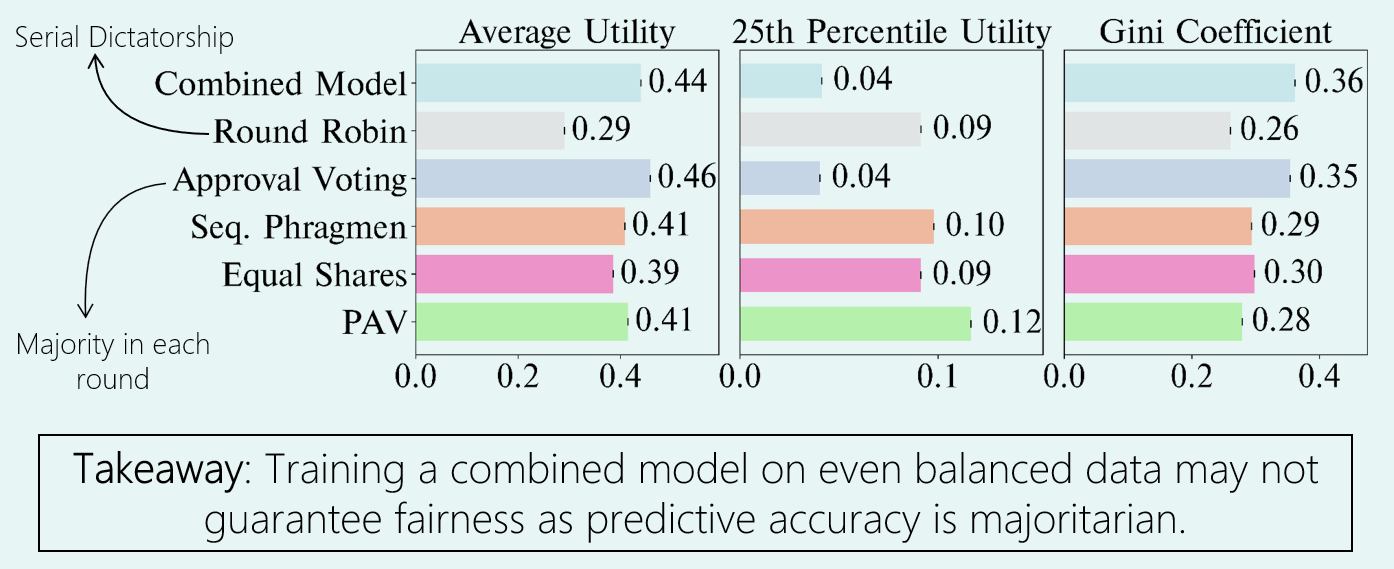
As you can see in the graphs above, the Combined Model behaves similarly to the Approval Voting method, which picks the alternative with most votes in each round. This means, the traditional learning paradigm of learning a single combined model that maximizes predictive accuracy turns out to be very similar to majoritarian. Compared to learning voter-specific models and using proportional aggregation algorithms, combined models have worse fairness as shown by higher Gini coefficient (a measure of inequality), at only slightly better average utility. You can check out our paper for more setup details and variations.
Conclusion
Our work addresses the challenge of ensuring fairness in sequential decision making. By leveraging proportionality concepts from Social Choice Theory, we provide both theoretical foundations and practical methods to guarantee that the preferences of all participants are fairly represented when making a sequence of decisions. The applications could vary from something as naive as where to go out with your friends, to making AI systems better represent preferences of all sections of society. We hope to see these insights applied to preference alignment in today’s large-scale AI systems, especially when they are being deployed as part of critical decision-making systems.
Nikhil Chandak, Shashwat Goel and Dominik Peters won an outstanding paper award at AAAI 2024 for the work summarized in this blog post. You can read the full paper (“Proportional Aggregation of Preferences for Sequential Decision Making”) here.
tags: AAAI, AAAI2024, deep dive












