
ΑΙhub.org
Learning robust controllers that work across many partially observable environments
In intelligent systems, applications range from autonomous robotics to predictive maintenance problems. To control these systems, the essential aspects are captured with a model. When we design controllers for these models, we almost always face the same challenge: uncertainty. We’re rarely able to see the whole picture. Sensors are noisy, models of the system are imperfect; the world never behaves exactly as expected.
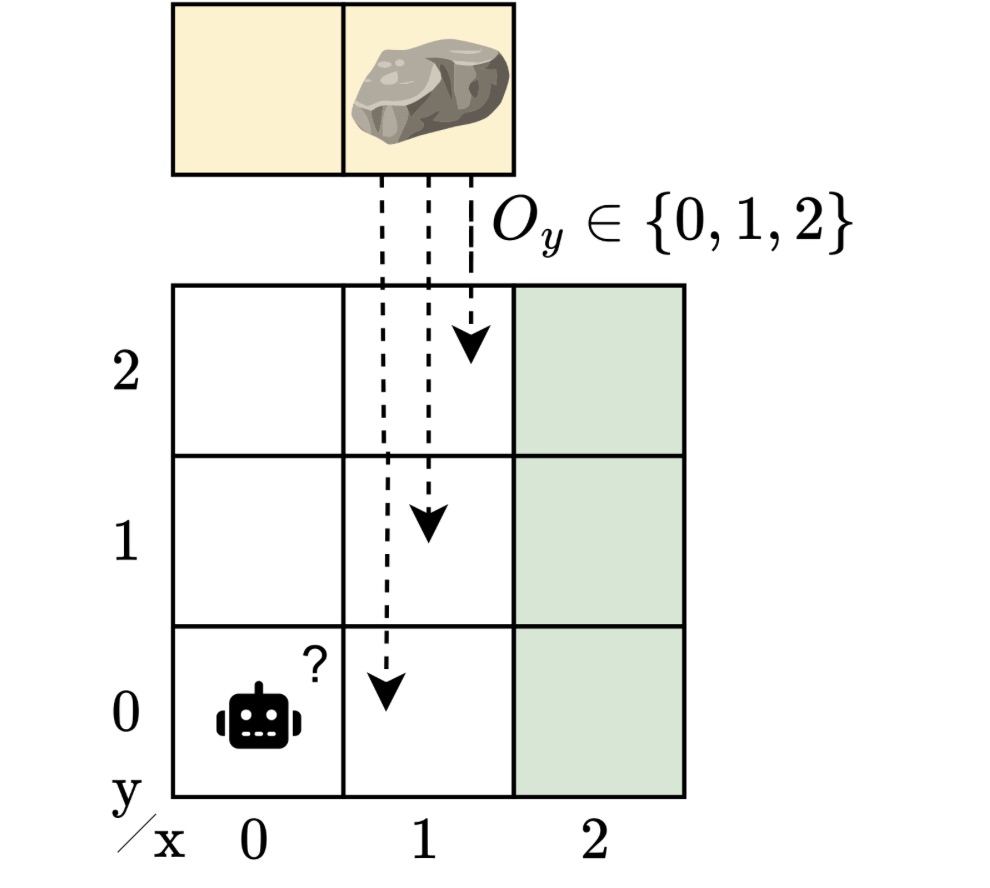
Imagine a robot navigating around an obstacle to reach a “goal” location. We abstract this scenario into a grid-like environment. A rock may block the path, but the robot doesn’t know exactly where the rock is. If it did, the problem would be reasonably easy: plan a route around it. But with uncertainty about the obstacle’s position, the robot must learn to operate safely and efficiently no matter where the rock turns out to be.
This simple story captures a much broader challenge: designing controllers that can cope with both partial observability and model uncertainty. In this blog post, I will guide you through our IJCAI 2025 paper, “Robust Finite-Memory Policy Gradients for Hidden-Model POMDPs“, where we explore designing controllers that perform reliably even when the environment may not be precisely known.
When you can’t see everything
When an agent doesn’t fully observe the state, we describe its sequential decision-making problem using a partially observable Markov decision process (POMDP). POMDPs model situations in which an agent must act, based on its policy, without full knowledge of the underlying state of the system. Instead, it receives observations that provide limited information about the underlying state. To handle that ambiguity and make better decisions, the agent needs some form of memory in its policy to remember what it has seen before. We typically represent such memory using finite-state controllers (FSCs). In contrast to neural networks, these are practical and efficient policy representations that encode internal memory states that the agent updates as it acts and observes.
From partial observability to hidden models
Many situations rarely fit a single model of the system. POMDPs capture uncertainty in observations and in the outcomes of actions, but not in the model itself. Despite their generality, POMDPs can’t capture sets of partially observable environments. In reality, there may be many plausible variations, as there are always unknowns — different obstacle positions, slightly different dynamics, or varying sensor noise. A controller for a POMDP does not generalize to perturbations of the model. In our example, the rock’s location is unknown, but we still want a controller that works across all possible locations. This is a more realistic, but also a more challenging scenario.
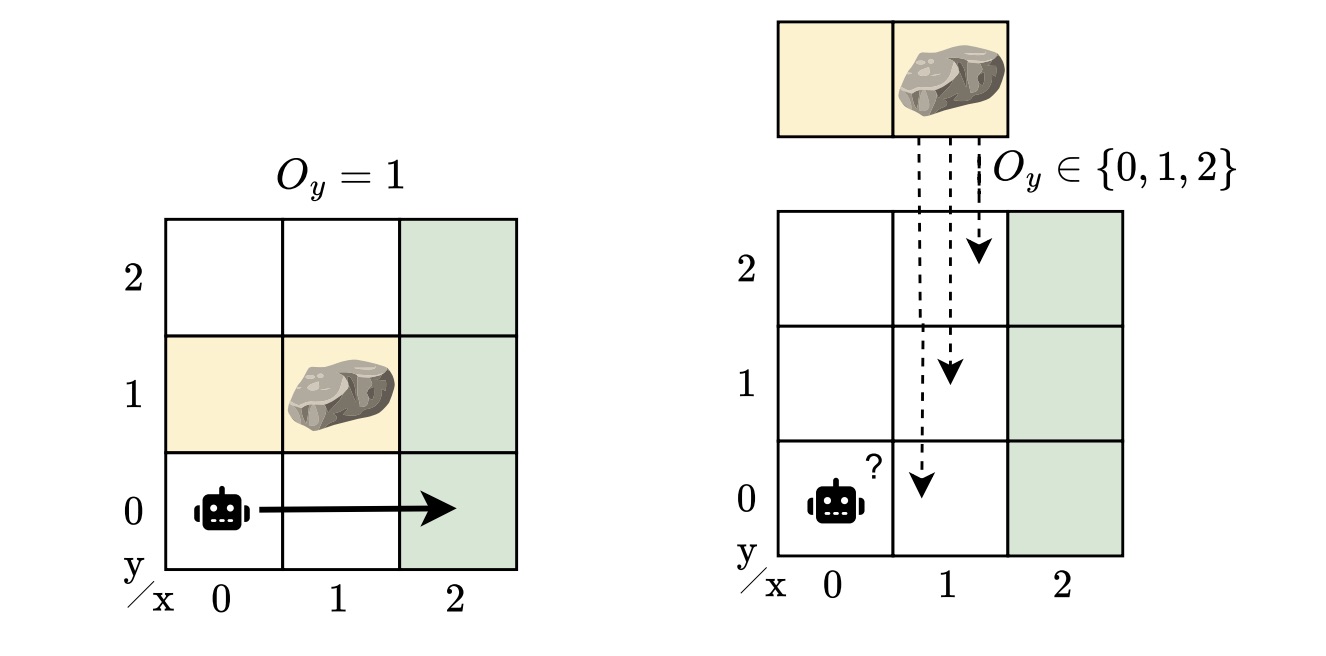
To capture this model uncertainty, we introduced the hidden-model POMDP (HM-POMDP). Rather than describing a single environment, an HM-POMDP represents a set of possible POMDPs that share the same structure but differ in their dynamics or rewards. An important fact is that a controller for one model is also applicable to the other models in the set.
The true environment in which the agent will ultimately operate is “hidden” in this set. This means the agent must learn a controller that performs well across all possible environments. The challenge is that the agent doesn’t just have to reason about what it can’t see but also about which environment it’s operating in.
A controller for an HM-POMDP must be robust: it should perform well across all possible environments. We measure the robustness of a controller by its robust performance: the worst-case performance over all models, providing a guaranteed lower bound on the agent’s performance in the true model. If a controller performs well even in the worst case, we can be confident it will perform acceptably on any model of the set when deployed.
Towards learning robust controllers
So, how do we design such controllers?
We developed the robust finite-memory policy gradient rfPG algorithm, an iterative approach that alternates between the following two key steps:
- Robust policy evaluation: Find the worst case. Determine the environment in the set where the current controller performs the worst.
- Policy optimization: Improve the controller for the worst case. Adjust the controller’s parameters with gradients from the current worst-case environment to improve robust performance.
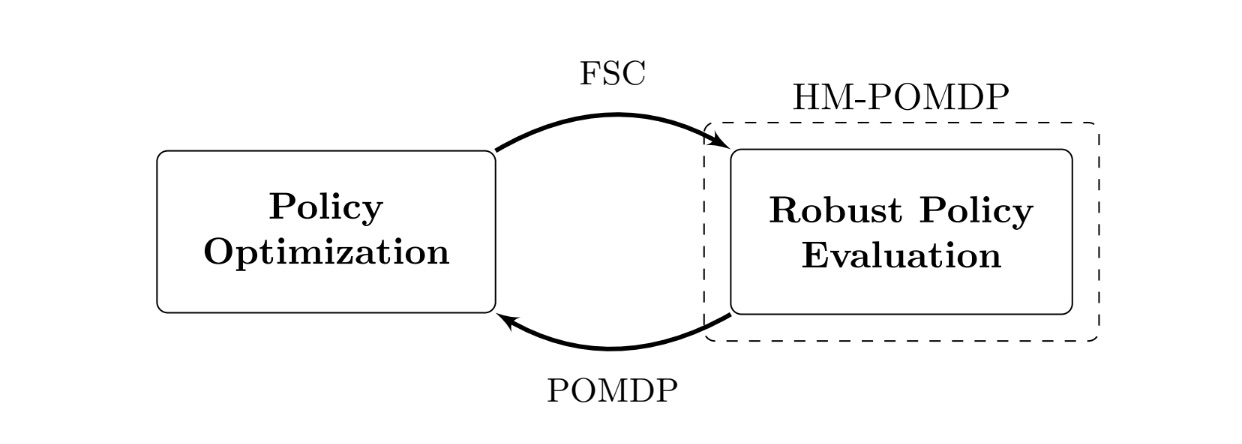
Over time, the controller learns robust behavior: what to remember and how to act across the encountered environments. The iterative nature of this approach is rooted in the mathematical framework of “subgradients”. We apply these gradient-based updates, also used in reinforcement learning, to improve the controller’s robust performance. While the details are technical, the intuition is simple: iteratively optimizing the controller for the worst-case models improves its robust performance across all the environments.
Under the hood, rfPG uses formal verification techniques implemented in the tool PAYNT, exploiting structural similarities to represent large sets of models and evaluate controllers across them. Thanks to these developments, our approach scales to HM-POMDPs with many environments. In practice, this means we can reason over more than a hundred thousand models.
What is the impact?
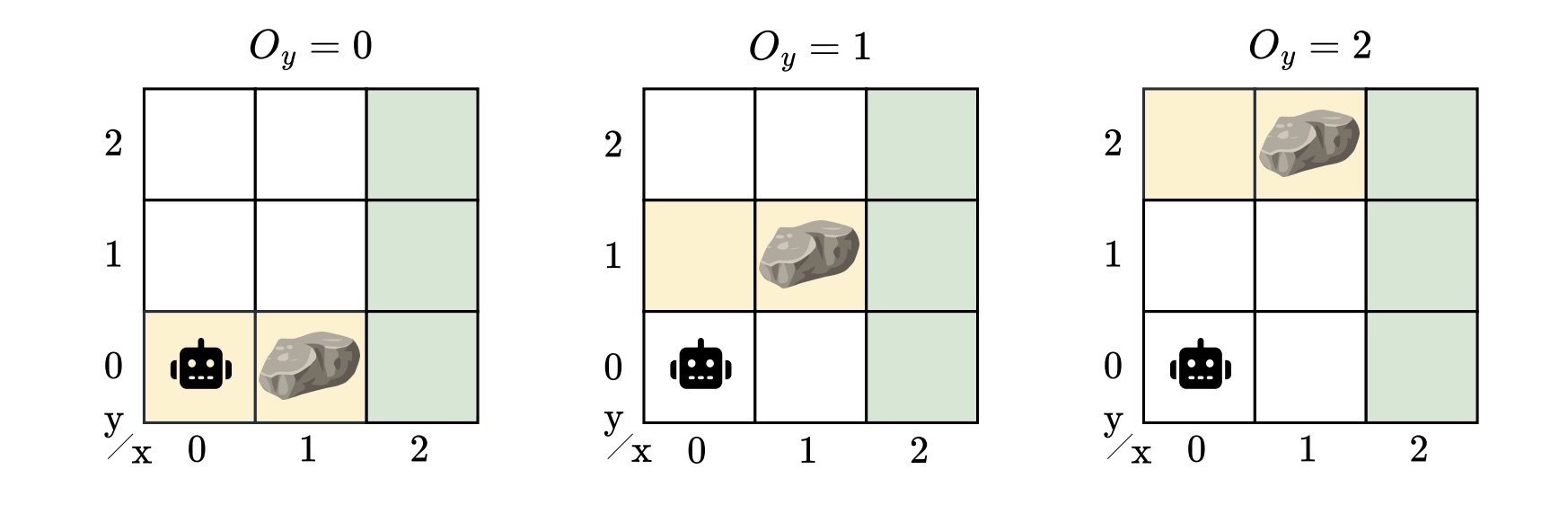
We tested rfPG on HM-POMDPs that simulated environments with uncertainty. For example, navigation problems where obstacles or sensor errors varied between models. In these tests, rfPG produced policies that were not only more robust to these variations but also generalized better to completely unseen environments than several POMDP baselines. In practice, that implies we can render controllers robust to minor variations of the model. Recall our running example, with a robot that navigates a grid-world where the rock’s location is unknown. Excitingly, rfPG solves it near-optimally with only two memory nodes! You can see the controller below.

By integrating model-based reasoning with learning-based methods, we develop algorithms for systems that account for uncertainty rather than ignore it. While the results are promising, they come from simulated domains with discrete spaces; real-world deployment will require handling the continuous nature of various problems. Still, it’s practically relevant for high-level decision-making and trustworthy by design. In the future, we will scale up — for example, by using neural networks — and aim to handle broader classes of variations in the model, such as distributions over the unknowns.
Want to know more?
Thank you for reading! I hope you found it interesting and got a sense of our work. You can find out more about my work on marisgg.github.io and about our research group at ai-fm.org.
This blog post is based on the following IJCAI 2025 paper:
- Maris F. L. Galesloot, Roman Andriushchenko, Milan Češka, Sebastian Junges, and Nils Jansen: “Robust Finite-Memory Policy Gradients for Hidden-Model POMDPs”. In IJCAI 2025, pages 8518–8526.
For more on the techniques we used from the tool PAYNT and, more generally, about using these techniques to compute FSCs, see the paper below:
- Roman Andriushchenko, Milan Češka, Filip Macák, Sebastian Junges, Joost-Pieter Katoen: “An Oracle-Guided Approach to Constrained Policy Synthesis Under Uncertainty”. In JAIR, 2025.
If you’d like to learn more about another way of handling model uncertainty, have a look at our other papers as well. For instance, in our ECAI 2025 paper, we design robust controllers using recurrent neural networks (RNNs):
- Maris F. L. Galesloot, Marnix Suilen, Thiago D. Simão, Steven Carr, Matthijs T. J. Spaan, Ufuk Topcu, and Nils Jansen: “Pessimistic Iterative Planning with RNNs for Robust POMDPs”. In ECAI, 2025.
And in our NeurIPS 2025 paper, we study the evaluation of policies:
- Merlijn Krale, Eline M. Bovy, Maris F. L. Galesloot, Thiago D. Simão, and Nils Jansen: “On Evaluating Policies for Robust POMDPs”. In NeurIPS, 2025.









