Galaxies on graph neural networks

By Yesukhei Jagvaral

The current accelerated expansion of the universe is driven by mysterious dark energy. Upcoming astronomical imaging surveys, such as LSST at Rubin Observatory, are set to provide unprecedented precise measurements of cosmological parameters, including this dark energy, using measurements such as weak gravitational lensing. Weak lensing is measured by looking for coherent patterns in galaxy shapes, which can be caused by the fact that the cosmic matter distribution coherently distorts spacetime, affecting the appearances of nearby galaxy images in similar ways. However, there are still challenges facing cosmologists on their path from data to science. One of these challenges is the effect of intrinsic alignments – where galaxies are not oriented randomly in the sky, but rather tend to point towards other galaxies. This effect contaminates our desired weak lensing signal and can bias our measurement of dark energy. Using Graph Neural Networks, we trained Generative Adversarial Networks to correctly predict the coherent orientations of galaxies in a state-of-the-art cosmological simulation. To put it simply, we put each galaxy on a node and connected the graphs using a so-called radius nearest neighbor algorithm within each gravitationally bound group. Additionally, aside from orientations which are vector quantities, we also tested our model for scalar features, such as galaxy shapes. The model also made predictions that are in good quantitative agreement with the truth. 

What is cosmology and  weak gravitational lensing?

Cosmology is a branch of physics that studies the universe as a whole and tries to answer fundamental questions of nature, such as: what is the matter/energy content of the universe, how did the universe evolve and how did the universe begin? 

Similar to how physicists of the 19th century understood the inner workings of the internal combustion engines in terms of the statistical ensembles of molecules, modern-day cosmologists try to understand the universe in terms of the statistical ensembles of galaxies and their related observables. 

Normal and dark matter in the universe has formed structures due to gravitational collapse (i.e., small clumps of matter attract other matter until there is enough to form a gravitationally bound structure); we refer to this as the large-scale structure, and it is sensitive to how the universe has expanded over time.

From the Earth we can observe the images of distant galaxies, however, these images come to us in a distorted way, aside from camera and atmospheric effects. These distortions are caused by an effect called weak gravitational lensing. When light is traveling from the source to the observer, the nearby presence of a massive object (like a galaxy cluster) in the light’s pathway can deflect the light ray, causing distortions in the perceived image on Earth. When these distortions are small, it is called weak gravitational lensing; the images of most objects in the universe experience these minute distortions en route to us. The statistical correlations of these lensed images produced by coherent large-scale structure (i.e., the cosmic web) along the line of sight, known as cosmic shear, are used as a direct probe of large-scale structure and provide cosmological information on dark energy (Killbinger, 2015).

 What is intrinsic alignment (IA) of galaxies? 

These cosmological measurements of weak lensing suffer from a number of biases and one important bias is the intrinsic alignment of galaxies. Galaxies are not oriented randomly in the sky, but rather they tend to point toward other galaxies. In other words, galaxies have their own alignments that are intrinsic, caused by local forces acting on the galaxy; as opposed to extrinsic alignments that are caused only by how light rays are deflected as they pass through space, modifying how their images are perceived by observers. Consequently, this effect can masquerade as a weak lensing signal and contaminates our desired weak lensing signal, in the process biasing our measurement of dark energy.

Intrinsic alignments (IAs) are usually modeled analytically by parametric models, which can describe the IA effect on large scales to a good degree. However, for the upcoming era of precision cosmology, they may be too simplistic, and the underlying assumptions may not be robust. Therefore, an alternative approach, preferably non-parametric, will aid in our analysis of cosmological data by permitting us to test our sensitivity to the assumptions in parametric models. IA can be directly modeled by hydrodynamical cosmological simulations, but these simulations are too costly and cannot reach the desired volume and resolution for future cosmological surveys (Troxel and Ishak, 2015).

So what’s up with cosmological simulations?

For many years, astrophysicists and cosmologists have relied on simulations to test hypotheses and derive theoretical predictions, but recently the ever-increasing computational cost of cosmological simulations has become a limiting factor in their use. Future cosmological surveys are set to cover large areas of the sky and produce high-quality data. Unfortunately, cosmological simulations with galaxy formation/evolution processes cannot match the desired large volume and the high resolution demanded by these future surveys. Thus, it would be highly valuable to identify other ways to simulate the universe, namely running less expensive gravity-only simulations (without galaxies) and then adding galaxies in the post-processing with analytical models (Vogelsberger, 2020).

Deep learning has entered the room.

Currently, the natural sciences are rapidly adopting the advances in artificial intelligence (AI)  and many AI models have been used in astrophysical and cosmological frameworks successfully (see examples here). Particularly, a group of unsupervised deep learning methods, called deep generative models (DGM) are seeing rapid adoption across multiple fields. The DGMs are trained to learn the likelihood of a given dataset and later can be used to generate new sample data. For example, DGMs have been shown to outperform traditional numeric and semi-analytic models in accuracy or speed (Kodi Ramanah et al. 2020 , Li et al. 2021). Therefore, DGMs offer a new way to generate fast simulations, thus bypassing the traditional methods that suffer from high computational costs.  

In this work we trained a DGM on a state-of-the-art simulation (TNG100 hydrodynamical simulation from the IllustrisTNG simulation suite (Nelson et al. 2019))  with galaxy formation/evolution, to capture the relevant scalar and vector features for IA.

Why graph neural networks? 

Galaxies in the universe are sparsely scattered through space with no fixed pattern or regular geometry and do not fit with conventional approaches of fully connected layers, convolutional neural networks, or recurrent neural networks to represent the data as vectors, grids (tensors), or sequences (ordered sets), respectively. Additionally, we aim to capture the correlated alignments in a population of galaxies. Thus, graphs are a natural way to model galaxies in the universe. Graphs are defined as sets of nodes and each of the links connecting pairs of nodes. 

How to build a graph for galaxies:

1. Given a simulated set of galaxies, graphs are built by placing each galaxy on a graph node. 
2. Each node will have a list of features such as mass, central vs. satellite ID (binary column), and tidal fields. 
3. For a given group, the graphs are connected. 
4. To build the graph connection, the nearest neighbors within a specified radius for a given node are connected with signals on the graphs representing the alignments, an example is shown in Figure 1.

Figure 1. The Cosmic Web as a set of graphs. Each point here is a galaxy and the connections are made based on the radius nearest neighbor algorithm.

Model architecture

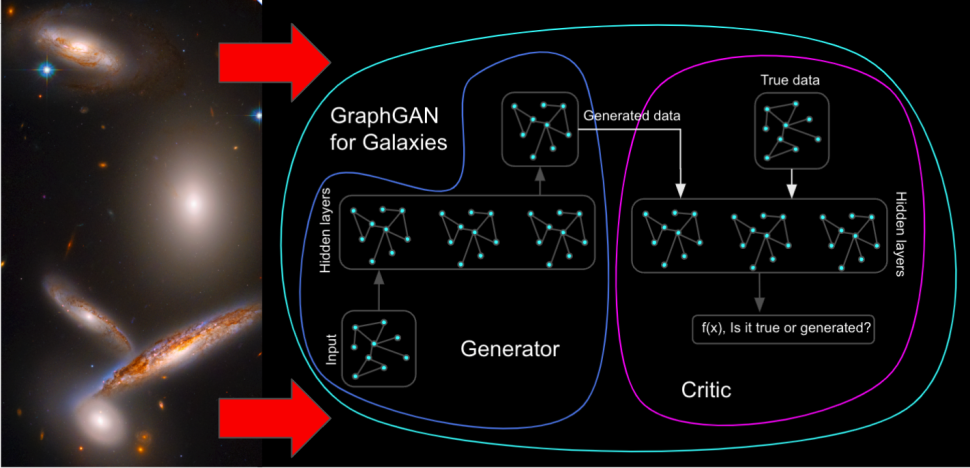
The general idea is that we have a list of features that are relevant for capturing the dependence of intrinsic alignments within a halo, and the tidal fields that are relevant for capturing the dependence of IA for galaxies on the matter beyond their halo. Then, these inputs are fed into the GAN-Generator (crimson box), which tries to learn the desired output labels (yellow box). In the end, the input and the output from the GAN-Generator are fed into the GAN-Critic (blue box) to determine the performance of the GAN-Generator.

Figure 2. The architecture of the 2D model with the inputs from the simulation.

Figure 3. A more simplified, non-technical illustration of the model architecture. credit NASA Hubble Space Telescope (The Hickson Compact Group 40).

Results: 

The figure below shows our key result: the projected two-point correlation functions ?_?+, quantifying the correlations between galaxy orientations and the positions of other galaxies as a function of their separation, for the sample we modeled. We split our sample roughly 50/50 for training and testing samples while preserving group membership of galaxies. The top rows show ?_?+ measured using data from the TNG simulation in solid lines and the data generated by the GAN in dotted lines, while the bottom panel shows the ratios as indicated by the legends.  The projected 2D correlation function, ?_?+, from the GAN agrees quantitatively with the measured one from the TNG simulation. Here, the error bars were derived from an analytic estimate of the covariance matrix. Additionally, both generated samples from the train and test sets are in good quantitative agreement with the truth values from the simulation, suggesting no overfitting.

Figure 4. Projected two-point correlation functions ??+ of galaxy positions and the projected 2D ellipticities of all galaxies split into roughly equal-sized training and testing samples while preserving group membership. The top panel shows ??+ as a function of projected galaxy separation ?? measured using data from the TNG simulation in yellow and the data generated by the GAN in dotted green, while the bottom panel shows the ratios among the curves as indicated by the label. All four curves are in good quantitative agreement, suggesting that the GAN is not significantly overfitting.

Additionally, aside from orientations which are vector quantities, we also tested our model for scalar features, such as galaxy shape parameters. The galaxy shapes are modeled as 3D ellipsoids and parameters q and s are defined as the ratio of the intermediate axis to the longest and the shortest axis to the longest (for example, a sphere would have q=s=1, whereas a pancake would have q~1 and s~0.1). For these scalar quantities, the model also made predictions to a good quantitative agreement with the truth, as shown in the Figure below. 

Figure 5. The histograms of galaxy axis ratios, defined as q=b/a (intermediate-to-major axis ratio) and s=c/a (minor-to-major axis ratio). Overall, the GAN captures and reproduces the distributions of the two axis ratios to a good degree, with the means of distributions agreeing within a few percent.

Conclusion

In this project, we developed a novel deep generative model for intrinsic alignments of galaxies. Using the TNG100 hydrodynamical simulation from the IllustrisTNG simulation suite, we have trained the model to accurately predict scalar and vector quantities of galaxies. Both for scalar and vector quantities, the GAN model generated values that were in good quantitative agreement with the distributions of their actual measured counterparts from the simulation. Learning alignment of galaxies is part of a more general problem called Galaxy-Halo connection, meaning given some properties of a dark matter halo can we predict what type of galaxy it hosts, or vice versa. We believe this is a small step toward addressing this complex problem with Graph Neural Network-based Deep Generative Model. In the future, it may be possible to generate robust full galaxy catalogs starting from halo catalogs with deep generative models. Currently there is interest among astrophysicists to pursue Graph-based Machine Learning approaches to address this high dimensional multivariate problem of Galaxy-Halo connection (Villanueva-Domingo et al. 2022).

In the future we would like to implement a similar neural network with SO(3) equivariance, also we are currently exploring how the model performs when applied to low-resolution large volume gravity only simulations. 

If you found this article to be interesting and want to learn more, we welcome you to look at our full scientific paper.

References

[1] Martin Kilbinger, Cosmology with cosmic shear observations: a review. Reports on Progress in Physics, Volume 78 086901 (2015)

[2] Michael Troxel and Mustapha Ishak. The intrinsic alignment of galaxies and its impact on weak gravitational lensing in an era of precision cosmology, Physics Reports, Volume 558, p. 1-59. (2015)

[3] Mark Vogelsberger, Federico Marinacci, Paul Torrey & Ewald Puchwein. Cosmological simulations of galaxy formation, Nature Reviews Physics volume 2, pages42–66 (2020)

[4] Doogesh Kodi Ramanah, Radosław Wojtak, Zoe Ansari, Christa Gall, Jens Hjorth. Dynamical mass inference of galaxy clusters with neural flows, Monthly Notices of the Royal Astronomical Society, Volume 499, Issue 2, (2020): 1985–1997

[5] Li, Yin, Yueying Ni, Rupert AC Croft, Tiziana Di Matteo, Simeon Bird, and Yu Feng. “AI-assisted superresolution cosmological simulations.” Proceedings of the National Academy of Sciences 118, no. 19 (2021).

[6] Nelson, Dylan, Volker Springel, Annalisa Pillepich, Vicente Rodriguez-Gomez, Paul Torrey, Shy Genel, Mark Vogelsberger et al. “The IllustrisTNG simulations: public data release.” Computational Astrophysics and Cosmology 6, no. 1 (2019): 1-29.

[7] Pablo Villanueva-Domingo, Francisco Villaescusa-Navarro, Daniel Anglés-Alcázar, Shy Genel, Federico Marinacci, David N. Spergel, Lars Hernquist, Mark Vogelsberger, Romeel Dave, and Desika Narayanan. “Inferring Halo Masses with Graph Neural Networks.” The Astrophysical Journal, 935 30

This article was initially published on the ML@CMU blog and appears here with the authors’ permission.

ML@CMU

ML@CMU