Interview with Eden Hartman: Investigating social choice problems

In their paper Reducing Leximin Fairness to Utilitarian Optimization, Eden Hartman, Yonatan Aumann, Avinatan Hassidim and Erel Segal-Halevi present a scheme for addressing social choice problems. In this interview, Eden tells us more about such problems, the team’s methodology, and why this is such a fascinating and challenging area for study.

What is the topic of the research in your paper?

The paper looks at social choice problems — situations where a group of people (called agents) must make a decision that affects everyone. For example, imagine we need to decide how to divide an inheritance among several heirs. Each agent has their own preferences over the possible outcomes, and the goal is to choose the outcome that is “best” for society as a whole. But how should we define what is “best” for society? There are many possible definitions.

Two frequent, and often contrasting definitions are the utilitarian best, which focuses on maximizing the total welfare (i.e., the sum of utilities); and the egalitarian best, which focuses on maximizing the least utility. The leximin best generalizes the egalitarian one. It first aims to maximize the least utility; then, among all options that maximize the least utility, it chooses the one that maximizes the second-smallest utility, among these — the third-smallest utility, and so forth.

Although leximin is generally regarded as a fairer approach than utilitarian, it comes at a computational cost. Calculating a choice that maximizes utilitarian welfare is often easier than finding one that maximizes egalitarian welfare, while finding one that is leximin optimal is typically even more complex.

In the paper, we present a general reduction from leximin to utilitarian. Specifically, for any social choice problem with non-negative utilities, we prove that given a black-box that returns a (deterministic) outcome that maximizes the utilitarian welfare, one can obtain a polynomial-time algorithm that returns a lottery over these outcomes that is leximin-optimal with respect to the agents’ expected utilities. Our reduction extends to approximations, and to randomized solvers. In all, with our reduction at hand, optimizing leximin in expectation is no more difficult than optimizing the utilitarian welfare.

What were your main findings?

One of the main implications of this paper is that it reveals a connection between concern for the worst-off individuals and the overall social welfare. This challenges the common perception that fairness must always come at the expense of efficiency, and instead suggests that the two can, in some cases, go hand in hand.

Could you tell us about the implications of your research and why it is an interesting area for study?

I find social choice problems fascinating because they are deeply rooted in real-life situations. The need for fairness in group decision-making is something we all experience — from small-scale situations like dividing toys among children, to large-scale decisions that affect entire populations, such as electing a president or forming a government. What makes this area particularly compelling, in my view, is the combination of real-world intuition with the beauty of mathematics — both in the modeling and formal definitions, and algorithmics — in the design of procedures that help us find decisions satisfying fairness and welfare criteria.

Today, the insights from this field are already being used in real-world systems, and even by governments, to design decision-making processes and legal frameworks that promote fairness, efficiency, and truth-telling. I find that incredibly exciting!

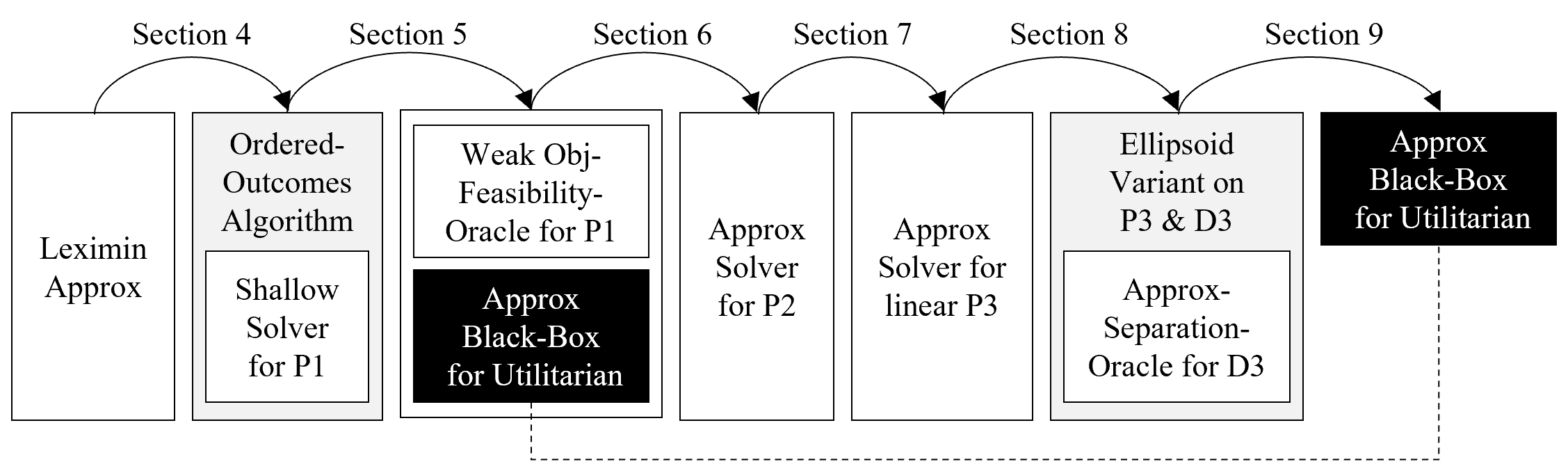A high-level description of the reduction algorithm. An arrow from element A to B denotes that the corresponding section reduces problem A to B. White components are implemented in the paper; grey components represent existing algorithms; the black component is the black-box for the utilitarian welfare.

Could you explain your methodology?

The main stages of the research began with an extensive literature review — understanding existing algorithms for finding leximin-optimal solutions, exploring different notions of approximation, and engaging in a lot of trial and error. We learned a great deal from working through concrete examples, often asking ourselves: what can we learn from this specific case?

We made progress step by step. Each time, we found a way to simplify the problem a bit more, until we eventually reached a version that can be solved using only a utilitarian welfare solver.

We brought together tools from several areas, such as – convex optimization, linear programming and duality. At one point, the approximation proof even relied on geometric series arguments. It was really satisfying to see how all the pieces came together in the end, though we didn’t know in advance what the path would look like.

I think the most important part was not giving up — even when the solution wasn’t clear at first. Every failed attempt taught us something, and those early insights were crucial to the final result.

What further work are you planning in this area?

I really enjoy working on finding good compromises. For example, in this paper, we proposed a new definition for leximin approximation and showed that it’s possible to compute such approximations, even in cases where finding an optimal solution is known to be NP-hard.

One of the research projects I’m currently working on and really excited about is in the area of truthfulness. The goal in this area is to design rule systems where all participants have an incentive to report their true preferences — or, more accurately, at least no incentive to lie. In many cases, it’s known that no rule can guarantee truthfulness from everyone. The approach we’re exploring is, again, a possible compromise: we aim to design systems where lying in a way that is both safe (never harms the agent) and profitable would require a lot of effort — specifically, the manipulator would need to gather detailed information about the preferences of others.

More broadly, I think my approach to future research is to recognize that not everything is black and white. The fact that we can’t achieve something doesn’t mean we can’t achieve anything — asking what’s within reach brings us closer, one step at a time.

About Eden

Eden Hartman is a third-year PhD student in Computer Science at Bar-Ilan University, Israel. She is advised by Professor Avinatan Hassidim (Bar-Ilan University and Google), Professor Yonatan Aumann (Bar-Ilan University), and Professor Erel Segal-Halevi (Ariel University). Her research focuses on computational social choice, specifically on fair division problems. Her work often involves defining approximation concepts, exploring meaningful compromises, and algorithmic development and analysis.

Read the work in full

Reducing Leximin Fairness to Utilitarian Optimization, Eden Hartman, Yonatan Aumann, Avinatan Hassidim, Erel Segal-Halevi, AAAI 2025.

Lucy Smith is Senior Managing Editor for AIhub.

Lucy Smith is Senior Managing Editor for AIhub.