ΑΙhub.org
Relational neurosymbolic Markov models
Image generated using Gemini 3 Nano Banana Pro.
Telling agents what to do
Our most powerful artificial agents cannot be told exactly what to do, especially in complex planning environments. They almost exclusively rely on neural networks to perform their tasks, but neural networks cannot easily be told to obey certain rules or adhere to existing background knowledge. While such uncontrolled behaviour might be nothing more than a simple annoyance next time you ask an LLM to generate a schedule for reaching a deadline in two days and it starts to hallucinate that days have 48 hours instead of 24, it can be much more impactful when that same LLM is controlling an agent responsible for navigating a warehouse filled with TNT and it decides to go just a little too close to the storage compartments.
Neurosymbolic AI to the rescue
Luckily, controlling neural networks has gained a lot of attention over the last years through the development of neurosymbolic AI. Neurosymbolic AI, or NeSy for short, aims to combine the learning abilities of neural networks with the guarantees that symbolic methods based on automated mathematical reasoning offer. Symbolic methods comprised the first wave of AI and are capable of enforcing rules and constraints, while also being great at out-of-distribution generalisation. For instance, they can learn a rule expressing that no agent can hit a box of TNT from data with only a handful of agents and boxes. However, today we have shifted more and more to neural network models, as they can be directly applied to unstructured or subsymbolic data such as images or sound waves. This shift is being challenged by NeSy, where neural and symbolic methods work together to learn and reason on any kind of data under uncertainty. In a nutshell, NeSy can be described as
NeSy = N(eural) + P(robability) + L(ogic)
Uncertainty over time
Neurosymbolic AI does however introduce some challenges, mainly because symbolic methods are notoriously computationally hard. You might be able to write down many rules of background knowledge, but checking whether the predictions of your neural network immediately satisfy these rules is often impossible with existing methods. But what if the effect of a decision only becomes apparent in the future? What if you also want to take into account uncertainty? Computing answers to this kind of probabilistic and temporally-extended questions only becomes harder. And they are important, for example if you want to measure how likely it is that your neural agent will hit those precious boxes of TNT at some point during its operation.
Relational neurosymbolic Markov models
Our paper provides a framework called relational neurosymbolic Markov models (NeSy-MMs) for dealing with complex constraints in complex environments over multiple time steps. NeSy-MMs, as the name suggest, integrate NeSy with sequential probabilistic models in the form of Markov models. This integration (1) unlocks scalable learning and reasoning for sequential applications, (2) has the advantage of supporting both discriminative and generative tasks, and (3) allows us to deal with uncertainty on discrete and continuous variables.
But how do these NeSy-MMs look like and what sets them apart from regular Markov or NeSy models? The key difference lies in the central representation of NeSy-MMs: probabilistic models over relations (Figure 1). Relations are a structured or symbolic data type that neatly captures certain data properties. For instance, the relation hit(robot, tnt) might indicate that one of our robots hit a container of TNT. If the relation hit(robot, tnt) is true, you can imagine a logical consequence could be the relation destroyed(robot) and potentially even destroyed(warehouse). Such type of relational logic is at the centre of our NeSy-MMs. While relational logic is also used by other NeSy system, we decompose relations over time similar to how planning algorithms work. Decomposing over time is also at the centre of Markov models, but they use unstructured representations rather than relational logic.
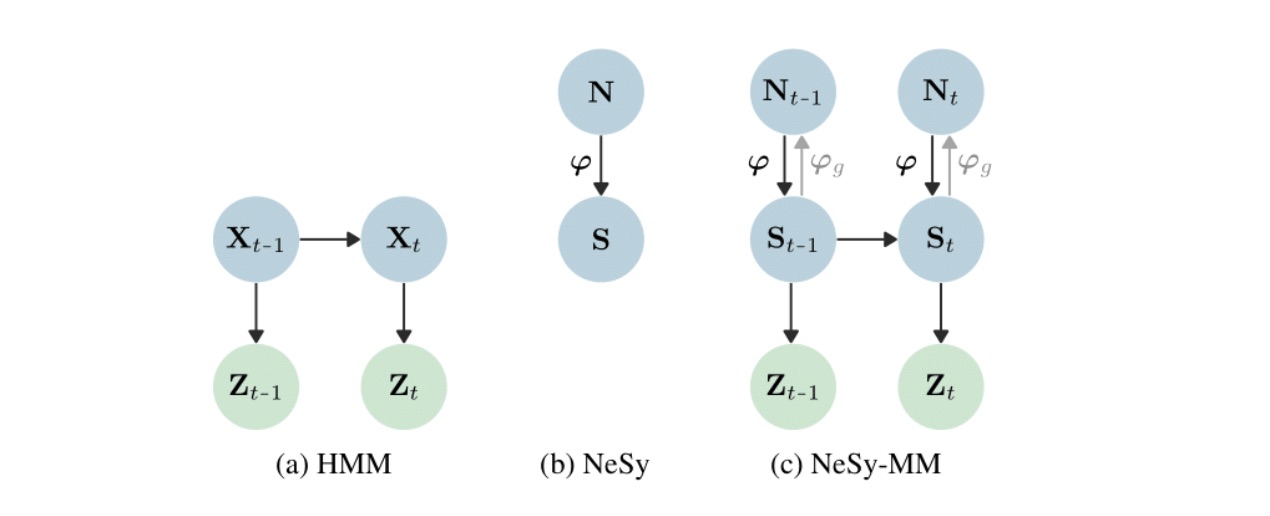
Figure 1. This figure depicts the probabilistic graphical model version of (a) an hidden Markov model, (b) a neurosymbolic model, and (c) our NeSy-MM.The key difference between an HMM (a) and a NeSy-MM (c) is that states in a NeSy-MM are symbolic relations instead of latent variables.
What do NeSy-MMs give us?
But what now? What can we do with these fancy new NeSy-MMs that we could not do before? We will give three key abilities of NeSy-MMs that other models do not have. (1) NeSy-MMs can generate content that is consistent with certain rules, (2) they scale the out-of-distribution generalisation of NeSy to non-trivial time horizons and (3) they are intervenable at test-time without requiring any retraining. These abilities will be showcased using MiniHack [1], a flexible framework around the open-ended game NetHack (Figure 2), to avoid hurting any actual robots.
Figure 2. MiniHack allows for generating complex environments with hundreds of different entities and a wide range of possible challenges and goals.
First up is consistent generation. We start from sequences of images where an agent moves around a simple, empty room for a number of steps. The knowledge we have is simple: the agent can only move one tile per time step going up, down, left or right. Given the success of generative AI (GenAI) in the last couple of years, one would expect this task to be easy for any GenAI model. Sadly, it is not; we compare NeSy-MMs to Deep Markov models, which do not use relational logic as their core representations, and a visual transformer, which uses a transformer architecture to update the game state over time. Of all models trained on the exact same data, only NeSy-MMs, where the knowledge is enforced on the model, are capable of generating new sequences that follow the navigation rules (Figure 3).
Figure 3. On the left, deep Markov models have a hard time capturing the precise location of the agent leading to generations where a superposition of possible agents is moved erratically around the room. On the right, the visual transformer generated mostly very crisp images, but it completely fails to capture the dynamics. In the middle, our NeSy-MMs generate crisp and consistent images.
Second comes out-of-distribution generalisation. Here, we make the setting more interesting by starting from sequences where the agent moves around a room containing enemy monsters (Figure 4). We keep assuming to know the navigation rules for the agent itself, but we do not know the behaviour of the monsters. Instead, this gap in our knowledge will be learned by a neural network. That is, the NeSy-MM needs to learn the transition behaviour of monsters from just sequences of interactions. These sequences are no longer images, but the symbolic game state, to give all methods access to the same precise information. We again compare NeSy-MMs to deep Markov models and a transformer model by training all models on the same 10×10 grid containing only one enemy using sequences of length 10 and testing on sequences of larger grids, more enemies and longer time horizons (Figure 5).
Figure 4. The player navigates through a room filled with enemies for a number of steps and can be killed by the enemies during their exploration.
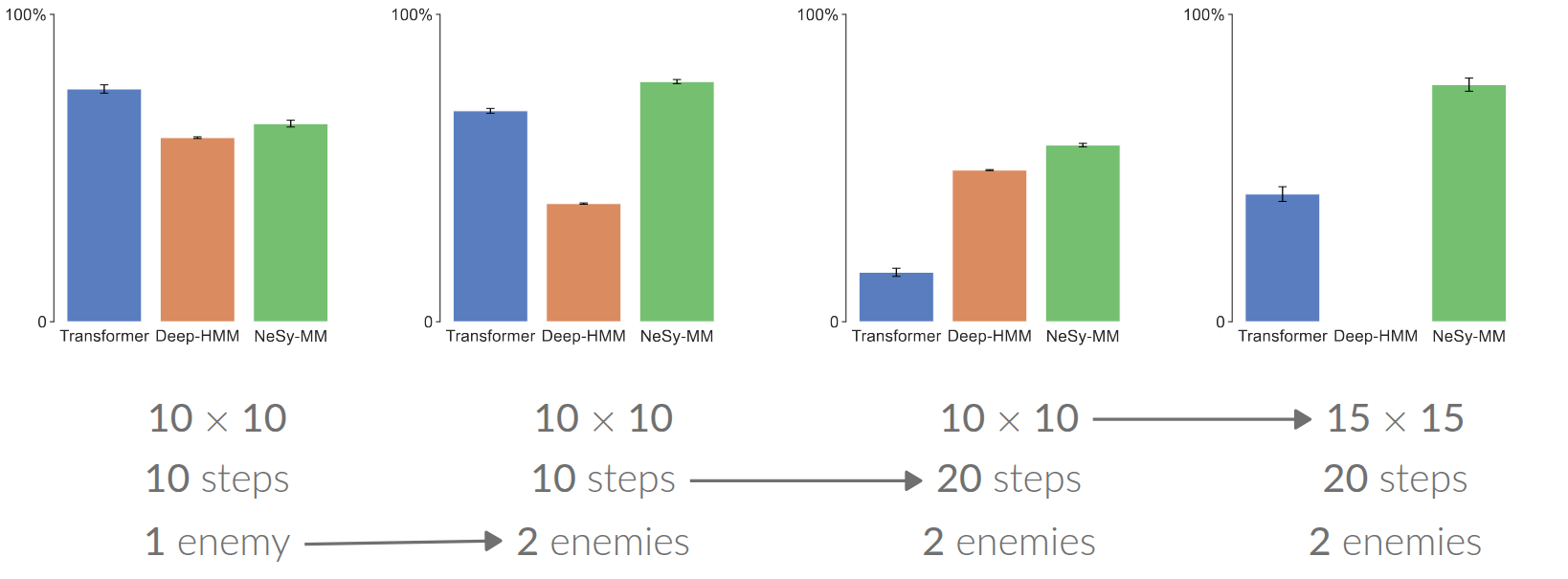Figure 5. While transformers perform best on the training data where one enemy interacts with just one enemy on a small grid, their performance does not hold up during longer interactions on larger grids with more enemies. NeSy-MMs are the only model that seem to have been able to learn representations that are robust out of distribution.
Finally, NeSy-MMs are the only model among all tested models that are intervenable, because they can change their relational logic at test time. Specifically, we take our trained generative model from earlier and add a constraint that the agent should never move to the right half of the room, even if the given actions would tell it to do so. This constraint was never seen during training, but can be added to the NeSy-MM at any time, as it is just another form of background knowledge that further constrains the relational representations of the NeSy-MM (Figure 6). No other model can be changed to a similar degree without at least being retrained on a dataset where this constraint is already present.
Figure 6. NeSy-MMs are uniquely intervenable; if the player is suddenly forbidden to enter the right two columns, then the model will adapt its generations accordingly by blocking the agent from going there.
To summarise, NeSy-MMs are a powerful class of probabilistic neurosymbolic models that can augment existing neural models with all the benefits of relational reasoning. So if you care about consistent generation or flexibly enforcing constraints on sequential data, then you should try out NeSy-MMs instead of plain neural models. Instead of trying to make the neural model behave as you want through optimisation, why not take a NeSy-MM and directly tell it what you want? Our code is openly available and you can always reach us by email (Lennert and Gabriele) for questions or feedback. You can find more neurosymbolic work on our personal websites (Lennert and Gabriele) and below.
Related work
- Exact dynamic inference and learning with many dependencies
- Approximate probabilistic learning of discrete representations
- Neurosymbolic reinforcement learning for safety in action
- Neurosymbolic system for discrete and continuous domains
tags: AAAI, AAAI2026
AIhub is supported by:
