The limitations of limited context for constituency parsing

By Yuchen Li

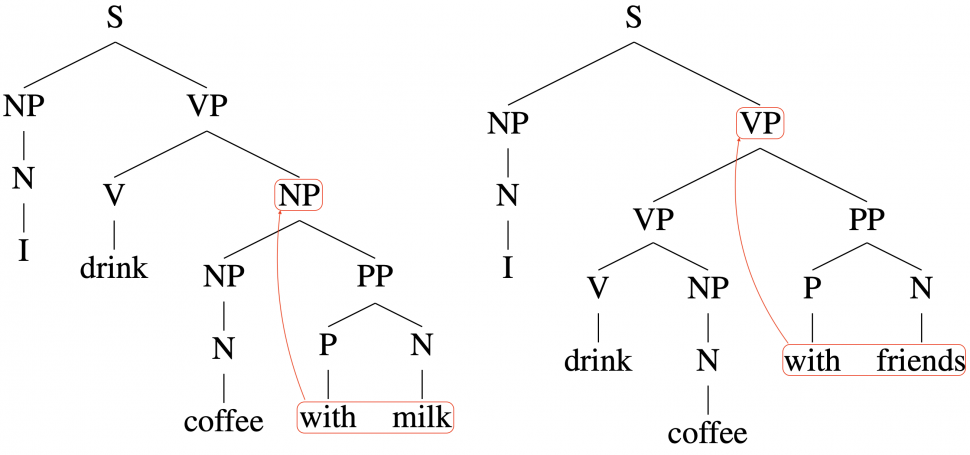
Compare the above two sentences “I drink coffee with milk” and “I drink coffee with friends”. They only differ at their very last words, but their parses differ at earlier places, too. Now imagine you read sentences like these. How well can you parse such sentences without going back and forth? This might be a daunting task when the sentences get longer and their structures more complex. In our work, we show that this task is also difficult for some leading machine learning models for parsing.

Introduction

Syntax, which roughly refers to the rules behind the composition of words into sentences, is a core characteristic of language. Hence, a central topic in natural language processing is concerned with the ability to recover the syntax of sentences. In recent years, rapid progress has been made on learning the constituency structure (one type of syntax), typically with some carefully designed syntax-aware neural network architectures. However, these architectures tend to be quite complex. It remains unclear why they work and what might be limiting their potential. In our ACL 2021 paper, we theoretically answer the question: what kind of syntactic structure can current neural approaches to syntax represent?

As an overview, our results assert that the representational power of these approaches crucially depends on the amount and directionality of context that the model has access to when forced to make each parsing decision. More specifically, we show that with full context (unbounded and bidirectional), these approaches possess full representational power; on the other hand, with limited context (either bounded or unidirectional), there are grammars for which the representational power of these approaches is quite impoverished.

How do we reason about a “ground truth” syntactic structure the model should recover?

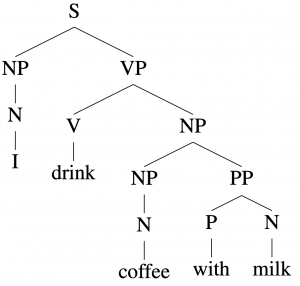
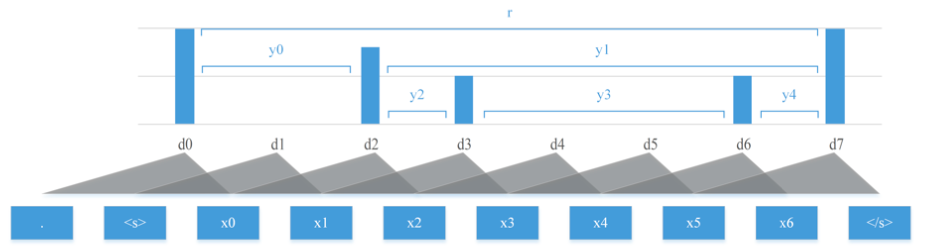
In constituency parsing, given a sentence such as “I drink coffee with milk”, we aim to obtain its parse tree as shown in Figure 1 below.

In order to have a notion of a ground truth, we assume that the data in our model is generated from a probabilistic context-free grammar (PCFG). Recall that a context-free grammar (CFG) ? is a four-tuple (Σ, ?, ?, ?), in which

• Σ is the set of terminals
• ? is the set of non-terminals
• ?∈? is the start symbol
• ? is the set of production rules of the form 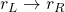, where 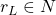, and 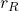is a sequence of Σ and ?

As shown in Figure 1 above, each parse tree in ? can be thought of as recursively applying a list of production rules to expand the start symbol ? to a sentence (a sequence of terminals). For each sentence, there is a set of possible parse trees leading to this sentence.

Building upon CFG, a probabilistic context-free grammar (PCFG) assigns a conditional probability to each rule . As a consequence, each parse tree is associated with a probability, which is the product of its rule probabilities. Furthermore, each sentence generated by a PCFG has a max likelihood parse (unless there is a tie).

With PCFG as the ground truth of syntax, we refine our question to ask: when is a “framework for parsing” able to represent the max likelihood parse of a sentence generated from a PCFG? In our paper, we consider frameworks based on syntactic distance and transition-based parsers. In the following sections, we introduce each framework and our corresponding analyses.

Framework 1: syntactic distance-based parsing

Background

This framework is introduced by the Parsing-Reading-Predict Network (PRPN) architecture (Shen et al., 2018).

Let be the sentence consisting of ? tokens (words). Additionally, is the sentence start symbol.

As shown in Figure 2, this framework requires learning/training a syntactic distance function between adjacent words and , for all . Here, is the context that   takes into consideration. (The vertical bar does not mean a conditional distribution; rather, the notation is just for convenience.) In PRPN, the function is parametrized by a shallow convolutional neural network and can be trained using the language modeling objective.

During inference time, given a sentence, we apply the learned network to compute the syntactic distance between each pair of adjacent words, and produce a parse tree based on greedily branching at the point of largest syntactic distance. In brief, the tree induction algorithm consists of the following steps:

1. Initialize the root to contain the whole sentence
2. Whenever there exists a single segment consisting of two or more words, split at the point with the largest syntactic distance
3. Return the binary tree whose leaves each contains one single word

For algorithmic details, please refer to Shen et al., (2018) or our paper. It suffices, for the sake of our analysis, to note that with any given sequence of syntactic distances , the tree induction algorithm is deterministic. Therefore, the representational power of this framework is determined by the ability to learn a good sequence of syntactic distances.

Our analysis

With PCFG as the “ground truth” syntactic structure, we now define what it means to represent a PCFG using the syntactic distance.

Definition: Let ? be any PCFG in Chomsky Normal Form. A syntactic distance function ? is said to be able to ?-represent G, if, for a set of sentences in ?(?) whose total probability is at least ?, the syntactic distance function ? can correctly induce the max likelihood parse of these sentences unambiguously.

Remark: Here, ambiguities could occur if e.g. , in which case we need to break ties when parsing the segment .

Positive result

With this definition, we proceed to our positive result, corresponding to parsing with full context.

Theorem 1: for sentence , let . For each PCFG in Chomsky normal form, there exists a syntactic distance measure  that can 1-represent G.

Remark: This theorem states that, when the context at each position includes the whole sentence and the current positional index, then the syntactic distance approach has full representational power.

Proof idea: Let binary tree be the max likelihood parse tree of , such as the one shown in Figure 3 above. With being the full context, is allowed to depend on the entire ground truth . Therefore, we simply need to find an assignment of such that their order matches the level at which the branches split in .

Intuitively, as shown in Figure 3, if we assign larger distance values at positions where the tree splits at higher levels, then the sequence of distances can induce the correct tree structure. To formalize this idea, set

and the deterministic tree induction algorithm would return the desired parse tree .

Negative result

In the above, we saw that parsing with full context leads to full representational power. On the other hand, as we will see next, if the context is limited, i.e., it includes everything to the left and additionally a finite look-ahead window of size to the right, then the representational power is quite impoverished.

Theorem 2: Let . ∀?>0, ∃ PCFG G in Chomsky normal form, such that any syntactic distance measure cannot ?-represent G.

Note that this theorem analyzes left-to-right parsing. A symmetric result can be proven for right-to-left parsing.

Proof idea: How would you “fool” a model which infers the syntactic distance at each position solely based on the left context?

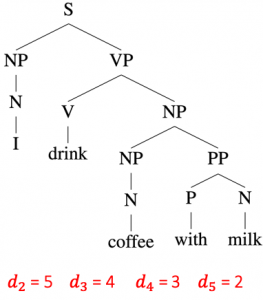
Intuitively, such models would have a hard time if the later words in a sentence can force different syntactic structures earlier in the sentence. For example, as shown in Figure 4, consider the two sentences: “I drink coffee with milk” and “I drink coffee with friends”. Their only difference occurs at their very last words, but their parses differ at some earlier words in each sentence, too.

When a “left to right” model reads the first several words of such sentences, (e.g. “I drink coffee with”), the model does not know what word (e.g. “milk” or “friend”) would come next, so our above intuition suggests that it cannot know how to parse the part of the sentence (e.g. “I drink coffee with”) that it has already read so far.

In fact, this intuition holds even if we allow the model to have a finite look-ahead to the right. Imagine the case when a sentence is long, then even if the model can peek at a handful of words ahead, it still only has access to the left portion of the sentence, while the unknown rightmost portion might actually potentially be critical for determining the structure of the sentence.

We formalize this intuition using a PCFG. This motivates our definition of the family of counterexample grammar, which is shown in Figure 5 below. Note that any two strings in the grammar are almost the same except for the last token: the prefix is shared among all strings. However, their parses differ with respect to where is split. The clue to such a difference in parse lies in the very last token , which is unique to each string.

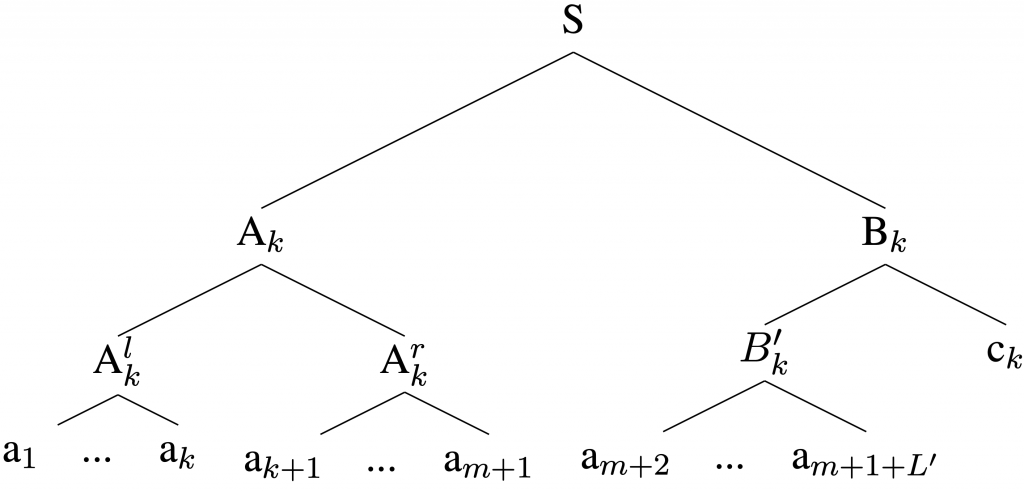
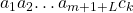For details of this counterexample grammar, please refer to our paper. It can be shown that with , for any positive integer , this grammar (parameterized by m) only allows a fraction of its language to be represented by the syntactic distance measure . It suffices to set , forcing the accuracy to be at most , which is less than .

Applying our analysis to another related architecture

Our analysis of syntactic distance-based frameworks also applies to the Ordered Neurons LSTM (ON-LSTM) architecture, proposed in Shen et al., (2019).

As shown in Figure 6 above, the ON-LSTM architecture requires training some carefully structured gate vectors at each position, using the language modeling objective. During inference time, we pass the sentence to the trained ON-LSTM, obtain the gates, and reduce the gate vectors to scalars representing the syntactic distances, and finally induce the parse tree by greedily branching as described above.

Similar results and proofs apply to ON-LSTM: with full context comes full representational power, whereas, with limited context, the representational power is also quite limited.

Framework 2: transition-based parsing

At each step, instead of a scalar (syntactic distance), we can output parsing transitions. This type of parser consists of a stack (initialized to empty) and an input buffer (initialized with the input sentence). At each position ?, based on the context at ?, the parser outputs a sequence of parsing transitions, each of which can be one of the following (based on the definition by Dyer et al., (2016) who proposed a successful neural parameterization of these transitions.)

1. NT(X): pushes a non-terminal X onto the stack.
2. SHIFT: removes the first terminal from the input buffer and pushes onto the stack.
3. REDUCE: form a new constituent based on the items on the stack

For details regarding the parsing transitions, please refer to our paper or Dyer et al., (2016).

Our analyses show that similar results, analogous to the above theorems for syntactic distance-based approaches, also hold for transition-based parsers. On the positive side, i.e., with full context, transition-based parsers have full representational power for any PCFG in Chomsky normal form. In contrast, on the negative side, i.e., if the context is bounded in one (or both) direction(s), then there exists a PCFG such that the accuracy of transition-based parsers can be made arbitrarily low. For detailed theorem statements, please refer to Section 7 of our paper.

So far we have seen our analyses on the representational power for both syntactic distance and transition-based frameworks. Why do we choose to consider these frameworks?

Remarks on frameworks considered

RNN, in its most general form, can be proved to be Turing-complete (Siegelmann and Sontag, 1992). However, the construction in Siegelmann and Sontag, (1992) may require potentially unbounded time and memory.

On the other hand, the one-pass RNN, in which the context at each position is precisely everything to the left, can be proved to have similar power to finite-state automaton (Merrill, 2019), which is insufficient for parsing PCFGs.

In our work, we consider an intermediate setting, which is more general than the simple one-pass RNN, because when the parsing decision at each word is calculated, the context can include not only everything to the left but also a finite look-ahead (to the right). Note that the look-ahead is finite, but not unbounded. Hence, the context is still limited, corresponding to our negative results. If, on the other hand, unbounded context is allowed in both directions, then the setting falls into the category of unlimited context, leading to our positive result.

While we consider the syntactic distance and transition-based frameworks because their neural parameterizations achieved strong empirical results and are representative of two general approaches to parsing, it is worthwhile to point out that our analyses are architecture-dependent. Indeed, there are some other architectures that escape the limitations we proposed, such as the Compound PCFG (Kim et al., 2019). Its parameterization is again quite complex, but one aspect to note is that, in the process of constructing a tree given a sentence, the model has information from both the left and the right and therefore its representational power is not limited by the context.

Summary

In this work, we considered the representational power of two important frameworks for constituency parsing — i.e., frameworks based on learning a syntactic distance and learning a sequence of iterative transitions to build the parse tree — in the sandbox of PCFGs. In particular, we show that if the context for calculating distance or deciding on transitions is limited on at least one side (which is often the case in practice for existing architectures), then there are PCFGs for which there is no good way to choose the distance metric or sequence of transitions to construct the max likelihood parse.

Our analyses formalized some theoretical advantages of bidirectional context over unidirectional context for parsing. We encourage practitioners who apply ML to NLP to follow this type of simple analysis, using PCFG as a sandbox to estimate the representational power when proposing a new model. We suggest re-focusing the future efforts of the community on methods that do not fall in the category of limited representational power.

Interesting related directions of research:

1. How to augment models that have been successfully scaled up (e.g. BERT) in a principled manner with syntactic information, such that they can capture syntactic structure (like PCFGs)?
2. How to understand the interaction between the syntactic and semantic modules in neural architectures? Various successful architectures share information between such modules, but the relative pros and cons of doing this are not well understood.
3. In addition to representational power, what about the optimization and generalization aspects associated with each architecture?

References

1. Yuchen Li and Andrej Risteski. The limitations of limited context for constituency parsing. ACL 2021.
2. Yikang Shen, Zhouhan Lin, Chin-Wei Huang, and Aaron Courville. Neural language modeling by jointly learning syntax and lexicon. ICLR 2018.
3. Yikang Shen, Shawn Tan, Alessandro Sordoni, Aaron Courville. Ordered neurons. ICLR 2019.
4. Chris Dyer, Adhiguna Kuncoro, Miguel Ballesteros, and Noah A. Smith. Recurrent neural network grammars. NAACL 2016.
5. Hava T. Siegelmann and Eduardo D. Sontag. On the computational power of neural nets. COLT 1992.
6. William Merrill. Sequential neural networks as automata. ACL 2019 Workshop on Deep Learning and Formal Languages: Building Bridges.
7. Yoon Kim, Chris Dyer, and Alexander Rush. Compound probabilistic context-free grammars for grammar induction. ACL 2019.

This article was initially published on the ML@CMU blog and appears here with the authors’ permission.

ML@CMU

ML@CMU