ΑΙhub.org
Developing safe controllers for autonomous systems under uncertainty
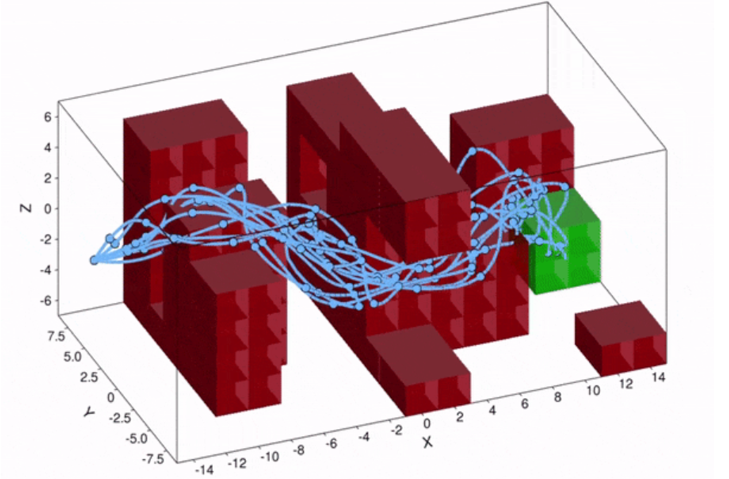
In today’s world, more and more autonomous systems operate in safety-critical settings. These systems must accomplish their task safely without the intervention of a human operator. For example, consider the unmanned aerial vehicle (UAV) in Figure 1, whose task is to deliver a package to a designated target area. The UAV should not crash into obstacles, nor should it run out of battery. In other words, the drone must behave safely.
Figure 1: The UAV’s package delivery problem.
However, turbulence or wind gusts may cause uncertainty in the position and velocity of the UAV. Such factors, also referred to as noise, render the behavior of the UAV uncertain. Consequently, the ambitious aim is to compute a controller for the UAV, such that it progresses safely to its target, despite the uncertainty. The focus of our research group is such dependable and safe decision-making under uncertainty. AI systems, such as the UAV, need to account for the inherent uncertainty in the real world autonomously. We combine state-of-the-art techniques from machine learning, artificial intelligence, control theory, and rigorous formal verification to provide strong guarantees on the safe decision-making of AI systems.
A general problem that we face is how to capture uncertainty. For problems such as the UAV delivery, existing methods rely on critical assumptions on the type of noise. For instance, a common assumption is that we have access to well-behaved probability distributions that capture the noise precisely. In practice, however, these assumptions are unrealistic, and they may even lead to unsafe behavior of the autonomous system. For example, suppose the UAV enters a location with a specific velocity. In that case, we need to know precisely the probability that a wind gust will disturb the UAV’s trajectory to compute a safe controller.
Our recent paper Sampling-Based Robust Control of Autonomous Systems with Non-Gaussian Noise follows that line of research and has been selected as a distinguished paper at AAAI. We propose the first method to compute safe controllers for autonomous systems in safety-critical settings under unknown stochastic noise. In contrast to existing methods, we do not rely on any explicit representation of this noise. Instead, we predict the outcome of actions based on previous observations of the noise, that is, our approach is sampling-based. By combining ideas from the fields of control theory, artificial intelligence, and formal verification, we can compute controllers that are safer than those computed by state-of-the-art alternatives.
Abstraction-based planning
We consider autonomous systems as continuous-state linear dynamical models, with continuous control inputs that affect the state of the overall system. The general problem that we face is to compute a feedback controller that maximizes the probability to safely reach a desired goal state, while avoiding unsafe states. This problem is very hard to solve in general, because the state and control inputs are continuous, and because the outcomes of control inputs are uncertain due to disturbances in the form of noise.
The key step in our approach is to compute a discrete-state abstraction of the continuous system. Loosely speaking, we partition the infinitely many states into a set of abstract, discrete regions. We then define abstract actions that correspond to control inputs that cause transitions between these regions. Due to the noise, every action has multiple possible outcomes that all occur with a certain probability. We compute lower and upper bounds (intervals) on these probabilities based on a finite number of observations of the noise.
Our abstraction procedure ensures that we obtain a faithful, yet abstract representation of the autonomous system. In fact, this abstraction constitutes a type of Markov decision process, which is the standard type of model in sequential decision making under uncertainty. To analyze our abstract models in a rigorous manner, we use state-of-art tools from an area called formal verification.
Solving the UAV delivery problem
Solving the UAV delivery problem
Now consider the specific UAV delivery problem in Figure 2, with the target area in green, and the obstacles that we must avoid in red. With our method, we can compute a controller, for which the probability to safely reach the target area is above a predefined safety threshold. The effect of turbulence causes a non-Gaussian stochastic disturbance that affects the 6-dimensional state of the UAV. The wind strength may vary from day to day, so the optimal path to take may differ as well. With our method, we can take this effect into account, because we reason over the effect of the turbulence explicitly. As shown in the figure, under weak turbulence, the UAV takes the short but narrow path, while under high noise, it is safer to take the longer path around the obstacles. Thus, accounting for noise is important to obtain controllers that are safe.
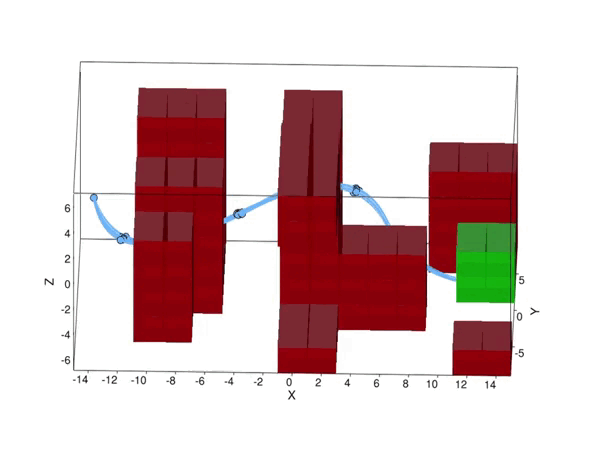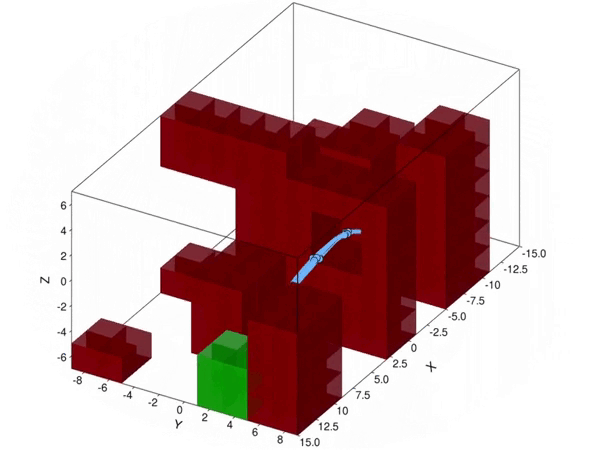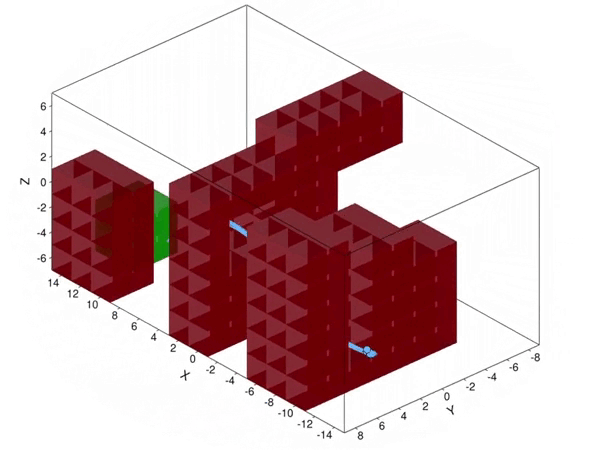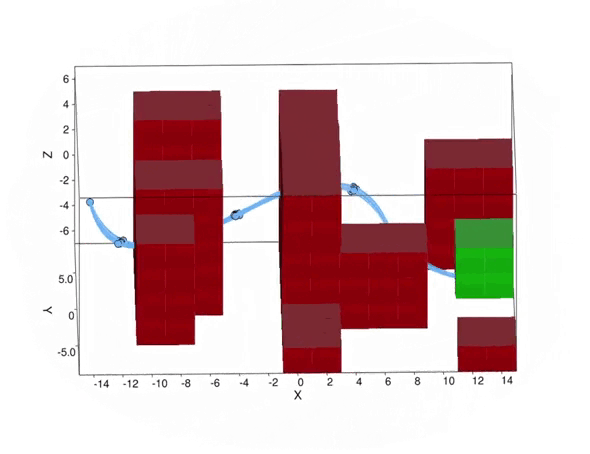
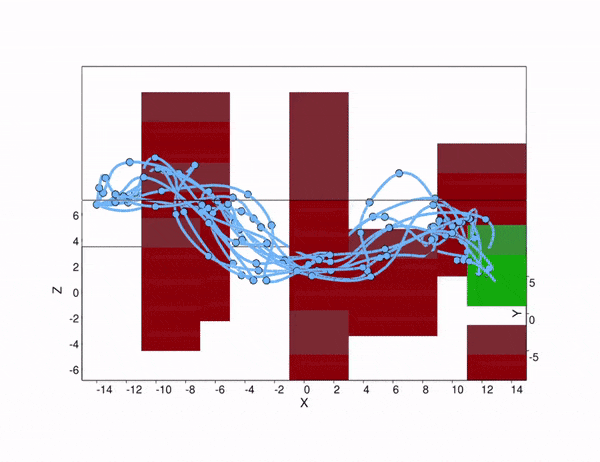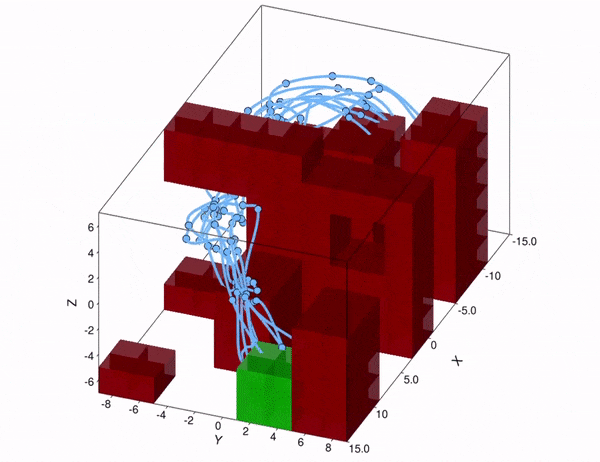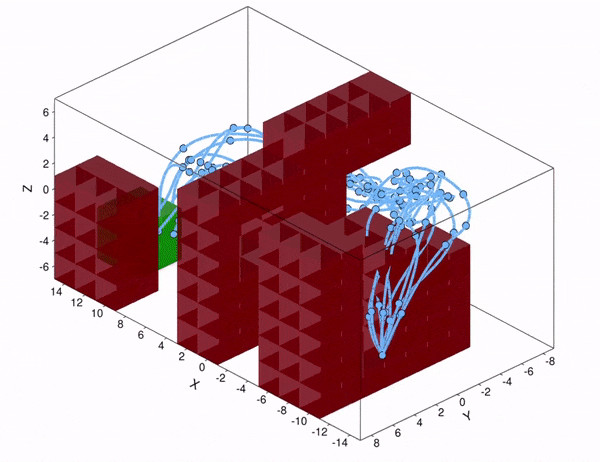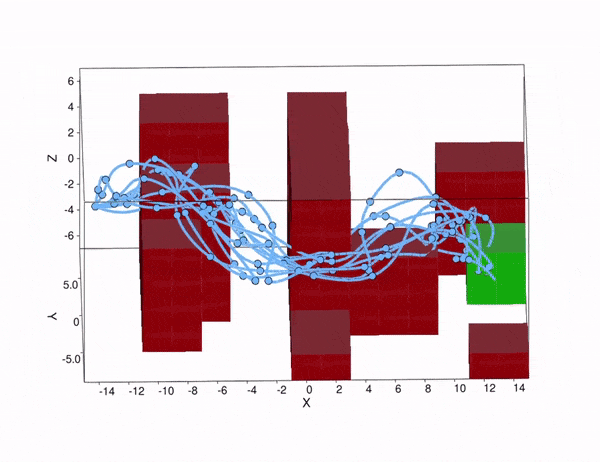Figure 2. Simulated trajectories for the UAV under different turbulence conditions. Above: low noise. Below: high noise.
Future work
Developing methods to design safe controllers is a critical necessity in a world with an increasing number of autonomous systems. When these systems operate close to human beings, guaranteeing safe behavior is of utmost importance. Designing safe controllers is particularly difficult because these autonomous systems operate in continuous and uncertain environments.
We have made a first step in designing safe controllers, even if the system is perturbed by noise of an unknown probability distribution. With our approach, we bridge the gap between continuous systems in the physical world and discrete models in computer science. As part of our ongoing research, we aim to make our algorithms even faster and apply our method to systems with different types of uncertainty. Moreover, we will continuously apply our work to new applications from areas such as robotics, fintech, or predictive maintenance.
tags: AAAI2022
AUAI is supported by:
