ΑΙhub.org
Why do policy gradient methods work so well in cooperative MARL? Evidence from policy representation
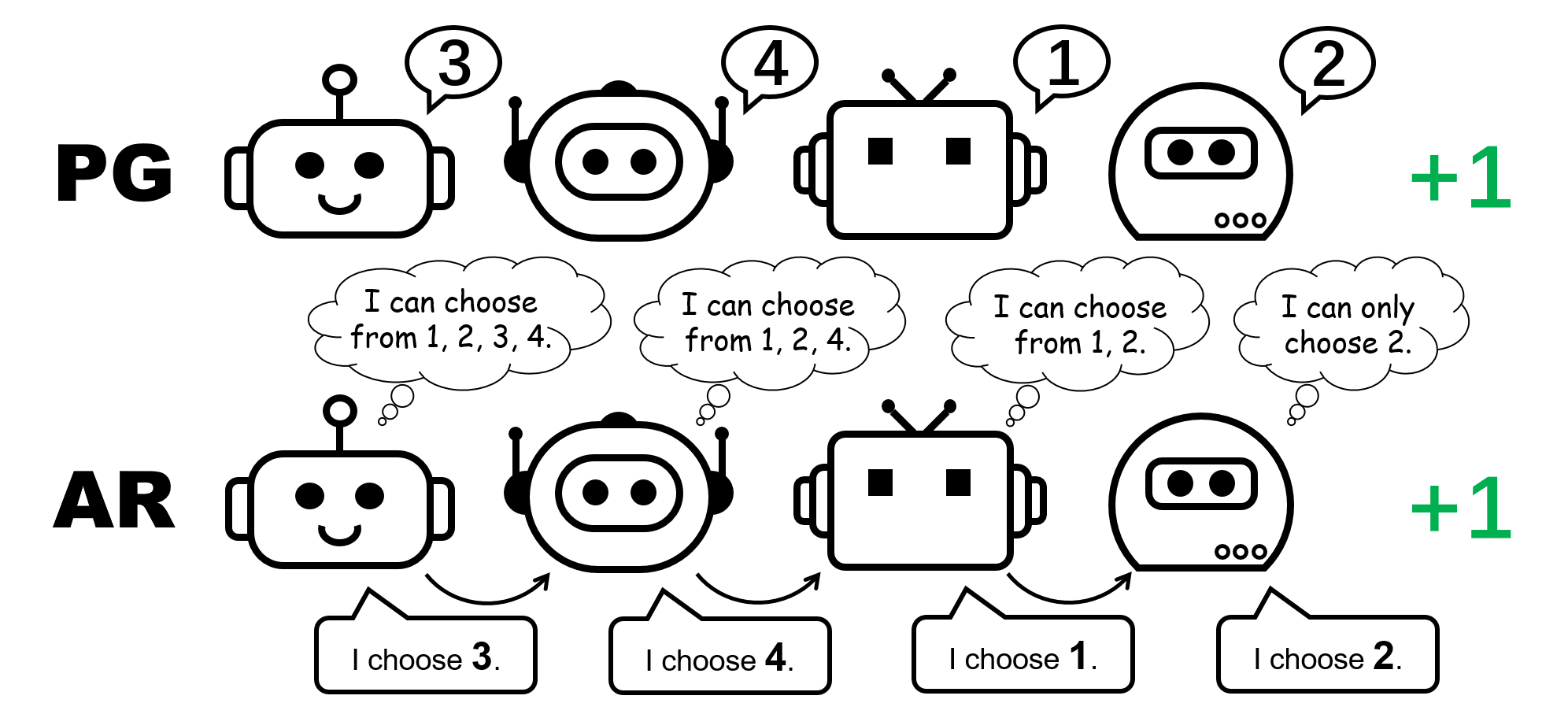Figure 1: different policy representation for the 4-player permutation game.
By Wei Fu, Chao Yu, Jiaqi Yang, Yi Wu
In cooperative multi-agent reinforcement learning (MARL), due to its on-policy nature, policy gradient (PG) methods are typically believed to be less sample efficient than value decomposition (VD) methods, which are off-policy. However, some recent empirical studies demonstrate that with proper input representation and hyper-parameter tuning, multi-agent PG can achieve surprisingly strong performance compared to off-policy VD methods.
Why could PG methods work so well? In this post, we will present concrete analysis to show that in certain scenarios, e.g., environments with a highly multi-modal reward landscape, VD can be problematic and lead to undesired outcomes. By contrast, PG methods with individual policies can converge to an optimal policy in these cases. In addition, PG methods with auto-regressive (AR) policies can learn multi-modal policies.
CTDE in Cooperative MARL: VD and PG methods
Centralized training and decentralized execution (CTDE) is a popular framework in cooperative MARL. It leverages global information for more effective training while keeping the representation of individual policies for testing. CTDE can be implemented via value decomposition (VD) or policy gradient (PG), leading to two different types of algorithms.
VD methods learn local Q networks and a mixing function that mixes the local Q networks to a global Q function. The mixing function is usually enforced to satisfy the Individual-Global-Max (IGM) principle, which guarantees the optimal joint action can be computed by greedily choosing the optimal action locally for each agent.
By contrast, PG methods directly apply policy gradient to learn an individual policy and a centralized value function for each agent. The value function takes as its input the global state (e.g., MAPPO) or the concatenation of all the local observations (e.g., MADDPG), for an accurate global value estimate.
The permutation game: a simple counterexample where VD fails
We start our analysis by considering a stateless cooperative game, namely the permutation game. In an 
-player permutation game, each agent can output actions 
. Agents receive 
reward if their actions are mutually different, i.e., the joint action is a permutation over 
; otherwise, they receive 
reward. Note that there are 
symmetric optimal strategies in this game.
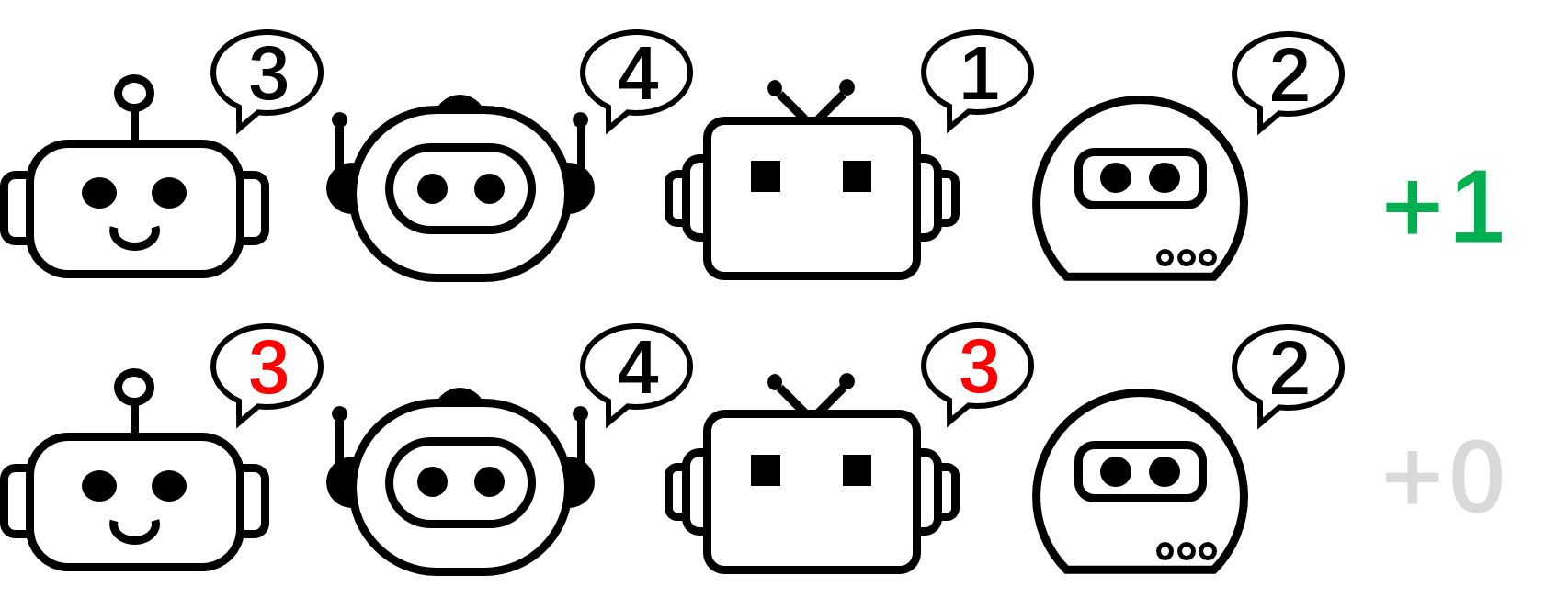
Figure 2: the 4-player permutation game.
Let us focus on the 2-player permutation game for our discussion. In this setting, if we apply VD to the game, the global Q-value will factorize to
![\[Q_\textrm{tot}(a^1,a^2)=f_\textrm{mix}(Q_1(a^1),Q_2(a^2)),\]](https://aihub.org/wp-content/ql-cache/quicklatex.com-7cbe906c4064e7c74f4789099232a35f_l3.png "Rendered by QuickLaTeX.com")
where 
and 
are local Q-functions, 
is the global Q-function, and 
is the mixing function that, as required by VD methods, satisfies the IGM principle.
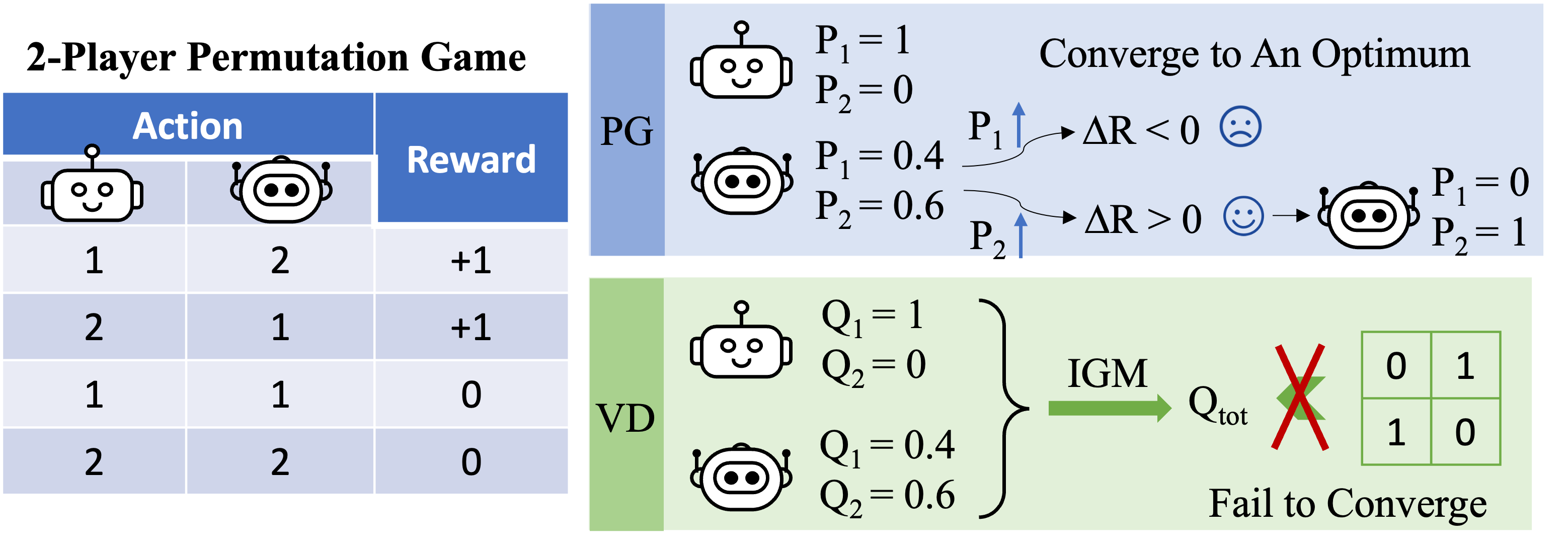
Figure 3: high-level intuition on why VD fails in the 2-player permutation game.
We formally prove that VD cannot represent the payoff of the 2-player permutation game by contradiction. If VD methods were able to represent the payoff, we would have
![\[Q_\textrm{tot}(1, 2)=Q_\textrm{tot}(2,1)=1 \qquad \textrm{and} \qquad Q_\textrm{tot}(1, 1)=Q_\textrm{tot}(2,2)=0.\]](https://aihub.org/wp-content/ql-cache/quicklatex.com-fbacf98e0b8a45e370a60629a93885d4_l3.png "Rendered by QuickLaTeX.com")
However, if either of these two agents have different local Q values, e.g. 
, then according to the IGM principle, we must have
![\[1=Q_\textrm{tot}(1,2)=\arg\max_{a^2}Q_\textrm{tot}(1,a^2)>\arg\max_{a^2}Q_\textrm{tot}(2,a^2)=Q_\textrm{tot}(2,1)=1.\]](https://aihub.org/wp-content/ql-cache/quicklatex.com-3720cf145461d912bdf0414d5f358785_l3.png "Rendered by QuickLaTeX.com")
Otherwise, if 
and 
, then
![\[Q_\textrm{tot}(1, 1)=Q_\textrm{tot}(2,2)=Q_\textrm{tot}(1, 2)=Q_\textrm{tot}(2,1).\]](https://aihub.org/wp-content/ql-cache/quicklatex.com-dcb344ca51d74548f2f54102716919a9_l3.png "Rendered by QuickLaTeX.com")
As a result, value decomposition cannot represent the payoff matrix of the 2-player permutation game.
What about PG methods? Individual policies can indeed represent an optimal policy for the permutation game. Moreover, stochastic gradient descent can guarantee PG to converge to one of these optima under mild assumptions. This suggests that, even though PG methods are less popular in MARL compared with VD methods, they can be preferable in certain cases that are common in real-world applications, e.g., games with multiple strategy modalities.
We also remark that in the permutation game, in order to represent an optimal joint policy, each agent must choose distinct actions. Consequently, a successful implementation of PG must ensure that the policies are agent-specific. This can be done by using either individual policies with unshared parameters (referred to as PG-Ind in our paper), or an agent-ID conditioned policy (PG-ID).
PG outperform best VD methods on popular MARL testbeds
Going beyond the simple illustrative example of the permutation game, we extend our study to popular and more realistic MARL benchmarks. In addition to StarCraft Multi-Agent Challenge (SMAC), where the effectiveness of PG and agent-conditioned policy input has been verified, we show new results in Google Research Football (GRF) and multi-player Hanabi Challenge.
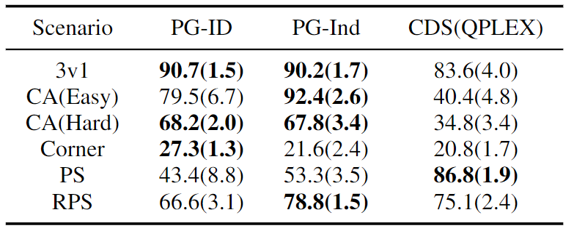
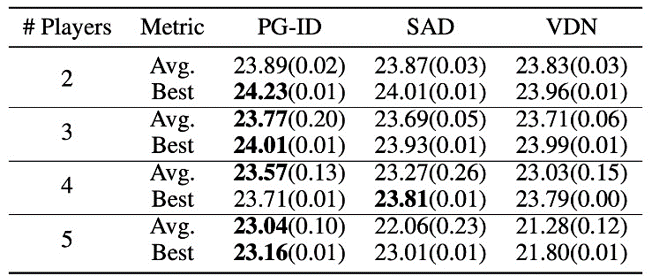
Figure 4: (top) winning rates of PG methods on GRF; (bottom) best and average evaluation scores on Hanabi-Full.
In GRF, PG methods outperform the state-of-the-art VD baseline (CDS) in 5 scenarios. Interestingly, we also notice that individual policies (PG-Ind) without parameter sharing achieve comparable, sometimes even higher winning rates, compared to agent-specific policies (PG-ID) in all 5 scenarios. We evaluate PG-ID in the full-scale Hanabi game with varying numbers of players (2-5 players) and compare them to SAD, a strong off-policy Q-learning variant in Hanabi, and Value Decomposition Networks (VDN). As demonstrated in the above table, PG-ID is able to produce results comparable to or better than the best and average rewards achieved by SAD and VDN with varying numbers of players using the same number of environment steps.
Beyond higher rewards: learning multi-modal behavior via auto-regressive policy modeling
Besides learning higher rewards, we also study how to learn multi-modal policies in cooperative MARL. Let’s go back to the permutation game. Although we have proved that PG can effectively learn an optimal policy, the strategy mode that it finally reaches can highly depend on the policy initialization. Thus, a natural question will be:
Can we learn a single policy that can cover all the optimal modes?
In the decentralized PG formulation, the factorized representation of a joint policy can only represent one particular mode. Therefore, we propose an enhanced way to parameterize the policies for stronger expressiveness — the auto-regressive (AR) policies.
Figure 5: comparison between individual policies (PG) and auto-regressive policies (AR) in the 4-player permutation game.
Formally, we factorize the joint policy of 
agents into the form of
![\[\pi(\mathbf{a} \mid \mathbf{o}) \approx \prod_{i=1}^n \pi_{\theta^{i}} \left( a^{i}\mid o^{i},a^{1},\ldots,a^{i-1} \right),\]](https://aihub.org/wp-content/ql-cache/quicklatex.com-4996f8d6a765353aca34c32c83c9dfe1_l3.png "Rendered by QuickLaTeX.com")
where the action produced by agent 
depends on its own observation 
and all the actions from previous agents 
. The auto-regressive factorization can represent any joint policy in a centralized MDP. The only modification to each agent’s policy is the input dimension, which is slightly enlarged by including previous actions; and the output dimension of each agent’s policy remains unchanged.
With such a minimal parameterization overhead, AR policy substantially improves the representation power of PG methods. We remark that PG with AR policy (PG-AR) can simultaneously represent all optimal policy modes in the permutation game.
Figure: the heatmaps of actions for policies learned by PG-Ind (left) and PG-AR (middle), and the heatmap for rewards (right); while PG-Ind only converge to a specific mode in the 4-player permutation game, PG-AR successfully discovers all the optimal modes.
In more complex environments, including SMAC and GRF, PG-AR can learn interesting emergent behaviors that require strong intra-agent coordination that may never be learned by PG-Ind.
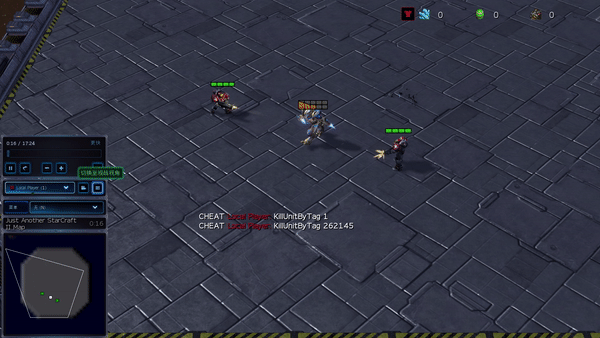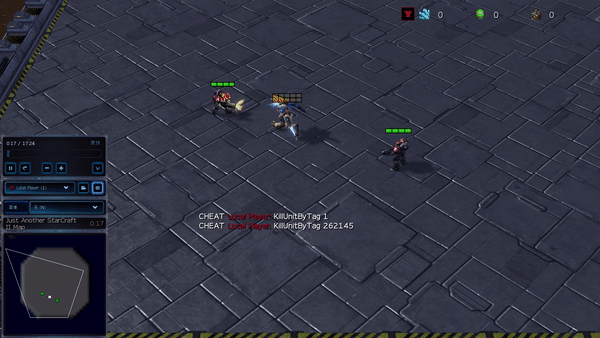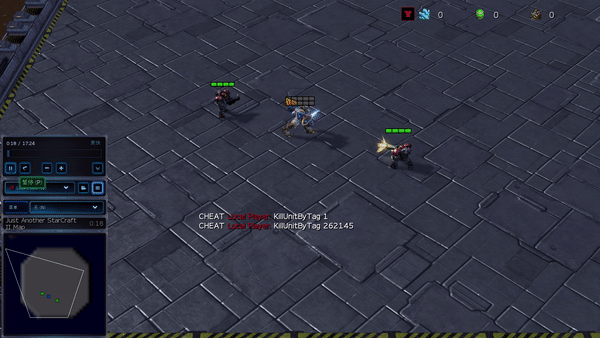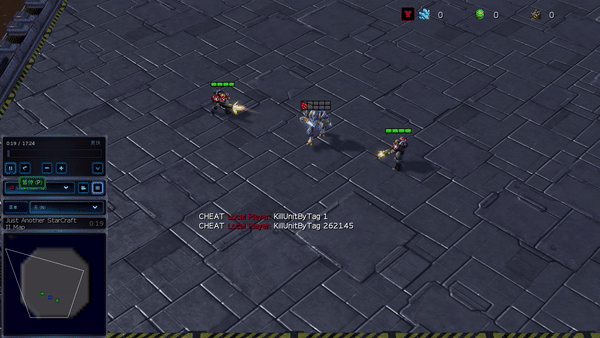
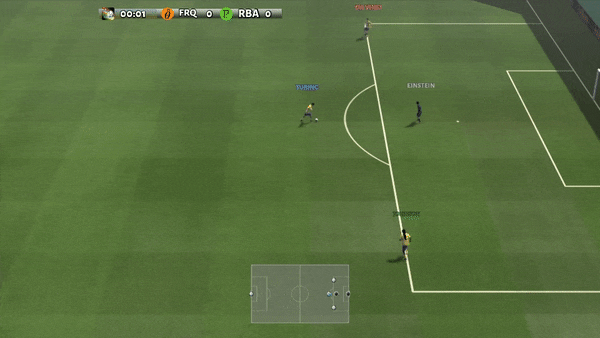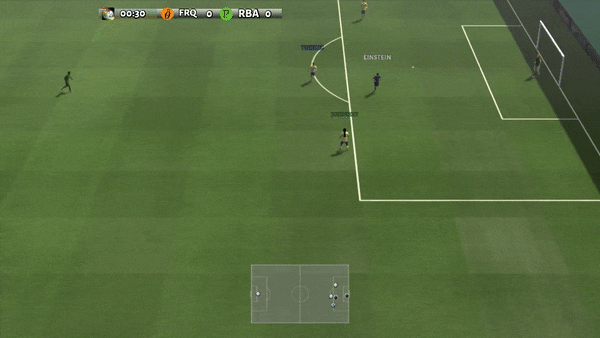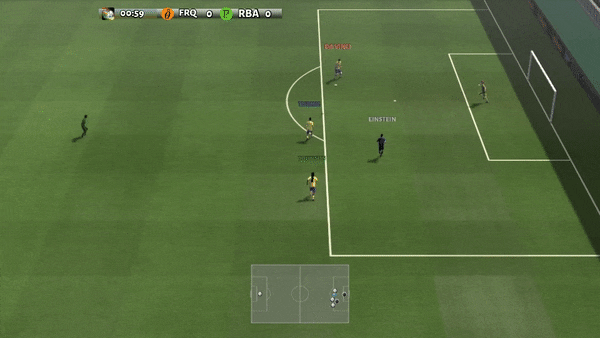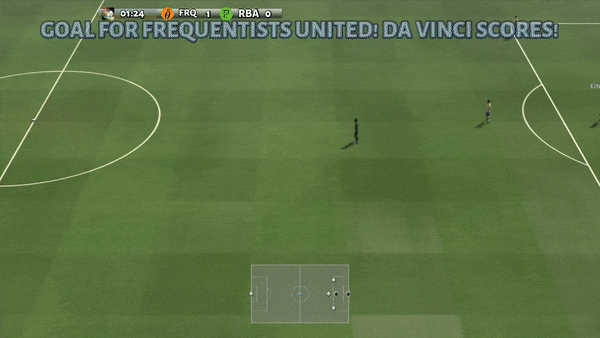
Figure 6: (top) emergent behavior induced by PG-AR in SMAC and GRF. On the 2m_vs_1z map of SMAC, the marines keep standing and attack alternately while ensuring there is only one attacking marine at each timestep; (bottom) in the academy_3_vs_1_with_keeper scenario of GRF, agents learn a “Tiki-Taka” style behavior: each player keeps passing the ball to their teammates.
Discussions and Takeaways
In this post, we provide a concrete analysis of VD and PG methods in cooperative MARL. First, we reveal the limitation on the expressiveness of popular VD methods, showing that they could not represent optimal policies even in a simple permutation game. By contrast, we show that PG methods are provably more expressive. We empirically verify the expressiveness advantage of PG on popular MARL testbeds, including SMAC, GRF, and Hanabi Challenge. We hope the insights from this work could benefit the community towards more general and more powerful cooperative MARL algorithms in the future.
This post is based on our paper in joint with Zelai Xu: Revisiting Some Common Practices in Cooperative Multi-Agent Reinforcement Learning (paper, website).
This article was initially published on the BAIR blog, and appears here with the authors’ permission.
tags: deep dive
AIhub is supported by:
