#IJCAI2022 distinguished paper – Plurality veto: A simple voting rule achieving optimal metric distortion

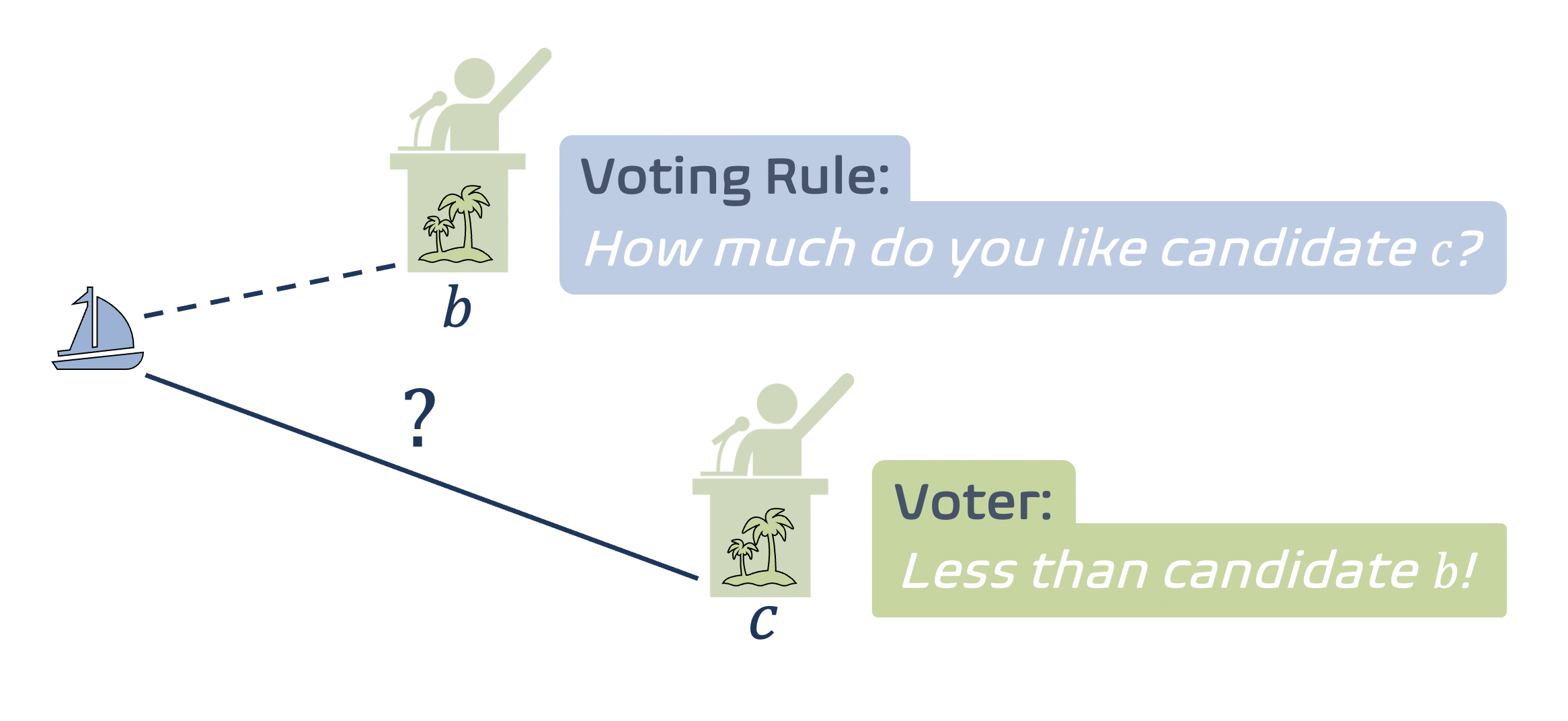
What was your answer the last time your spouse or partner asked how much you like them? Whatever your answer was, it probably did not include a unit of measurement. For most people, it is cognitively hard to tell how much they like somebody or something with objectivity. This has an invisible but crucial effect on how we humans make group decisions. Namely, due to the difficulty of quantifying strengths of preferences, as well as the potential that individuals might deliberately misrepresent strengths to manipulate outcomes, most voting systems (or group decision protocols) only elicit a ranking of alternatives from voters.

This is in sharp contrast with how group decisions are made in the animal kingdom. Just as humans, lots of other species who live in groups have their own means of reaching a consensus—bees, ants, meerkats, wild dogs and monkeys, just to name a few [1]. Unlike humans, some insects such as bees or ants seem to be good at signaling the intensity of their preferences very precisely; almost as if a number [2, 3]. They do so using a combination of involuntary behaviors such as releasing certain hormones, vibrating the body in certain frequencies and instinctual dance rituals. This makes it possible for them to reach collective decisions in a different way than humans; they can run a close approximation of utilitarian voting: each voter reports her* utility for each option and the one with the highest total utility wins.

Being able to express preference strengths fairly accurately allows groups of animals to make explicitly utilitarian decisions, choosing an option that approximately maximizes the social welfare—the sum of utilities of all individual animals. Indeed, honeybees mimic utilitarian voting to pick a nesting site; and according to entomologists, the optimal site for the survival of the colony is chosen about 90% of the time [3, 4]. The human inability to convey these strengths accurately stymies attempts to mimic this behavior; instead, most voting systems are based on ranked-choice input (rankings), and indeed, quite a lot of decisions are made based on plurality voting, where only top choices are elicited, and aggregated into a winner with the largest number of top votes. More generally, the aggregation is performed by a voting rule based on the rankings. Numerous rules have been proposed over the years, with no consensus on a “best” rule.

Metric distortion framework

The inspiration of animals’ ability to perform utilitarian voting has recently led to a fruitful new approach for defining which voting rules are “good”. Specifically, one can consider a ranking-based voting rule “good” if it mostly compensates for the lack of information on preference strengths. Of course, we do not expect a voting rule to be able to fully compensate for this lack of information, so a closely related question is “How much does the inability of voters to quantify utilities impact the social welfare?”. This question can be studied in a simple, elegant and natural way via the metric distortion framework [5,6], which I will explain now using a toy problem.

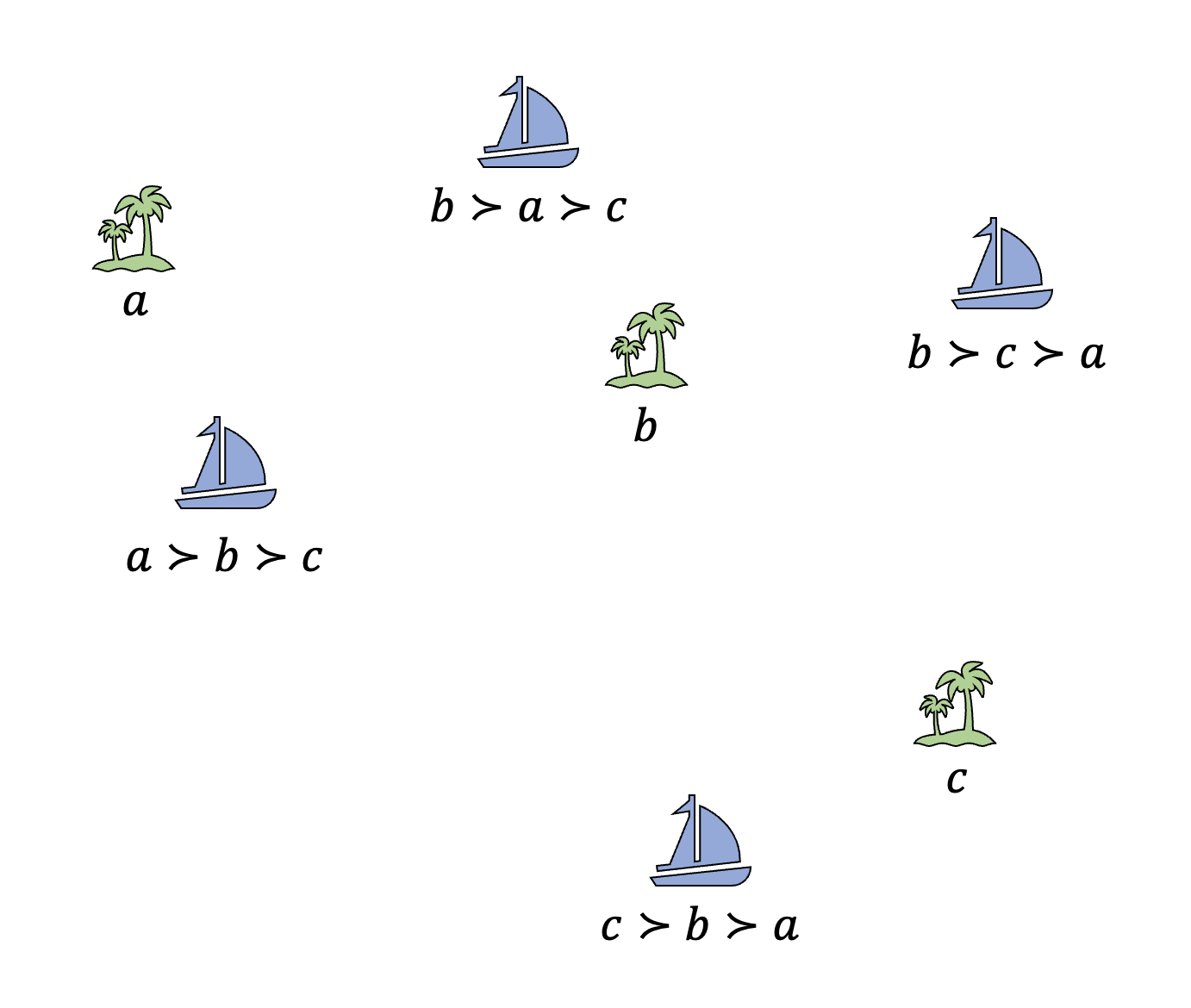
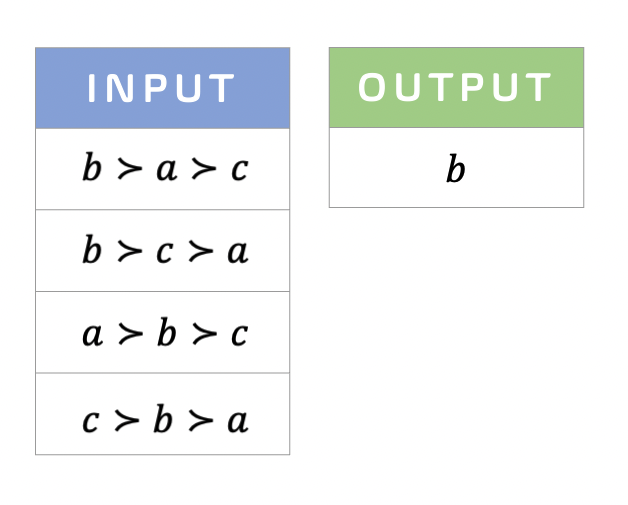
Consider the above picture with 4 ships and 3 islands. Suppose that these ships need to collectively decide on one of the islands to meet at and the goal is to minimize the total distance they travel. The crux is that ships cannot tell the exact distances between themselves and the islands. They can only rank the islands from the closest to the farthest, e.g., the ship on the left end can only tell that she is closest to a, then b, and then c. The ships jointly need to pick one of the islands given only these rankings, not the actual distances. That is, the input and the desired output of the problem is as follows.

The motivation here is that if the islands are thought of as candidates in an election, then voters run across the same problems as these ships, because voters, too, cannot express numerically how much they like a given candidate c. The best they can do is to compare candidate c with some other candidate. Moreover, the sea can be thought of as a space of opinions where voters like candidates closer to themselves more, just as in a political spectrum (or any other spatial model of voting [7]). In other words, the distance between a voter v and a candidate c represents the cost (negative utility) that voter v incurs if candidate c is picked. Hence, the goal is the same as in utilitarian voting: minimize the social cost—the total cost of voters.

To make things a bit more concrete, let us now take a sanity check: Do you think it is always possible to select the optimal island, without knowing the actual distances?

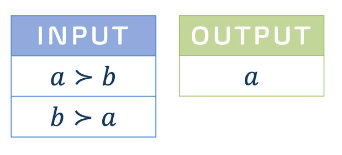
Consider the above election. There are two candidates a and b; and two voters, one of whom ranks a at the top, and the other ranks b at the top. Since a and b are symmetric, we can assume that candidate a is chosen as the winner without loss of generality.

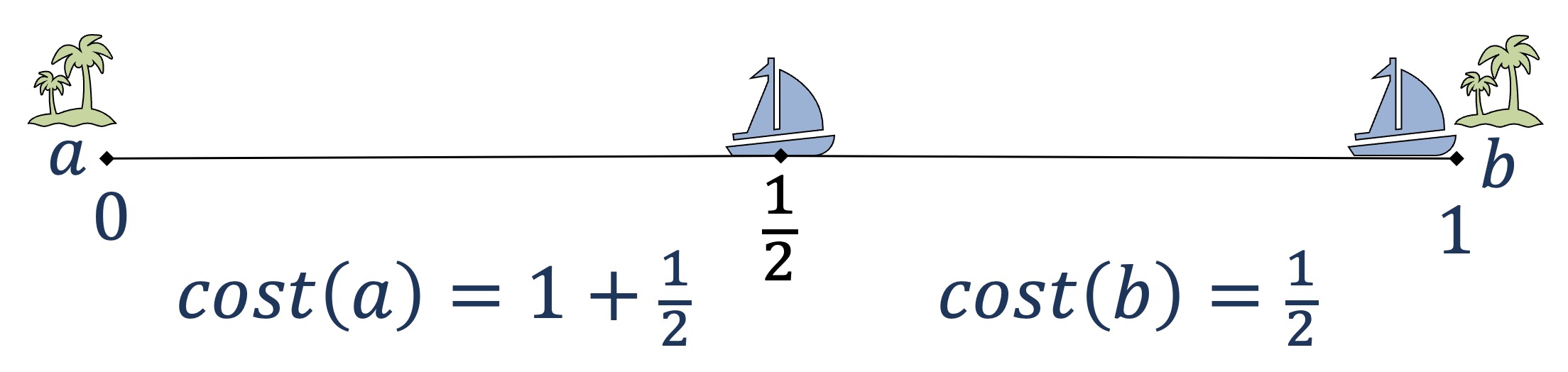
Now, imagine that voters and candidates are embedded into a 1-dimensional space as above. Notice that the distances are consistent with our input. One of the ships is much closer to b and the other is slightly closer to a. Note that these could have been the actual distances. The total distance that ships need to travel to reach island a is 1 + 1/2, which is 3/2. But we could have done 3 times better by choosing candidate b instead. This ratio, in the worst case, is called (metric) distortion. Thus, voting rules with lower distortion are better at reflecting the opinions of voters (or in other words, they are better at approximating utilitarian voting) in the worst case.

As you can see from this example it is in general not possible to beat distortion 3; because any voting rule given the above election has to make an arbitrary decision. Then, the next natural question to ask is whether there exists a voting rule that always achieves distortion no worse than 3. This question has been studied very thoroughly in the literature. Initially, the focus was on studying the distortion of well-known voting rules [5,6,8,9]. Yet all of them turned out to be suboptimal (have distortion greater than 3) and researchers started designing more sophisticated voting rules with better distortion [10]. This line of work led to a novel voting rule with distortion 3 called plurality matching due to Gkatzelis, Halpern, and Shah [11].

However, plurality matching is unusually complex for a voting rule in the conventional sense. Almost certainly, it is too technical to be understood by the general public. Indeed, the rule had been suggested before the breakthrough result of Gkatzeils, Halpern, and Shah, but due to its complexity, researchers had been unable to show that it always produces a winner. Finding a simple algorithm to solve a complex problem is always satisfying, but in the case of a voting rule, which needs to be accepted by the public and politicians, it is an absolute necessity. Every voter should be able to understand how the winner is picked without any technical background.

Plurality veto

In our recent work [12], we presented a very simple voting rule, called plurality veto, achieving the optimal metric distortion of 3. The rule has two stages; the first of which is simply plurality voting—the most common rule in practice:

• (Plurality Stage) Each voter gives a single vote to their most favorite candidate. Thus, each candidate is initialized with a score equal to the number of voters who rank him at the top.

These scores are then gradually decreased in the second stage in which a candidate drops out of the race if his score reaches 0. Here’s how the scores are decreased:

• (Veto Stage) In an arbitrary order, each voter decrements the score of her least-favorite candidate among the standing ones. Thus, each voter gives a vote to one candidate in the first stage and takes back a vote from a typically different candidate in the second stage. Therefore, the score of each candidate reaches 0 at the end.

The winner is the last standing candidate (i.e., the candidate whose score reaches 0 last).

In plurality veto, the questions that voters are faced with are two of the most straightforward questions: most and least favorite candidates. As you can notice, the rule does not even require full rankings of voters. However, running the rule with these two questions comes with a trade-off: voters need to wait after the first stage for using their veto. Alternatively, we can also ask each voter to rank all candidates, and run the second stage instantly.

Here’s an example of how plurality veto picks a winner: (i) First, each voter sends a vote to their top choice, and thus, candidates a, b and c respectively start off with scores 1, 2 and 1. Let us now consider a run with the veto order red-purple-yellow-blue. (ii) The bottom choice of the red voter is c. Note that c gets eliminated because his score reaches 0. (iii) The next voter is the purple one whose bottom choice is also c. Since c already got eliminated, purple takes back a vote of candidate a instead since a is her next bottom choice. (iv) At this point, we know that candidate b will win because there is no other candidate left.

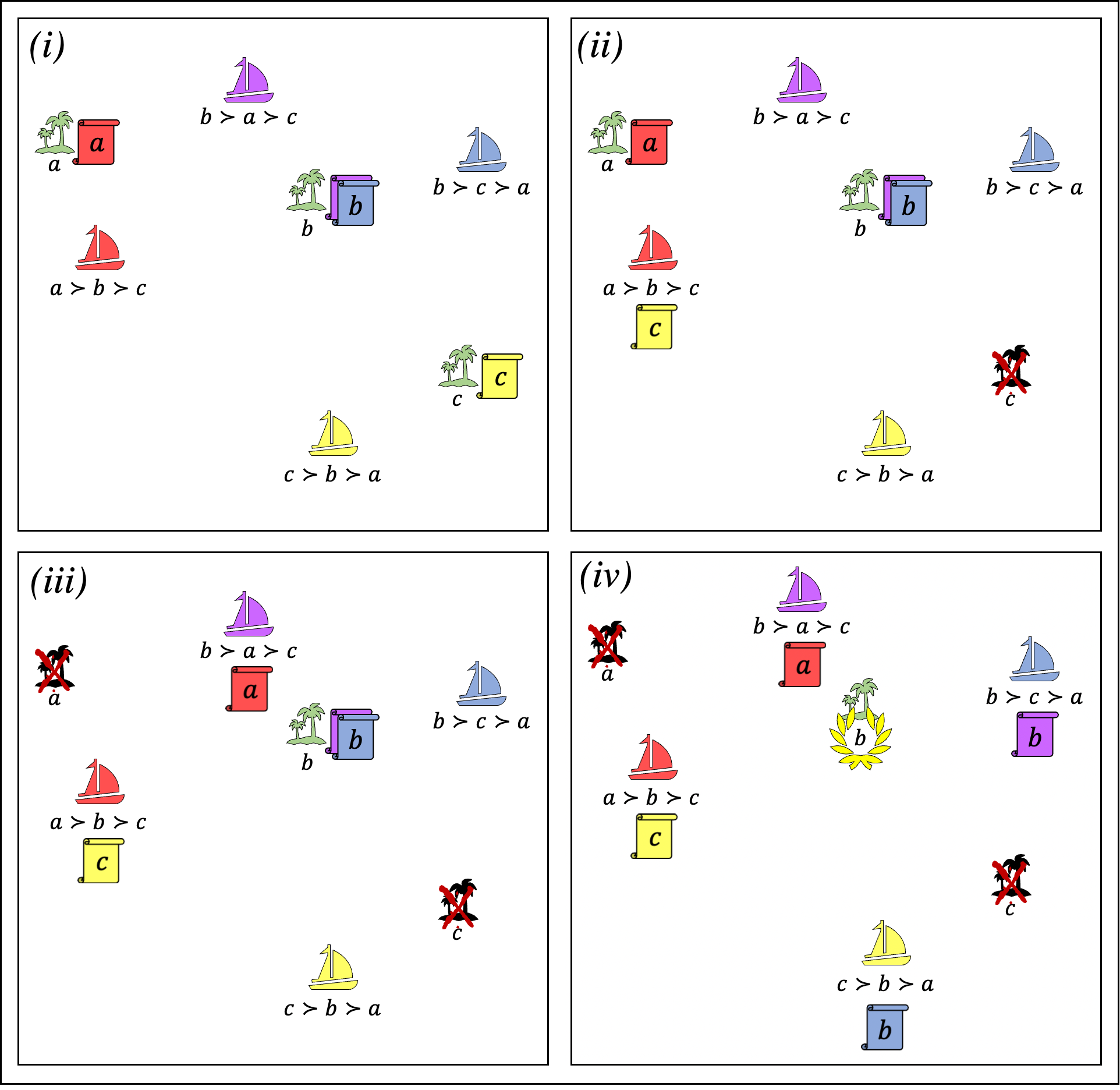
As can be seen from the example, plurality veto peels away “extreme” candidates, and thus, it ends up with central ones. Indeed, plurality veto always eliminates a candidate on the boundary of standing candidates in any (metric) space consistent with the rankings. On the other hand, the order in which the voters are processed may change the outcome as it also affects the elimination order. However, whichever order is used, it is guaranteed that we will end up with a candidate close to the center. This makes sense since there might be multiple candidates whose cost is at most 3 times larger than that of an optimal one, and as dictated by the lower bound of 3, it is not possible to distinguish between those candidates.

Future directions

The main drawback of plurality veto is that the outcome depends on the order in which voters are processed. On the other hand, this makes the structure of the set of possible winners (i.e. candidates who will win for at least one processing order of the voters) an interesting object to study. A closely related issue is that plurality veto (more generally, the metric distortion framework) is oblivious to ties. For example, the election above which gives the lower bound of 3 should be obviously declared a draw. However, since the framework does not acknowledge ties, we are forced to make arbitrary choices. Once we have a practical definition of ties, it might be possible to get rid of the arbitrariness of plurality veto. A quick workaround would be to declare all possible winners as ties but then we might end up with too many ties.

The metric distortion framework has led to numerous interesting questions and results, and offered a new perspective on voting and related topics. Interested readers may want to check out the following survey [13].

References

[1] Sneezing Dogs, Dancing Bees: How Animals Vote.
[2] Honeybee Democracy by Thomas Dyer Seeley, Princeton University Press, 2010.
[3] Voting: The wisdom of bees
[4] Communication Among Social Bees by Martin Lindauer, Harvard University Press, 1971.
[5] Elliot Anshelevich, Onkar Bhardwaj, and John Postl. Approximating optimal social choice under metric preferences. In Proc. 29th AAAI Conf. on Artificial Intelligence, pages 777–783, 2015.
[6] Elliot Anshelevich, Onkar Bhardwaj, Edith Elkind, John Postl, and Piotr Skowron. Approximating optimal social choice under metric preferences. Artificial Intelligence, 264:27–51, 2018.
[7] James M. Enelow and Melvin J. Hinich, The Spatial Theory of Voting, Cambridge Books, 1984.
[8] Piotr Skowron and Edith Elkind, Social Choice Under Metric Preferences: Scoring Rules and STV. Proceedings of the AAAI Conference on Artificial Intelligence, 31(1), 2017.
[9] David Kempe: An Analysis Framework for Metric Voting based on LP Duality. In Proc. of 2020 AAAI Conf. on Artificial Intelligence, New York, NY.
[10] Kamesh Munagala and Kangning Wang. Improved metric distortion for deterministic social choice rules. In Proc. 20th ACM Conf. on Economics and Computation, pages 245–262, 2019.
[11] Vasilis Gkatzelis, Daniel Halpern, and Nisarg Shah. Resolving the optimal metric distortion conjecture. In Proc. 61st IEEE Symp. on Foundations of Computer Science, pages 1427–1438, 2020.
[12] Fatih Erdem Kizilkaya and David Kempe, Plurality Veto: A Simple Voting Rule Achieving Optimal Metric Distortion. IJCAI, 2022.
[13] Elliot Anshelevich, Aris Filos-Ratsikas, Nisarg Shah, and Alexandros A. Voudouris. Distortion in social choice problems: The first 15 years and beyond. In Proc. 30th Intl. Joint Conf. on Artificial Intelligence, pages 4294–4301, 2021.

*For ease of presentation, we use female pronouns for voters and male pronouns for candidates throughout.

This work won a distinguished paper award at IJCAI-ECAI2022.

Fatih Erdem Kızılkaya is a PhD student in computer science at University of Southern California

Fatih Erdem Kızılkaya is a PhD student in computer science at University of Southern California