
ΑΙhub.org
Practical complexity of optimal play in games for two
It is a deep and dark December evening, but luckily Alice and Bob are not alone and can play the following fun game (after they have successfully exchanged cryptographic keys, of course). Alice picks a natural number m, and Bob attempts to pick another natural number n that is larger than m. This might not look like much of a game at first, but hold tight.
Of course, Bob can always win simply by choosing n to be m+1. In other words, he has a winning strategy. This winning strategy is a material proof of the statement “for each natural number m there exists a natural number n such that m<n.”
The correspondence between a game and a quantified logical proposition is not coincidental. Every 2-player game has a corresponding proposition that says one of the players has a winning strategy, and, vice versa, every quantified proposition can be turned into a game between two players.
We study reasoning power of various algorithms that decide games like these.
Of course we are not only interested in solving games: formally, we consider quantified formulas, which may encode games (even real ones like chess or tic-tac-toe), but also complex mathematical statements for which the truth value might even be unknown. We will always interpret them as 2-player games, though. And since we would like to solve these problems algorithmically, we concentrate on quantified Boolean formulas (QBF), which capture games with a finite number of states (technically, the example from the beginning is not finite, but consider a variation where n and m must have the same fixed number of bits: now there is only a finite number of possibilities, and, of course, it is now Alice who has a winning strategy).
A quantified Boolean formula is simply a logical proposition that formally describes the rules of the game. QBFs consist of Boolean (0-1) variables quantified either existentially or universally (this part is also called the prefix), and of a propositional formula over these variables that specifies which game positions (assignments of zeros and ones to the variables) are winning (this is called the matrix). The two players are existential and universal, and they each control the variables quantified accordingly. They take turns in the order in which the variables are quantified, and once all variables are set, the formula can be evaluated to determine the winner. Since there are no draws and only a finite number of rounds, one player must have a winning strategy; and it is our goal to determine which. A QBF is true if the existential player has a winning strategy, and is false in the other case.
The most common way to encode the matrix (i.e. the rules of the game) is in conjunctive normal form. This is effectively a listing of all positions winning for universal (known as clauses). The goal of existential is to avoid all of these clauses (by making sure at least one variable, possibly universal, in each clause is set differently), while universal strives to collect at least one (by ensuring all its variables are set as prescribed).
Solving QBFs is PSPACE-complete, which means very hard but at the same with a wide range of interesting applications, including formal verification of hardware and software and reactive synthesis of computer programs; and, of course, game modelling. State of the art in QBF solving includes several algorithms; in this paper we study Quantified Conflict-Driven Clause Learning (QCDCL).
The fundamental idea of QCDCL is to play out all possible branches of the game and recursively determine which positions are winning, all the way down to the initial position. On its own, this would take time proportional to 2 raised to the number of variables (i.e., the number of possible final positions). QCDCL improves on this naive approach in several ways (though it is still exponential in the worst case; indeed, we cannot hope for much more if we accept standard complexity assumptions like the Exponential Time Hypothesis).
Unsurprisingly, the main feature of QCDCL is the ability to learn new clauses. These learned clauses effectively compact existing knowledge about losing positions and identify new losing positions. If a position P is losing and another position Q leads to P by a forced move, then Q is also losing. If the game is lost, one can, by a chain of such inferences, eventually learn that the initial position is losing.
In general, QCDCL can learn about losing positions for both players. On false QBFs (games lost for existential), it is sufficient to learn clauses (positions lost for existential) only: eventually, one learns the empty clause, which says that the initial position is lost. In order to enable the same mechanism for true formulas (games winning for existential), one must additionally learn so-called cubes, which represent positions lost for universal. By an analogous process, one can derive from a true QBF the empty cube, which says the initial position is lost for universal.
In this paper, as is common in complexity studies of QBFs, we focus on false formulas, and we investigate whether using cube learning (which, recall, is not necessary in the case of false formulas) provides a speedup. We come to the surprising conclusion that even though cube learning “is for true formulas,” it can make QCDCL exponentially faster on false formulas as well.
Another add-on to QCDCL that we study is pure literal elimination (PLE), which in game language corresponds to elimination of Pareto dominated moves. Existential tries to reduce the number of remaining winning positions for universal with each move: a move that does not avoid any extra clauses is useless and the variable can safely be set to the other value. Similarly, universal tries to keep as many winning positions as possible, so a move that does not avoid any is a safe choice. In each case, the safely playable move is called a pure literal.
It stands to reason that elimination of pure literals should be beneficial, but we show that, surprisingly, this is not always the case.
In summary, we study 4 variants of QCDCL: with or without both cube learning and PLE. For each pair A, B of these algorithms, we determine their relationship as one of the three possibilities:
- A is always as fast as B (up to a polynomial factor) and sometimes exponentially faster;
- A is sometimes exponentially faster than B, but also B is sometimes exponentially faster than A;
- A and B are equally fast up to a polynomial factor.
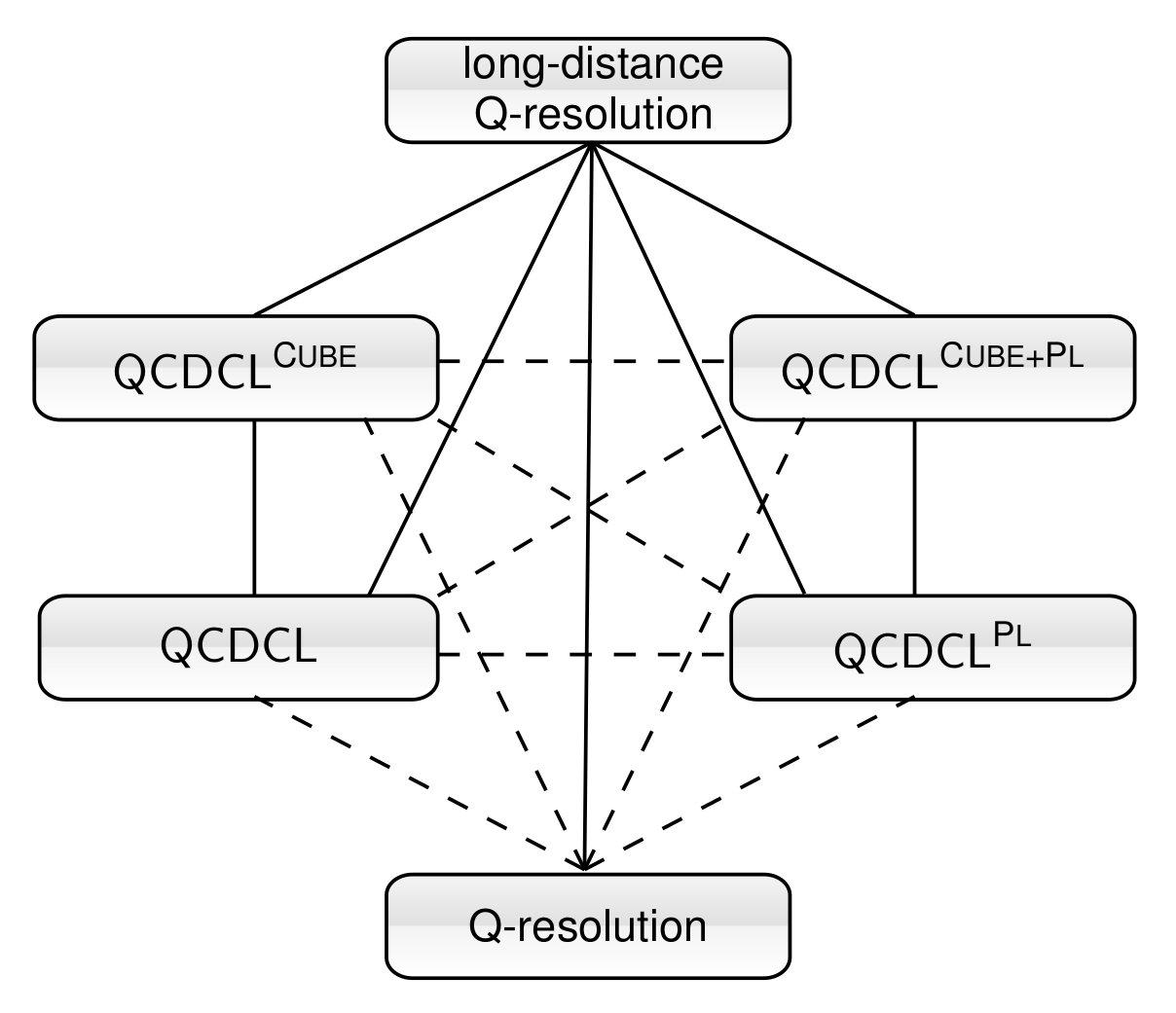
Technically, the way we show these results is by casting the algorithms as proof systems and applying tools from proof complexity. The learning that makes up the core of QCDCL can easily be shown to correspond to proofs in a simple proof system called long-distance Q-resolution (for clauses; for cubes it is commonly called long-distance Q-consensus). We show that adding cube learning always (irrespective of whether PLE is also used) leads to an exponential speedup, while proof systems with and without PLE are incomparable. PLE is also incomparable with cube learning when just one is used.
We complement our theoretical results with an experimental analysis with the QCDCL solver DepQBF, which supports all 4 variants of QCDCL. The experiments mostly match our theoretical findings, but there is an interesting twist. We observe that when PLE is supposed to be advantageous in theory, it is typically also advantageous in practice, but in contrast there are cases when cube learning is supposed to be advantageous and the practical results are mixed. This discrepancy between theory and practice is due to the fact that we analyze proof systems, which add non-determinism on top of QCDCL. There is little non-deterministic choice in eliminating pure literals, but learning cubes to one’s advantage might be more difficult without the power of non-determinism.
This work won a distinguished paper award at IJCAI 2022.
tags: IJCAI2022















