ΑΙhub.org
Understanding the impact of misspecification in inverse reinforcement learning
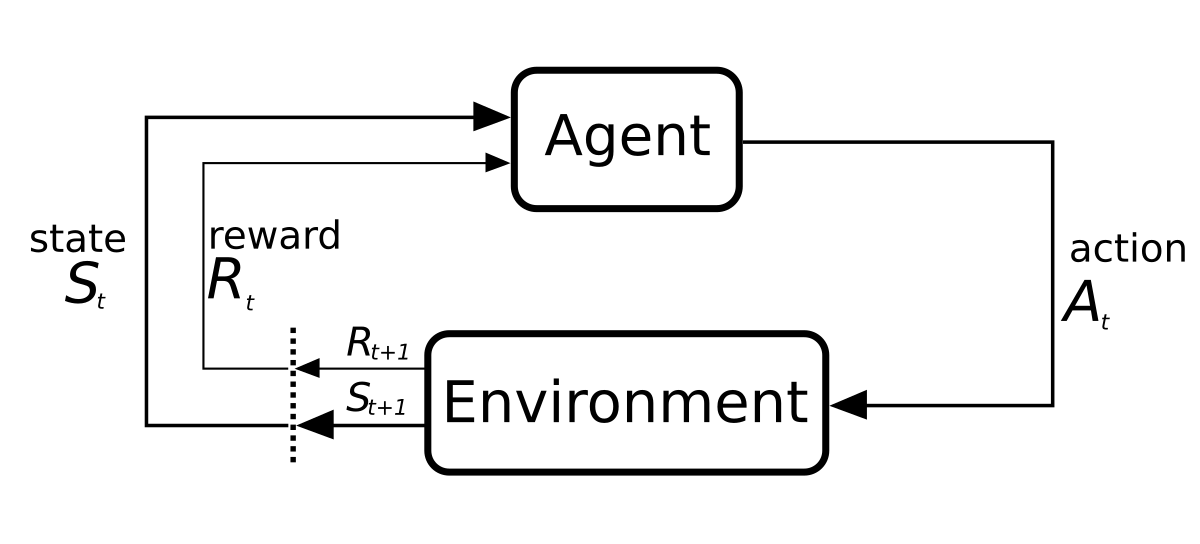Reinforcement learning diagram of a Markov decision process. EBatlleP, CC BY-SA 4.0.
In our recent AAAI 2023 paper, Misspecification in Inverse Reinforcement Learning (Skalse and Abate, 2023), we study the question of how robust the inverse reinforcement learning problem is to misspecification of the underlying behavioural model (namely, how the agent’s preferences relate to its behaviour). We provide a mathematical framework for reasoning about this question, and use that framework (based on equivalence classes and orders) to derive necessary and sufficient conditions describing what types of misspecification each of the standard behavioural models are (or are not) robust to. Moreover, we provide several results and formal tools, which can be used to study the misspecification robustness of any behavioural models that may be newly developed. Below, we will first explain the motivation for this work. Then, we will explain our results and, finally, describe ways to extend them.
What is inverse reinforcement learning?
Inverse reinforcement learning (IRL) is an area of machine learning concerned with inferring what objective an agent is pursuing, based on the actions taken by that agent. IRL is related to the notion of revealed preferences in psychology and economics, since it aims to infer preferences from behaviour. However, whereas current work on preference elicitation typically focuses on single-step decision problems, IRL instead considers the more general domain of sequential (multi-step) decision problems, over possibly large state spaces encompassing an environment or memory of the dynamics.
It is typically assumed that the behaviour of the observed agent is described by a (stationary) policy π, and that its objectives are described by a reward function, R. Therefore, the IRL problem can be formally stated as the problem of inferring a reward function R, based on a policy π which has been computed from R.
Why is inverse reinforcement learning interesting?
One of the central challenges in reinforcement learning is that, in real-world situations, it is typically very difficult to create reward functions that never incentivise undesirable behaviour. For example, suppose we wish to train a robot arm to safely grasp an object, or train a language model to always speak in a polite tone, etc. It is extremely difficult to write a reward function for these types of tasks, which can never be maximised in some unintended way.
One way to approach this problem is to use machine learning to learn a reward function from data, instead of specifying it manually. In particular, IRL could be used to learn a reward function for a task, based on demonstrations of what it looks like to solve that task correctly. In its most general form, it could be used as a self-supervised method for learning representations of human preferences based on raw observations of human behaviour.
There are also many other reasons to be interested in IRL. For example, IRL has been used as a tool for understanding animal behaviour (Yamaguchi et al. 2018). Moreover, all motivations for work on preference elicitation (such aiding public policy, or developing better commercial products, etc) also apply to IRL.
Why is misspecification central to inverse reinforcement learning?
In order to infer a reward function R from a policy π, we must make assumptions about how R relates to π. In other words, we must make assumptions about how a person’s preferences relate to their behaviour. We refer to this as the behavioural model. Of course, in the real world, this relationship can be incredibly complicated and thus difficult to precisely model. On the other hand, most IRL algorithms are based on one of three standard behavioural models: optimality, Boltzmann rationality, or causal entropy maximisation. These behavioural models are very simple, and essentially amount to assuming that π is noisily optimal. This means that the behavioural models that are typically used in practice will be misspecified in most situations. In fact, there are observable differences between human data and data synthesised using these standard assumptions (Orsini et al. 2021). This raises the concern that they might systematically lead to flawed inferences if applied to real-world data.
One response to this is to make behavioural models that are as accurate as possible. However, while a behavioural model can be more or less accurate, it will never be realistically possible to create a behavioural model that is completely free from misspecification (with the possible exception of certain very narrow domains). This means that, if we wish to use IRL as a tool for preference elicitation, then it is crucial to have an understanding of how robust the IRL problem is to misspecification of the behavioural model. Is it enough to have a behavioural model which is roughly accurate, or do we need to have a highly accurate behavioural model to ensure accurate inferences?
Our methodology
In our paper, we consider the setting where an IRL algorithm assumes that the observed policy is generated via a function f : R -> Π, but where it may in fact be generated via some other function, g : R -> Π (where R is the space of all reward functions, and Π is the space of all policies). We are then interested in deriving necessary and sufficient conditions on g, which ensure that the learnt reward function is “close enough” to the true reward function.
To do this, we must first formalise what it means for two reward functions to be “close enough”. We have chosen to do this in terms of equivalence relations. That is, we assume that we have an equivalence relation on R, and that the learnt reward function is “close enough” to the true reward function if they are both in the same equivalence class. We use two equivalence classes; the first says that two reward functions are equivalent if they have the same optimal policies, and the second says that they are equivalent if they have the same ordering of policies. The first condition should be sufficient, if we are able to compute optimal policies. The second condition is much stronger, but may be more appropriate in cases where we cannot necessarily compute an optimal policy (which is the case in most complex environments).
Given this formal setup, we then provide necessary and sufficient conditions describing what types of misspecification each of the three standard behavioural models (ie optimality, Boltzmann-rationality, and causal entropy maximisation) are (or are not) robust to, given both of the equivalence relations. Moreover, we provide several formal tools and auxiliary results, which can be used to easily derive the misspecification robustness of new behavioural models, beyond the three that we consider directly in our work.
Results and takeaways
We find that the optimality model is highly sensitive to misspecification, that the Boltzmann-rational model is robust to at least moderate misspecification, and that the maximal causal entropy model lies somewhere between the two. For each of these three models, we provide necessary and sufficient conditions, describing their robustness: for the exact formal statement, we refer to the main paper. These results can be used to determine whether or not a given IRL method is robustly applicable in a given situation.
Interestingly, we find that none of the standard behavioural models are robust to a misspecified discount factor, or to misspecification of the model dynamics. This is somewhat surprising, since the discount factor is often selected somewhat arbitrarily, and since it can be hard to establish after the fact which discount value was used. It is less surprising that the model dynamics must be specified correctly, but it is still important to have established this formally.
We also derive necessary-and-sufficient conditions describing when two reward functions induce the same policy ordering (i.e., when they have the same pairwise preferences between all policies). We expect this result to be valuable, independently of our other results.
Limitations and further work
There are several ways to extend our work. First of all, we have been working with equivalence relations, where two reward functions are either equivalent or not. It would be interesting to instead consider distance metrics on R, such as e.g. EPIC (Gleave et al, 2020). This could make it possible to obtain results such as bounds on the distance between the true reward function and the learnt reward function, given various forms of misspecification. Alternatively, we could also look for alternative interesting equivalence relations, besides the two we consider in this work.
We have studied the behaviour of algorithms in the limit of infinite data, under the assumption that this is similar to their behaviour in the case of finite but sufficiently large amounts of data. Therefore, another possible extension could be to more rigorously examine the properties of these models in the case of finite data.
Finally, our analysis primarily considers behavioural models that are currently most popular in the IRL literature. Another direction for extensions would be to broaden our analysis to larger classes of models. In particular, it would be interesting to analyse more realistic behavioural models, which incorporate e.g. prospect theory (Kahneman and Tversky 1979) or hyperbolic discounting.
References
J. Skalse and A. Abate, Misspecification in Inverse Reinforcement Learning, 37th AAAI Conference on Artificial Intelligence (AAAI), 2023.
Gleave, A.; Dennis, M. D.; Legg, S.; Russell, S.; and Leike, J. Quantifying Differences in Reward Functions. In International Conference on Learning Representations, 2021.
Kahneman, D.; and Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica, 1979.
Orsini, M.; Raichuk, A.; Hussenot, L.; Vincent, D.; Dadashi, R.; Girgin, S.; Geist, M.; Bachem, O.; Pietquin, O.; and Andrychowicz, M. What Matters for Adversarial Imitation Learning? Proceedings of the 35th International Conference on Neural Information Processing Systems, 2021
Yamaguchi, S.; Naoki, H.; Ikeda, M.; Tsukada, Y.; Nakano, S.; Mori, I.; and Ishii, S. Identification of animal behavioral strategies by inverse reinforcement learning. PLOS Computational Biology, 2018.
This work won the AAAI-23 outstanding paper award.
tags: AAAI, AAAI2023
AIhub is supported by:
