The Kidney Exchange Problem: Interview with Úrsula Hébert-Johnson, Chinmay Sonar and Vaishali Surianarayanan

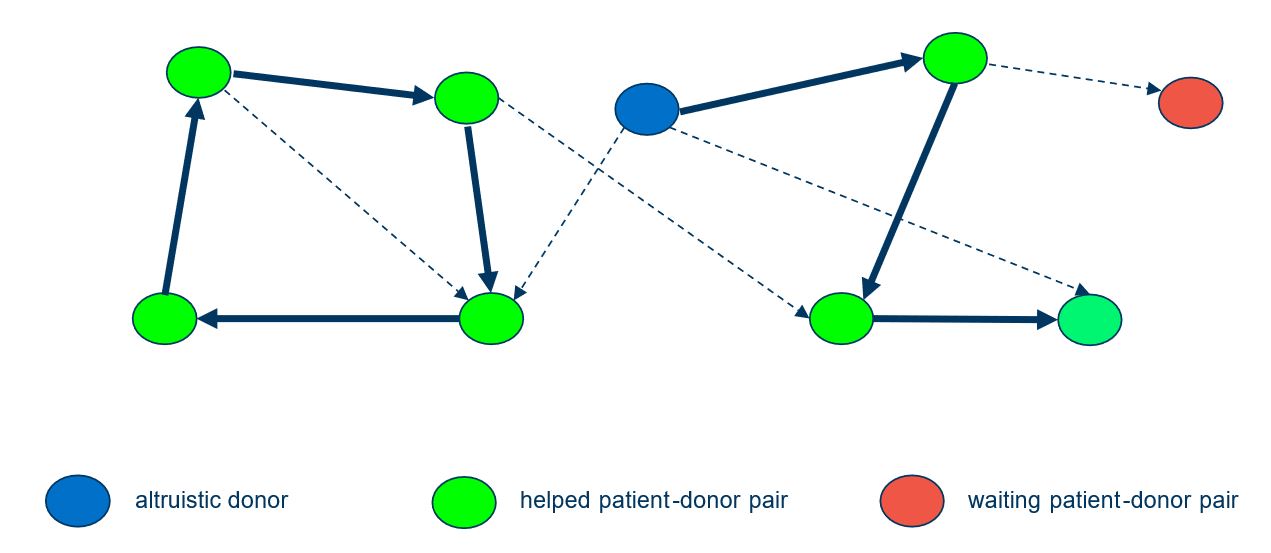An example assignment with a cycle and a path maximizing the number of patients helped.

In their work Parameterized Complexity of Kidney Exchange Revisited, presented at IJCAI 2024, Úrsula Hébert-Johnson, Daniel Lokshtanov, Chinmay Sonar and Vaishali Surianarayanan consider the Kidney Exchange Problem. We hear from Úrsula, Chinmay and Vaishali about kidney exchange, and how they went about solving two of the open problems in this field.

What is the topic of your paper, and why is it such a vital area for study?

Kidney disease affects tens of thousands of patients in the United States and hundreds of millions across the world. One way to treat kidney failure is to regularly undergo dialysis. But going to regular appointments for years is difficult, especially for the elderly. Another treatment option is to get a kidney transplant by joining a waiting list to be matched with a compatible donor. Unfortunately, the demand for kidney donations far exceeds the number of transplants available. Currently, the median waiting time for a kidney transplant (from a deceased donor) is 4.05 years in the U.S., and many patients fail to ever find a match.

Patients often have a friend or family member who is willing to donate a kidney; however, that donor’s kidney type might not be compatible. In 2000, Kidney Paired Donation (KPD) was introduced to address this issue and increase the number of patients who receive a transplant. KPD is a centrally administered barter-exchange market for kidney donations. A patient with an incompatible donor can participate in the market in the hope of exchanging their donor with a compatible donor from another participating pair. The popularity of KPD has grown over the years, and it now operates in several countries including the United States, the United Kingdom, the Netherlands, and India. KPD leads to a natural optimization problem known as the Kidney Exchange Problem, in which the goal is to maximize the number of patients who receive a transplant. In our paper, we give two algorithms that solve this problem efficiently and study its computational complexity.

Could you give us a bit of background to the Kidney Exchange Problem – how does the method work in general?

To understand the Kidney Exchange Problem, let’s consider a compatibility graph where each node is either a patient-donor pair or a single donor (to allow for altruistic donors), and the edges between the nodes denote compatibility, i.e., a directed edge from node X pointing to node Y denotes that the patient at node Y can receive a kidney from the donor at node X. A cycle in this graph gives a possible way of performing kidney exchanges in which the patient at each node in the cycle gets a compatible kidney from the donor at the previous node. The other option is to find a path starting from an altruistic donor: in this case, each donor donates his/her kidney to the next pair along the path. The way to help the maximum number of patients is to find a set of non-overlapping cycles and paths which together include the maximum number of patients.

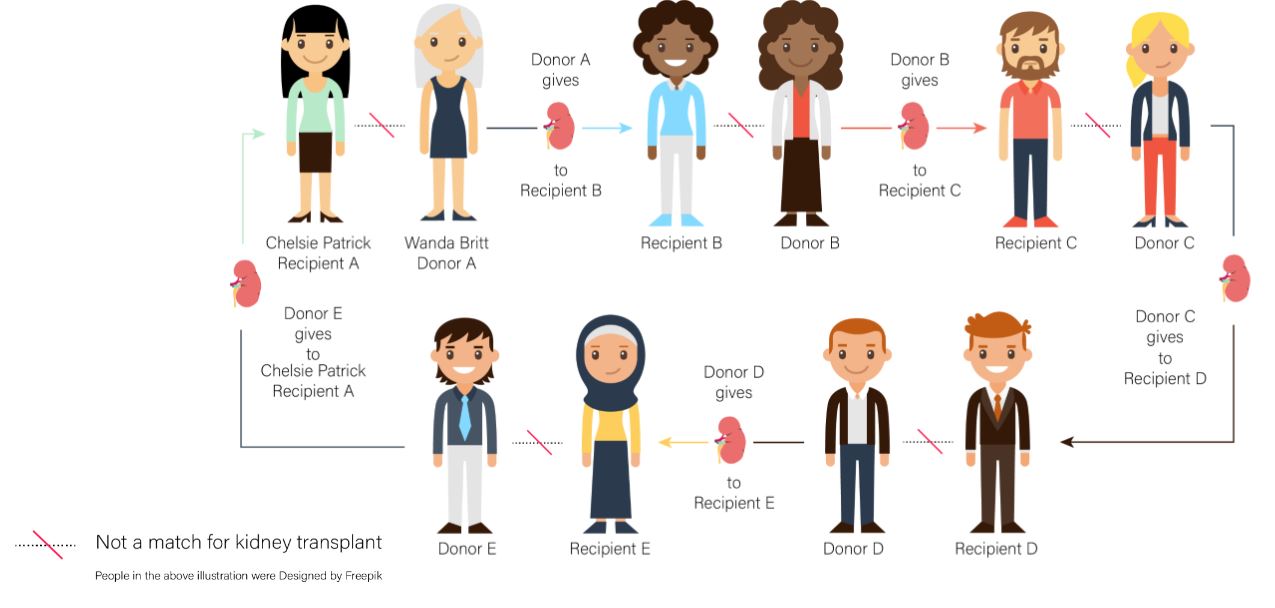An example of a kidney exchange cycle. Image credit: UNC School of Medicine.

An example assignment with a cycle and a path maximizing the number of patients helped.

Since KPD is a barter system, the transplants for all the patients on a cycle or path need to be performed simultaneously; otherwise, a donor is not obligated to donate his/her kidney if the paired patient has already received one. This constraint requires us to choose relatively small cycles and paths in the final assignment.

KPD is overseen by health organizations in each participating country. For example, for the United States National Kidney Registry, UCSF health and UCLA health offer a kidney exchange program. As the number of patients/donors increases, finding assignments of donors to patients becomes computationally hard (i.e., it can take a long time to find an optimal set of cycles and paths). To overcome this issue, researchers have mainly tried two different directions: One is to find an approximately optimal assignment (i.e., an assignment that does not help as many patients as the optimal but can be computed quickly), and the other approach is to understand structural properties of the compatibility graph to design algorithms that are efficient in certain cases. We take the second approach.

What are the main contributions of your paper?

The algorithms in our paper are parameterized algorithms, which means that the running times are fast when certain parameters are small. Since the Kidney Exchange Problem is NP-hard (meaning there is unlikely to be an efficient, polynomial-time algorithm that works in all cases), this problem is a great candidate for parameterized algorithms.

We present two algorithms in our paper, the first of which is pretty easy to state. For this one, the parameter is the number of patients who receive a kidney donation, so this algorithm can be used when the number of patients we expect to help is relatively small. For this case, we designed an efficient algorithm that given t, either finds donors for at least t patients, or determines that such a solution does not exist. The running time is roughly 4^t, which means this algorithm runs fast when t is small, even though the running time is exponential in general.

For our second algorithm, we assume the number of “kidney types” is relatively small. To see what this means, imagine that two kidney donors (or patients), Kirk and Kendra, have the same blood type, age, and other medical characteristics. If all of their relevant characteristics are the same, then the set of patients (or donors) that Kirk and Kendra are compatible with will be the same. This means Kirk and Kendra have the same “kidney type.” Our second algorithm runs efficiently when the number of distinct kidney types is small. The running time is a double exponential function of the number of kidney types, so in some sense this is slower than the first algorithm. The advantage of this approach, however, is that the number of kidney types is more likely to be small in the real world. The number of patients we wish to help will often be large, but the number of blood types, etc., can indeed be a small constant.

Looking at the open problems (from previous work) that you’ve resolved, could you talk a bit about your methodology? How did you go about solving these problems?

Before our paper, there was already a known fixed parameter-tractable (FPT) algorithm for the Kidney Exchange Problem, in the case where the parameter is the number of patients t who receive a kidney. The running time of that algorithm was roughly 161^t, so our 4^t algorithm significantly improves upon that. To say a bit about our methods, our algorithm uses algebraic techniques. We expressed each possible solution as a term in a polynomial, and we used properties of a related group ring to check whether a solution exists.

For the case when the parameter is the number of kidney types, we resolved the open problem of whether there is an FPT algorithm for the Kidney Exchange Problem in this scenario. For this algorithm, we formulated the problem as an integer linear program (ILP) that can be solved in FPT time, parameterized by the number of variables.

Are there other open problems that you’d like to tackle next?

A natural next step from our research is to improve the running times of our algorithms. Another promising avenue is to apply the structural insights from our parameterized algorithms to develop heuristics that perform well on real-world data.

Some earlier algorithms have successfully bridged the gap between theory and practice and are currently used to power kidney exchange programs across the U.S. Notably, one of the researchers behind these algorithms received the AAAI 2023 Award for AI for the Benefit of Humanity. Inspired by this, we are motivated to further advance research in this important area.

This research was also presented by Vaishali in the UCSB Grad Slam Finals, where students deliver a 3-minute elevator pitch on their work. You can watch the recording below:

About the authors

	Úrsula Hébert-Johnson is a PhD student in the computer science department at UC Santa Barbara, advised by Daniel Lokshtanov. Her research revolves around parameterized graph algorithms and polynomial-time graph counting and sampling algorithms. She is particularly interested in graph algorithms that use algebraic techniques, such as the ring of polynomials that can be used to describe solutions to the Kidney Exchange Problem. Prior to UCSB, she received her bachelor’s degree in mathematics at Stanford University.
	Chinmay Sonar is a Machine Learning Scientist at Visa. His work focuses on developing generative AI models for video question-answering tasks and real-time payment (RTP) fraud detection systems. His recent research has been published in EMNLP, IJCAI, and ESA. Previously, he has also worked on resource allocation problems within the broader field of AI, including kidney paired donation, facility location/clustering, and multi-winner elections. He recently completed his PhD in computer science from the University of California, Santa Barbara. He also holds a bachelor’s degree and a master’s degree from the Indian Institute of Technology (IIT) Gandhinagar.
	Vaishali Surianarayanan is a senior PhD candidate in the CS theory lab at UC Santa Barbara. Her research focuses on using parameterization for designing algorithms both in theory and practice for graph problems arising from various domains. She is also interested in databases and distributed systems and has pursued various research and industry internships in this domain. Her work has been published in top-tier AI and CS theory conferences like FOCS, SODA, and IJCAI. Outside of research, she loves to teach and is an active advocate of diversity, equity, and inclusion in tech. In her free time, she can often be found with her sketchbook.

Lucy Smith , Managing Editor for AIhub.

Lucy Smith , Managing Editor for AIhub.