Improving calibration by relating focal loss, temperature scaling, and properness

In machine learning classification tasks, achieving high accuracy is only part of the goal; it’s equally important for models to express how confident they are in their predictions – a concept known as model calibration. Well-calibrated models provide probability estimates that closely reflect the true likelihood of outcomes, which is critical in domains like healthcare, finance, and autonomous systems, where decision-making relies on trustworthy predictions. A key factor influencing both the accuracy and calibration of a model is the choice of the loss function during training. The loss function guides the model on how to learn from data by penalizing errors in prediction in a certain way. In this blog post, we will explore how to choose a loss function to achieve good calibration, focusing on the recently proposed focal loss and trying to understand why it leads to quite well-calibrated performance.

For multiclass classification problems, commonly used losses include cross-entropy (log-loss) and mean squared error (Brier score). These loss functions are strictly proper, meaning they are uniquely minimized when the predicted probabilities exactly match the ground truth probabilities. To illustrate properness, consider a training set where 10 instances have identical feature values, with 8 being actual positives and 2 negatives. When predicting the probability of a positive outcome for a new instance with the same features, it is logical to predict 0.8, and that’s precisely what proper losses incentivize the model to predict.

In practice, models trained with strictly proper losses such as cross-entropy and Brier score are indeed well-calibrated, but on the training set. When evaluating their performance on the test set, these models are often overconfident. This means that the predicted probabilities are systematically higher than the true likelihoods; the model assigns excessive confidence to its predictions, potentially resulting in misguided decisions based on these inflated probabilities.

A common approach to reducing overconfidence in a model’s predictions on a test set is to apply post-hoc calibration. This involves learning a transformation on a validation set that adjusts the model’s predicted probabilities to better align with true probabilities without altering the model itself.

Temperature scaling is one of the simplest post-hoc calibration methods. It introduces a single scalar parameter called the temperature that scales the logits (pre-softmax outputs) before applying the softmax function to obtain probabilities. The temperature is learned by minimizing some loss (typically a proper loss such as cross-entropy) of the scaled predictions on the validation set.

Some loss functions can inherently produce quite well-calibrated performance on the test set without applying additional calibration methods. One such example is focal loss, which, despite not being a strictly proper loss function, has been observed to yield relatively well-calibrated probability estimates in practice. Understanding the reasons behind this phenomenon was a primary motivation for our research.

The focal loss, which incorporates a single non-negative hyperparameter , has the following expression:

(1)  

Here, the term is identical to cross-entropy loss expression, while the multiplicative term reduces the loss contribution from easy examples (those the model predicts correctly with high confidence) while putting more focus on difficult, misclassified instances. The argument denotes the model’s predicted probability scalar for the true class label.

In our paper, we showed that focal loss could be deconstructed into the composition of a proper loss and a confidence-raising transformation such that:

(2)  

Here, represents the whole predicted probability vector. We will refer to as the focal calibration map. We showed that is fixed (depends only on parameter) and confidence-raising transformation. By confidence-raising, we mean that the highest probability in the predicted vector is mapped to an even higher value.

We visualized the proper part of the focal loss and focal calibration map in the following visualization:

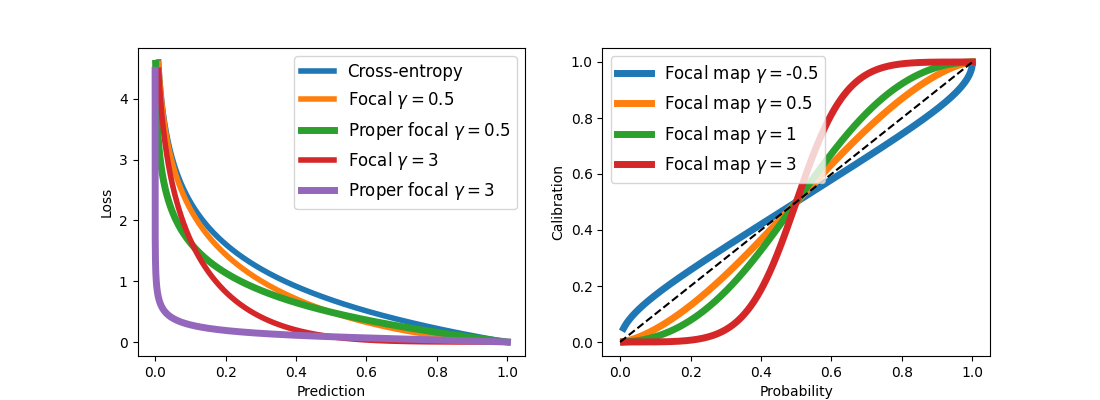Figure 1: Proper part of the focal loss and focal calibration map

We could note that the proper part of the focal loss is much steeper than both focal and cross-entropy losses. Also, technically, negative values result in valid but not-so-meaningful expressions.

In the binary case, the focal calibration map has the following expression:

(3)  

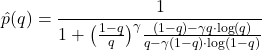
Surprisingly, this expression, when applied to the logit before the sigmoid step , is very close to temperature scaling transformation:

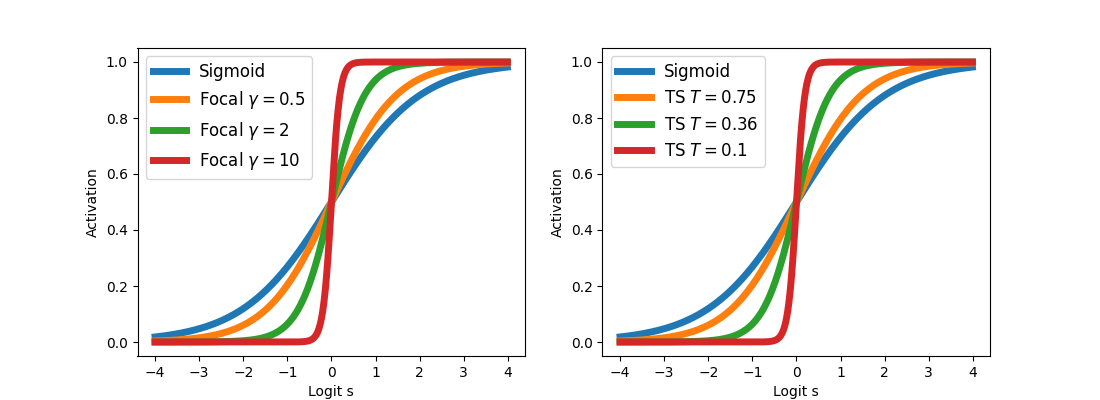Figure 2: Focal calibration and temperature scaling comparison

Moreover, we showed that these two transformations are not identical, but the focal calibration map with parameter could be lower and upper bounded with two temperature scaling with parameters and .

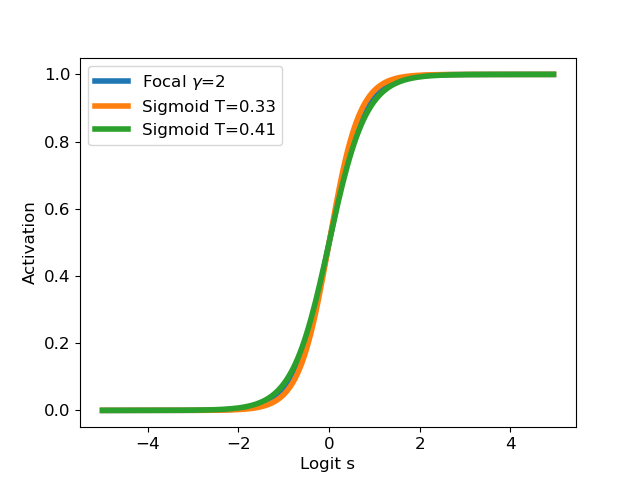Figure 3: Focal calibration (with respect to logit before sigmoid step) bounded between two temperature scaling transformations

We believe that the focal loss decomposition into proper loss and confidence-raising calibration map could explain its well-calibrated performance on the test set.
Models trained with proper losses typically achieve good calibration on the training set but tend to be overconfident on the test set, and we could expect similar performance for the proper part of the focal loss (with respect to probabilities after focal calibration). However, by examining the predicted probabilities before applying the confidence-raising transformation, we might expect slightly underconfident probabilities on the training set and more well-calibrated outcomes on the test set.

In the multiclass setting, focal calibration and temperature scaling are related but not as closely as in the binary case. To leverage the calibration properties of both transformations, we propose combining them into a new calibration technique called focal temperature scaling. This approach involves tuning two parameters – the temperature and the focal parameter – to balance overconfidence and underconfidence in the model’s predictions. By optimizing these parameters on the validation set, we aim to achieve improved calibration performance.

The experiments performed on CIFAR-10, 100, and TinyImageNet suggest that focal temperature scaling clearly outperforms standard temperature scaling and could be combined on top of other calibration methods, such as AdaFocal, to potentially enhance calibration even further.

Summary

1. We showed how the decomposition of a focal loss into proper loss and confidence-raising map could explain its well-calibration on the test set.
2. We showed the surprising connection of the focal calibration map with temperature scaling, especially in the binary cases.
3. We highlighted how composing this confidence-raising map with temperature scaling could improve model calibration.

This work was accepted at ECAI 2024. Read the paper in full:

• Improving Calibration by Relating Focal Loss, Temperature Scaling, and Properness, Viacheslav Komisarenko, Meelis Kull

Viacheslav Komisarenko is a PhD student at the University of Tartu

Viacheslav Komisarenko is a PhD student at the University of Tartu