
ΑΙhub.org
Physics-constrained deep learning of building thermal dynamics
Energy-efficient buildings are one of the top priorities to sustainably address the global energy demands and reduction of CO2 emissions. Advanced control strategies for buildings have been identified as a potential solution with projected energy saving potential of up to 28%. However, the main bottleneck of the model-free methods such as reinforcement learning (RL) is the sampling inefficiency and thus requirement for large datasets, which are costly to obtain or often not available in the engineering practice. On the other hand, model-based methods such as model predictive control (MPC) suffer from large cost associated with the development of the physics-based building thermal dynamics model.

We address the challenge of developing cost and data-efficient predictive models of a building’s thermal dynamics via physics-constrained deep learning. We show that with the proposed methodology, we can greatly decrease the required modeling expertise by systematically encoding structural assumptions and constraints while achieving a state-of-the-art modeling performance. One of the main advantages is the generality of the proposed neural architecture, which represents a generic abstraction applicable to an arbitrary building.
Methodology
In general, building thermal behavior is determined by high-dimensional, nonlinear, and often discontinuous dynamical processes. Thus, obtaining accurate and reliable dynamical models of buildings remains a challenging task and typically involves computationally demanding physics-based modeling. As a consequence, high computational demands and non-differentiability can easily cast the physics-based model unsuitable for efficient gradient-based optimization required in various applications. Therefore, a sound trade-off between the model accuracy and simplicity is required.
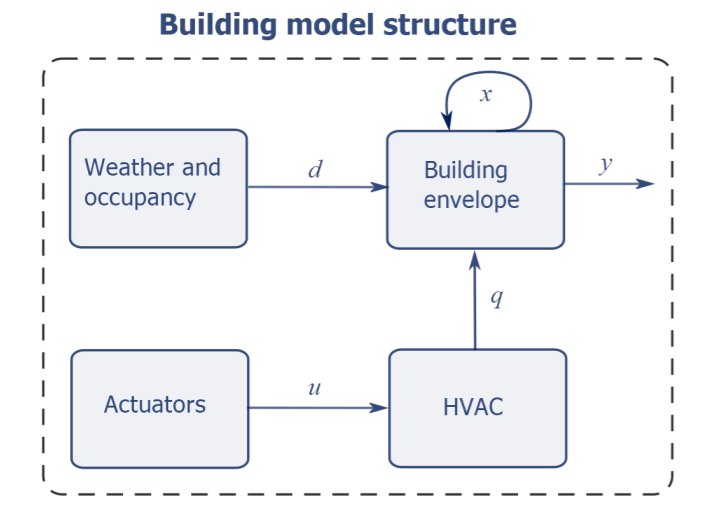
The nature of the building’s dynamics allows us to represent every building as a computational graph, shown in Figure 1(a). Every building consists of a building envelope determining the rate of heat transfer within the building structure and internal air temperature, heating ventilation and air conditioning (HVAC) components supplying the building with heat and fresh air, and disturbances such as the influence of the weather and occupancy. Now, instead of discarding all of this prior knowledge as is done in black-box modeling, we incorporate the generic physics directly into deep neural networks to improve their prediction accuracy and generalization from small datasets. To incorporate physics-based constraints and structural assumptions, we introduce a generic block nonlinear state space model (SSM).
Each neural block of this structured graph model, shown in Figure 1(b), corresponds to a different part of the generic building model structure from Figure 1(b). In particular, fx models building envelope, fu represents HVAC dynamics, fd captures the effect of weather disturbances, fy represents sensor placement, and fo estimates the current temperatures of the building envelope from the past measurements.
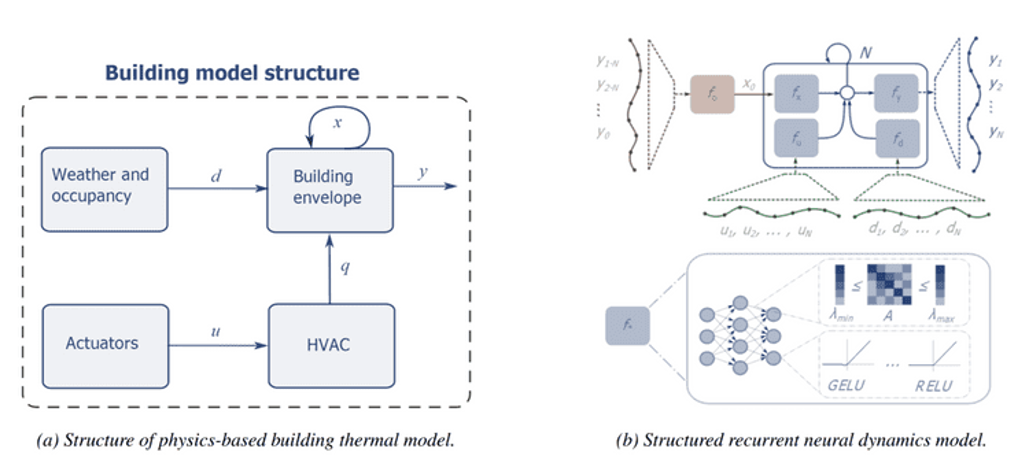
Figure 1: Generic structure of physics-inspired recurrent neural dynamics model architecture. Weights of individual neural blocks f∗ are parametrized by linear maps with constrained eigenvalues, while component outputs are subject to penalty constraints parametrized by common activation functions.
An important physics insight is that building thermal dynamics represents a dissipative system. The system’s dissipativity is physically interpreted as heat losses of the building envelope, which are influenced by numerous factors such as building topology, material properties, insulation levels, or window-to-wall ratio. These parameters determine the overall heat transfer coefficient of the building, called U-values, where smaller U-values mean better insulation. The problem is that obtaining accurate information about the parameters required for estimation of the U-values from technical sheets is a time consuming and tedious task. From a dynamical perspective, U-values can be related to the system eigenvalues. This inspired us to enforce physically reasonable constraints on the eigenvalues of a model’s weight matrices as illustrated in Figure 1(b).
Additionally, with the optimization strategy known as the penalty method, we can add further constraints to our model such that its variables remain within physically realistic bounds. Thanks to the block-structured dynamics, we can now constrain the dynamical contribution of inputs fu and disturbances fd towards the overall dynamics via additional terms in the loss function. This allows us to limit the effect of the external factors to be bounded within physically plausible ranges. For instance, it is not physically realistic that 1 K change in the ambient temperature would cause a 2 K change in indoor temperature in a single time step. Therefore, we structure and constrain our deep learning model such that it respects these physical constraints.
Experiments using real-world dataset
Now we will demonstrate that our physics-constrained deep learning model can learn an accurate and generalizable representation of complex dynamics of a large-scale commercial office building, given only a limited amount of data.
The building used in this study is a commercial office building with 20 thermal zones. Heating and cooling are provided by a variable air volume (VAV) system served by 44 air handling units (AHUs) serving 24 VAV boxes (zones). Each VAV box is equipped with a hot water reheat coil. A boiler, fed by natural gas, supplies hot water to the reheat coils and AHU coils. Chilled water is supplied by a central chiller plant. The time-series dataset consists of 30 days, which corresponds to only 2880 datapoints. We group the dataset into evenly split training, development, and test sets, 960 data points each. Further details on experiment setup can be found in the paper.
We perform dynamical simulation of the learned dynamical model by unrolling its dynamics into the future. By comparing predicted trajectories (blue) against measured data (red) as shown in Figure 2, we demonstrate the capability to generalize complex dynamics over 30-days using only 10-days of training data.
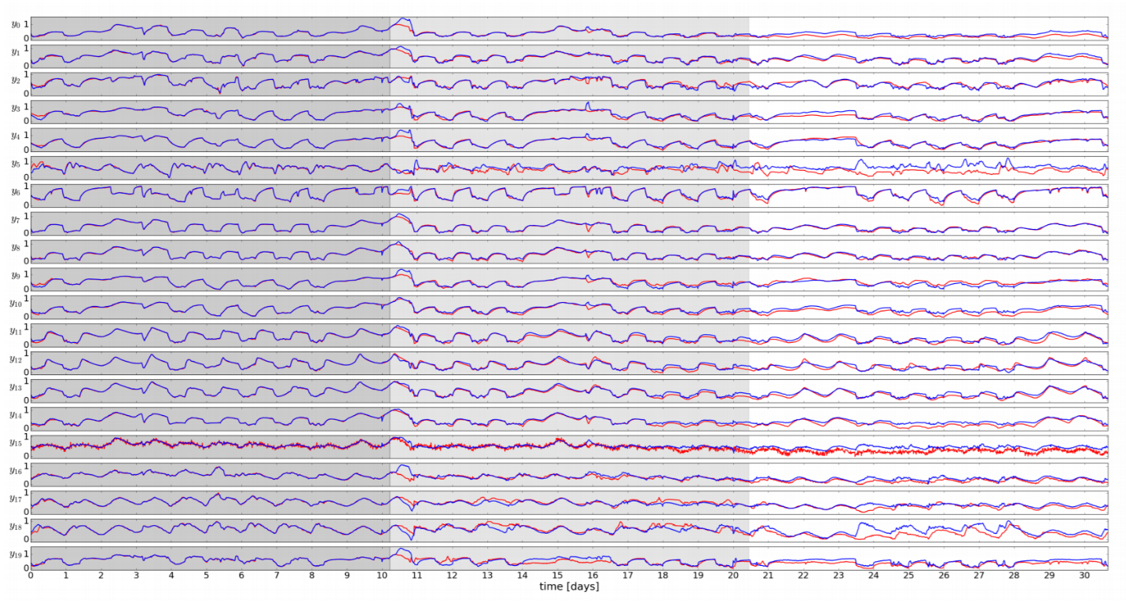
Figure 2: Open-loop trajectories of the learned (blue) and ground truth (red) multi-zone building thermal dynamics.
Now we assess the simulated open-loop and N-step mean squared error (MSE) performance of the recurrent model with and without physics-constraints and structure. The MSE metrics are shown in Figure 3. The open-loop MSE of the best-performing constrained and structured model corresponds to 0.49 K. In comparison, the gray-box system identification methods trained on a similar amount of data reports open-loop MSE roughly equal to 1.00 K. Hence our preliminary results show more than 50% reduction in error against state-of-the-art in the literature.
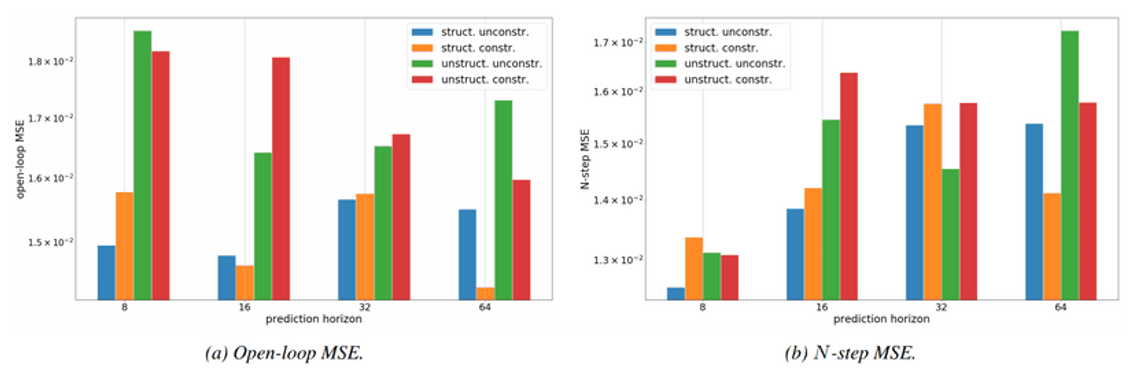
Figure 3: Effect of penalty constraints on open-loop and N-step ahead MSE evaluated on a test set using structured and unstructured models, with increasing training prediction horizon N.
Conclusions
Reliable data-driven methods that are cost-effective in terms of computational demands, data collection, and domain expertise have the potential to revolutionize the field of energy-efficient building operations through the wide-scale acquisition of building specific, scalable, and accurate prediction models. We presented a constrained deep learning method for sample-efficient and physics-consistent data-driven modeling of building thermal dynamics. Our approach does not require the large time investments by domain experts and extensive computational resources demanded by physics-based emulator models. Based on only 10 days’ measurements, we significantly improve on prior state-of-the-art results for a modeling task using a real-world large-scale office building dataset. The presented method represents a promising modeling paradigm for advanced predictive control strategies for energy-efficient operations in real-world buildings. More generally, our proposed method is a promising modeling paradigm for advanced predictive control strategies for energy-efficient operations in real-world buildings and beyond.
This article summarizes work presented at the NeurIPS 2020 Workshop Tackling Climate Change with Machine Learning:
Physics-constrained Deep Recurrent Neural Models of Building Thermal Dynamics, Jan Drgoňa, Aaron R. Tuor, Vikas Chandan, Draguna L. Vrabie.
Find out more about the work here.
tags: Focus on climate action, Focus on UN SDGs

















