
ΑΙhub.org
CMU-MATH team’s innovative approach secures 2nd place at the AIMO prize

By Yangzhen Wu, Zhiqing Sun, Shanda Li, Sean Welleck, Yiming Yang
Recently, our CMU-MATH team proudly clinched 2nd place in the Artificial Intelligence Mathematical Olympiad (AIMO) out of 1,161 participating teams, earning a prize of ![]() ! This prestigious competition aims to revolutionize AI in mathematical problem-solving, with the ultimate goal of building a publicly-shared AI model capable of winning a gold medal in the International Mathematical Olympiad (IMO). Dive into our blog to discover the winning formula that set us apart in this significant contest.
! This prestigious competition aims to revolutionize AI in mathematical problem-solving, with the ultimate goal of building a publicly-shared AI model capable of winning a gold medal in the International Mathematical Olympiad (IMO). Dive into our blog to discover the winning formula that set us apart in this significant contest.
Background: The AIMO competition
The Artificial Intelligence Mathematical Olympiad (AIMO) Prize, initiated by XTX Markets, is a pioneering competition designed to revolutionize AI’s role in mathematical problem-solving. It pushes the boundaries of AI by solving complex mathematical problems akin to those in the International Mathematical Olympiad (IMO). The advisory committee of AIMO includes Timothy Gowers and Terence Tao, both winners of the Fields Medal. Attracting attention from world-class mathematicians as well as machine learning researchers, the AIMO sets a new benchmark for excellence in the field.
AIMO has introduced a series of progress prizes. The first of these was a Kaggle competition, with the 50 test problems hidden from competitors. The problems are comparable in difficulty to the AMC12 and AIME exams for the USA IMO team pre-selection. The private leaderboard determined the final rankings, which then determined the distribution of ![]() in the one-million dollar prize pool among the top five teams. Each submitted solution was allocated either a P100 GPU or 2xT4 GPUs, with up to 9 hours to solve the 50 problems.
in the one-million dollar prize pool among the top five teams. Each submitted solution was allocated either a P100 GPU or 2xT4 GPUs, with up to 9 hours to solve the 50 problems.
Just to give an idea about how the problems look like, AIMO provided a 10-problem training set open to the public. Here are two example problems in the set:
- Let
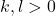 be parameters. The parabola
be parameters. The parabola 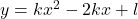 intersects the line
intersects the line 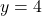 at two points
at two points 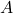 and
and 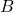 . These points are distance 6 apart. What is the sum of the squares of the distances from
. These points are distance 6 apart. What is the sum of the squares of the distances from 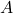 and
and 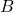 to the origin?
to the origin?
- Each of the three-digits numbers
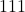 to
to 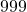 is coloured blue or yellow in such a way that the sum of any two (not necessarily different) yellow numbers is equal to a blue number. What is the maximum possible number of yellow numbers there can be?
is coloured blue or yellow in such a way that the sum of any two (not necessarily different) yellow numbers is equal to a blue number. What is the maximum possible number of yellow numbers there can be?
The first problem is about analytic geometry. It requires the model to understand geometric objects based on textual descriptions and perform symbolic computations using the distance formula and Vieta’s formulas. The second problem falls under extremal combinatorics, a topic beyond the scope of high school math. It’s notoriously challenging because there’s no general formula to apply; solving it requires creative thinking to exploit the problem’s structure. It’s non-trivial to master all these required capabilities even for humans, let alone language models.
In general, the problems in AIMO were significantly more challenging than those in GSM8K, a standard mathematical reasoning benchmark for LLMs, and about as difficult as the hardest problems in the challenging MATH dataset. The limited computational resources—P100 and T4 GPUs, both over five years old and much slower than more advanced hardware—posed an additional challenge. Thus, it was crucial to employ appropriate models and inference strategies to maximize accuracy within the constraints of limited memory and FLOPs.
Our winning formula
Unlike most teams that relied on a single model for the competition, we utilized a dual-model approach. Our final solutions were derived through a weighted majority voting system, which consists of generating multiple solutions with a policy model, assigning a weight to each solution using a reward model, and then choosing the answer with the highest total weight. Specifically, we paired a policy model—designed to generate problem solutions in the form of computer code—with a reward model—which scored the outputs of the policy model. Our final solutions were derived through a weighted majority voting system, where the answers were generated by the policy model and the weights were determined by the scores from the reward model. This strategy stemmed from our study on compute-optimal inference, demonstrating that weighted majority voting with a reward model consistently outperforms naive majority voting given the same inference budget.
Both models in our submission were fine-tuned from the DeepSeek-Math-7B-RL checkpoint. Below, we detail the fine-tuning process and inference strategies for each model.
Policy model: Program-aided problem solver based on self-refinement
The policy model served as the primary problem solver in our approach. We noted that LLMs can perform mathematical reasoning using both text and programs. Natural language excels in abstract reasoning but falls short in precise computation, symbolic manipulation, and algorithmic processing. Programs, on the other hand, are adept at rigorous operations and can leverage specialized tools like equation solvers for complex calculations. To harness the benefits of both methods, we implemented the Program-Aided Language Models (PAL) or more precisely Tool-Augmented Reasoning (ToRA) approach, originally proposed by CMU & Microsoft. This approach combines natural language reasoning with program-based problem-solving. The model first generates rationales in text form, followed by a computer program which executes to derive a numerical answer
To train the model, we needed a suitable problem set (the given “training set” of this competition is too small for fine-tuning) with “ground truth” solutions in ToRA format for supervised fine-tuning. Given the problem difficulty (comparable to AMC12 and AIME exams) and the special format (integer answers only), we used a combination of AMC, AIME, and Odyssey-Math as our problem set, removing multiple-choice options and filtering out problems with non-integer answers. This resulted in a dataset of 2,600 problems. We prompted GPT-4o (and DeepSeek-Coder-V2) with few-shot examples to generate 64 solutions for each problem, retaining those that led to correct answers. Our final dataset contained 41,160 problem-solution pairs. We performed supervised fine-tuning on the open-sourced DeepSeek-Math-7B-RL model for 3 epochs with a learning rate of 2e-5.
During inference, we employed the self-refinement technique (which is another widely adopted technique proposed by CMU!), providing feedback to the policy model on the execution results of the generated program (e.g., invalid output, execution failure) and allowing the model to refine the solution accordingly.
Below we present our ablation study on the techniques we employed for the policy model. We used the accuracy on a selected subset of the MATH test set as the evaluation metric. It’s easy to see the combination of techniques that lead to large performance gains compared with naive baselines.
| Model | Output format | Inference strategy | Accuracy |
|---|---|---|---|
| DeepSeek RL 7b | Text-only | Greedy decoding | 54.02% |
| DeepSeek RL 7b | ToRA | Greedy decoding | 58.05% |
| DeepSeek RL 7b | ToRA | Greedy + Self-refine | 60.73% |
| DeepSeek RL 7b | ToRA | Maj@16 + Self-refine | 70.46% |
| DeepSeek RL 7b | ToRA | Maj@64 + Self-refine | 72.48% |
| Our finetuned model | ToRA | Maj@16 + Self-refine | 74.50% |
| Our finetuned model | ToRA | Maj@64 + Self-refine | 76.51% |
Notably, the first-place team also used ToRA with self-refinement. However, they curated a much larger problem set of 60,000 problems and used GPT-4 to generate solutions in the ToRA format. Their dataset was more than 20x larger than ours. The cost to generate solutions was far beyond our budget as an academic team (over ![]() based on our estimation). Our problem set was based purely on publicly available data, and we spent only ~
based on our estimation). Our problem set was based purely on publicly available data, and we spent only ~![]() for solution generation.
for solution generation.
Reward model: Solution scorer using label-balance training
While the policy model was a creative problem solver, it could sometimes hallucinate and produce incorrect solutions. On the publicly available 10-problem training set, our policy model only correctly solved two problems using standard majority voting with 32 sampled solutions. Interestingly, for another 2 problems, the model generated correct solutions that failed to be selected due to wrong answers dominating in majority voting.
This observation highlighted the potential of the reward model. The reward model was a solution scorer that took the policy model’s output and generated a score between 0 and 1. Ideally, it assigned high scores to correct solutions and low scores to incorrect ones, aiding in the selection of correct answers during weighted majority voting.
The reward model was fine-tuned from a DeepSeek-Math-7B-RL model on a labeled dataset containing both correct and incorrect problem-solution pairs. We utilized the same problem set as for the policy model training and expanded it by incorporating problems from the MATH dataset with integer answers. Simple as it may sound, generating high-quality data and training a strong reward model was non-trivial. We considered the following two essential factors for the reward model training set:
- Label balance: The dataset should contain both correct (positive examples) and incorrect solutions (negative examples) for each problem, with a balanced number of correct and incorrect solutions.
- Diversity: The dataset should include diverse solutions for each problem, encompassing different correct approaches and various failure modes.
Sampling solutions from a single model cannot meet those factors. For example, while our fine-tuned policy model achieved very high accuracy on the problem set, it was unable to generate any incorrect solutions and lacked diversity amongst correct solutions. Conversely, sampling from a weaker model, such as DeepSeek-Math-7B-Base, rarely yielded correct solutions. To create a diverse set of models with varying capabilities, we employed two novel strategies:
- Interpolate between strong and weak models. For MATH problems, we interpolated the model parameters of a strong model (DeepSeek-Math-7B-RL) and a weak model (DeepSeek-Math-7B-Base) to get models with different level of capabilities. Denote by
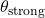 and
and 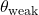 the model parameters of the strong and weak model. We considered interpolated models with parameters
the model parameters of the strong and weak model. We considered interpolated models with parameters 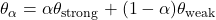 and set
and set 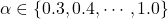 , obtaining 8 models. Those models exhibited different problem solving accuracies on MATH. We sampled two solutions from each model for each problem, yielding diverse outputs with balanced correct and incorrect solutions. This technique was motivated by the research on model parameter merging (e.g., model soups) and represented an interesting application of this idea, i.e., generating models with different levels of capabilities.
, obtaining 8 models. Those models exhibited different problem solving accuracies on MATH. We sampled two solutions from each model for each problem, yielding diverse outputs with balanced correct and incorrect solutions. This technique was motivated by the research on model parameter merging (e.g., model soups) and represented an interesting application of this idea, i.e., generating models with different levels of capabilities. - Leverage intermediate checkpoints. For the AMC, AIME, and Odyssey, recall that our policy model had been fine-tuned on those problems for 3 epochs. The final model and its intermediate checkpoints naturally provided us with multiple models exhibiting different levels of accuracy on these problems. We leveraged these intermediate checkpoints, sampling 12 solutions from each model trained for 0, 1, 2, and 3 epochs.
These strategies allowed us to obtain a diverse set of models almost for free, sampling varied correct and incorrect solutions. We further filtered the generated data by removing wrong solutions with non-integer answers since it was trivial to determine that those answers are incorrect during inference. In addition, for each problem, we maintained equal numbers of correct and incorrect solutions to ensure label balance and avoid a biased reward model. The final dataset contains 7000 unique problems and 37880 labeled problem-solution pairs. We finetuned DeepSeek-Math-7B-RL model for 2 epochs with learning rate 2e-5 on the curated dataset.

We validated the effectiveness of our reward model on the public training set. Notably, by pairing the policy model with the reward model and applying weighted majority voting, our method correctly solved 4 out of the 10 problems – while a single policy model could only solve 2 using standard majority voting.
Concluding remarks: Towards machine-based mathematical reasoning
With the models and techniques described above, our CMU-MATH team solved 22 out of 50 problems in the private test set, snagging the second place and establishing the best performance of an academic team. This outcome marks a significant step towards the goal of machine-based mathematical reasoning.
However, we also note that the accuracy achieved by our models still trails behind that of proficient human competitors who can easily solve over 95% of AIMO problems, indicating substantial room for improvement. There are a wide range of directions to be explored:
- Advanced inference-time algorithms for mathematical reasoning. Our dual-model approach is a robust technique to enhance model reasoning at inference time. Recent research from our team suggests that more advanced inference-time algorithms, e.g., tree search methods, could even surpass weighted majority voting. Although computational constraints limited our ability to deploy this technique in the AIMO competition, future explorations on optimizing these inference-time algorithms can potentially lead to better mathematical reasoning approaches.
- Integration of Automated Theorem Proving. Integrating automated theorem proving (ATP) tools, such as Lean, represents another promising frontier. ATP tools can provide rigorous logical frameworks and support for deeper mathematical analyses, potentially elevating the precision and reliability of problem-solving strategies employed by LLMs. The synergy between LLMs and ATP could lead to breakthroughs in complex problem-solving scenarios, where deep logical reasoning is essential.
- Leveraging Larger, More Diverse Datasets. The competition reinforced a crucial lesson about the pivotal role of data in machine learning. Rich, diverse datasets, especially those comprising challenging mathematical problems, are vital for training more capable models. We advocate for the creation and release of larger datasets focused on mathematical reasoning, which would not only benefit our research but also the broader AI and mathematics communities.
Finally, we would like to thank Kaggle and XTX Markets for organizing this wonderful competition. We have open-sourced our code and datasets used in our solution to ensure reproducibility and facilitate future research. We invite the community to explore, utilize, and build upon our work, which is available in our GitHub repository. For further details about our results, please feel free to reach out to us!
This article was initially published on the ML@CMU blog and appears here with the authors’ permission.
tags: deep dive








