
ΑΙhub.org
Bart Selman’s presidential address at #AAAI2022 – incomprehensible truths, fragile chains and hidden crystals

Every two years, the current AAAI president gives the opening address at the AAAI Conference on Artificial Intelligence. This year it was the turn of Bart Selman. In his talk he reviewed the current state of AI and presented examples of three different applications of AI to aid scientific discovery.
Bart began his talk by considering the deep-learning “revolution”, highlighting some of the areas that it has transformed, namely computer vision, natural language processing, machine translation, game play, and reinforcement learning. He noted that the field is undergoing a rapid acceleration at the moment, with an incredible rate of progress.
Another thing that excites him is what he sees as a reunification of the field. After years of specialization we are seeing the field come back together. Deep learning is being used to boost other areas of AI. This reunification allows us to return to some of the big open questions.
 Screenshot from Bart Selman’s talk.
Screenshot from Bart Selman’s talk.
An area of research focus for Bart concerns using AI methods to aid scientific discovery. In this plenary, he outlined three specific examples where AI has been used to accelerate scientific (and mathematical) progress.
1) Incomprehensible truths – Erdős discrepancy conjecture
The Erdős discrepancy conjecture states that “long sequences of +1s and -1s cannot be balanced”. If a sequence of +1s and -1s becomes long enough, it will necessarily become highly unbalanced. In this case, the definition of “balanced” considers not only the complete sequence, but also all of the subsequences (for example, creating new sequences by jumping every two, three, four, etc, numbers). To be balanced, the sum of not only the complete sequence, but also all of the subsequences, must be as close as possible to zero.
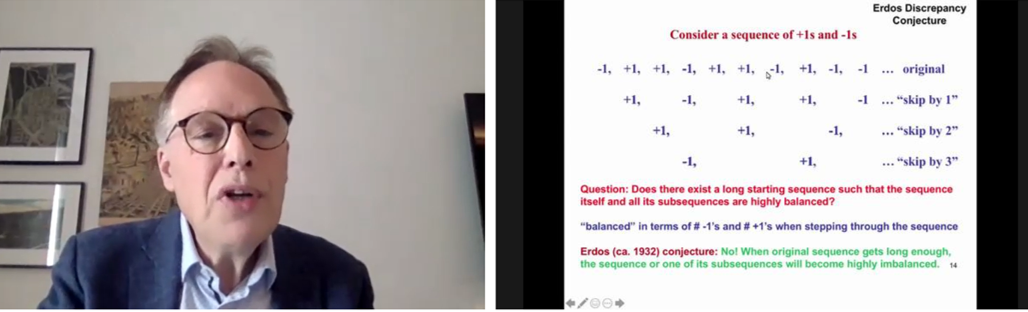 Explaining the Erdős discrepancy conjecture – what does it mean for a sequence to be balanced?
Explaining the Erdős discrepancy conjecture – what does it mean for a sequence to be balanced?
For many years, it was unknown how long you could make a sequence and still maintain a discrepancy (an imbalance) of two. It was only relatively recently (2014) that the discovery was made that there exists a sequence of length 1160 where the discrepancy remains at two. But, no balanced sequence (with a discrepany of two or fewer) of length 1161 or more exists. The link to AI comes from the fact that this problem was proved using a SAT solver paired with a very general reasoning method. The programme learnt new structure about the problem space in the midst of trying to solve the problem. As an output, the programme also produced a proof, of more than one billion reasoning steps.
Bart believes that the future for maths is that human maths will be augmented by machine-discovered mathematical truths.
2) Fragile chains – DeepSokoPlan
In this section of the talk, Bart considered whether we could discover mathematical proofs in more expressive formalisms. He described proofs like intricate plans, where every step needs to fit exactly with the previous step on the path to the goal.
To illustrate his point, Bart focussed on his work with Dieqiao Feng and Carla Gomes on Sokoban. Sokoban is a PSPACE-complete planning task and represents one of the hardest domains for current AI planners. It consists of a maze, and a character must push blocks onto specific squares within that maze.
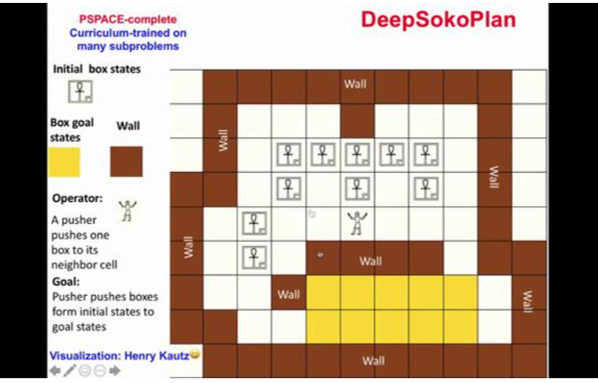
Their programme DeepSokoPlan combines data-driven deep reinforcement learning with knowledge-driven combinatorial reasoning. The aim is to find a solution to the Sokoban mazes. The maze pictured above is already beyond standard solvers and planners, which is why the combined approach they use is necessary. This method discovers both local and global strategies and combines them.
Bart’s prediction is that by scaling-up this method by two or three more orders of magnitude, there is the potential to use it for algorithmic discovery or general mathematical discovery. He stressed that we are still far from achieving this, but there is a possible path ahead.
3) Hidden crystals – bridging data and knowledge.
This final example concerned crystal structures. A longstanding problem in materials science has been inferring crystal structures from x-ray diffraction patterns. It would typically take researchers a year to decipher x-ray diffraction patterns to determine new structures. They would use prior knowledge of known crystal phases from other structures, and thermodynamic rules.
In contrast, by applying deep reasoning networks, the timescale for this work can be reduced to a matter of minutes. The network takes in the x-ray diffraction patterns and combines deep-learning with reasoning about known phases and thermodynamic rules to output crystal structures. This is all done without training data.
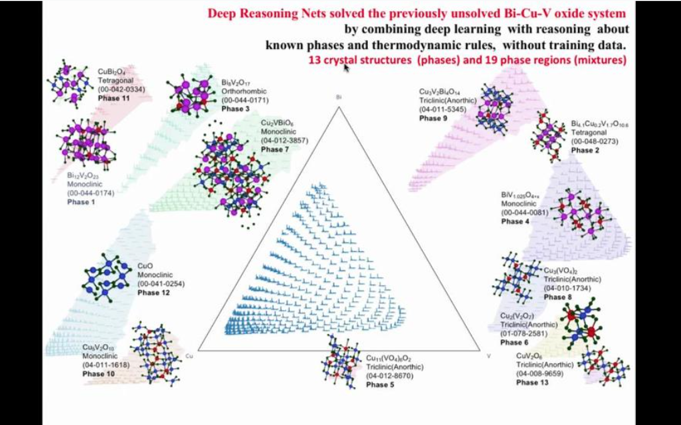
What Bart finds exciting about this method is that it combines data (measurements) with prior knowledge of crystal structures and materials physics, which is very much what a human scientist does.
To close his talk, Bart encouraged the audience to read the 20 year roadmap for AI, which he compiled, along with past AAAI president Yolanda Gil, and the help of over 100 AI researchers. As part of this roadmap, they identified areas where they believed AI could have significant impact in the coming years.
You can watch the talk in full here.
tags: AAAI, AAAI2022










